2.1 勾股定理(苏科版数学八年级上学期)[上学期]
文档属性
| 名称 | 2.1 勾股定理(苏科版数学八年级上学期)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 567.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-01-06 00:00:00 | ||
图片预览







文档简介
课件21张PPT。勾股定理ICM2002 荷花问题平平湖水清可鉴,荷花半尺出水面。
忽来一阵狂风急,吹倒荷花水中偃。
湖面之上不复见,入秋渔翁始发现。
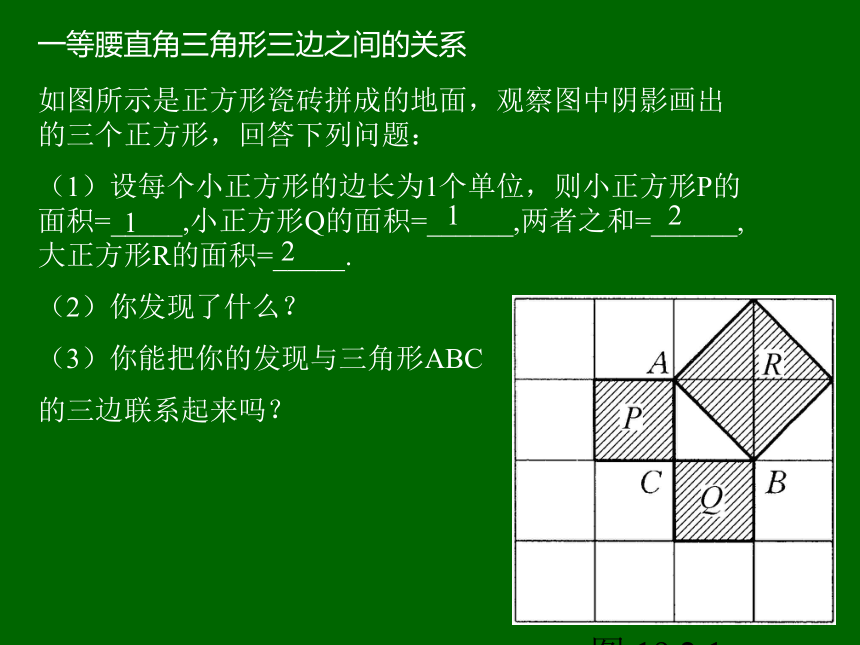
残花离根二尺远,试问水深尺若干。聪明的同学们,你能就此画出示意图吗?如图所示是正方形瓷砖拼成的地面,观察图中阴影画出的三个正方形,回答下列问题:
(1)设每个小正方形的边长为1个单位,则小正方形P的面积=_____,小正方形Q的面积=______,两者之和=______,大正方形R的面积=_____.
(2)你发现了什么?
(3)你能把你的发现与三角形ABC
的三边联系起来吗?1122一等腰直角三角形三边之间的关系二 试一试
观察下图,如果每一小方格表示1平方厘米,把观察到的结果填空:
(1)正方形P的面积=_______平方厘米;
正方形Q的面积=_______平方厘米;
正方形R的面积=_______平方厘米;
(2) 正方形P,Q,R的面积之间的关系
是_____________;
(3)由此得到Rt△ABC的三边的长度之间
存在关系__________.91625SP+SQ=SR(任意直角三角形三边的关系)三 做一做:
在草稿本上,用三角尺画出两条直角边分别为5cm,12cm的直角三角形,然后用刻度尺量出斜边的长,并验证上述关系对这个直角三角形是否成立.两条直角边的长为6cm和8cm呢?同学们,你们发现了什么结论吗 对于任意的直角三角形,如果把它的两条直角边分别为a,b,斜边为c,那么一定有
勾股定理 直角三角形两直角边的平方和等于斜边的平方四 大话勾股定理早在公元前11世纪的西周初期,数学家商高曾与辅佐周成王的周公谈到直角三角形具有这样的一个性质:如果直角三角形的两个直角边分别为3和4,则这个直角三角形的斜边为5。利用商高的方法,很容易得到更一般的结论:在直角三角形中,两条直角边的平方和等于斜边的平方。这就是勾股定理或商高定理,西方称之为毕达哥拉斯定理。 勾股定理是一条古老而又应用十分广泛的定理。例如从勾股定理出发逐渐发展了开平方、开立方;用勾股定理求圆周率。据说4000多年前,中国的大禹曾在治理洪水的过程中利用勾股定理来测量两地的地势差。勾股定理以其简单、优美的形式,丰富、深刻的内容,充分反映了自然界的和谐关系。人们对勾股定理一直保持着极高的热情,仅定理的证明就多达几十种,甚至著名的大物理学家爱因斯坦也给出了一个证明。中国著名数学家华罗庚在谈论到一旦人类遇到了“外星人”,该怎样与他们交谈时,曾建议用一幅反映勾股定理的数形关系图来作为与“外星人”交谈的语言。这充分说明了勾股定理是自然界最本质、最基本的规律之一,而在对这样一个重要规律的发现和应用上,中国人走在了前面。 自豪!例1 如图,将长为5.41米的 梯子AC斜靠在墙上,BC长为2.16米,求梯子上端A到墙的底端B的距离AB.(精确到0.01米)ABC动脑想一想,看谁反应快!!
1.在Rt△ABC中,AB=c,BC=a,AC=b, ∠C=90°,
(1)已知a=3,b=4,则c=_______;
(2)已知a=6,c=10,则b=_____;
(3)已知a=5,b=8,则c=______.
2.已知Rt△ABC中,∠B= 90°,AC= ,BC=
则AB=———, ∠A=——
3.在平面直角坐标系中,点(-3,-4)与原点之间的
距离是——,点(3,- 4)与点(2,1)之间的距
离是——4.如图是 一大厦的柱子,它是圆柱形的 ,它的高是8米,底面半径是2米,一只壁虎在A点,想要吃到B点的昆虫,它爬行的最短距离 是多少?(圆周率取3)
AB5 如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长有多长??183024同学们,这一节课你感到自己有什么收获呢? 小结作业:
P104 2 P120 12THE END勾三股四弦五夏禹治水赵爽的 勾股圆方图一九五五年希腊发行的邮票
忽来一阵狂风急,吹倒荷花水中偃。
湖面之上不复见,入秋渔翁始发现。
残花离根二尺远,试问水深尺若干。聪明的同学们,你能就此画出示意图吗?如图所示是正方形瓷砖拼成的地面,观察图中阴影画出的三个正方形,回答下列问题:
(1)设每个小正方形的边长为1个单位,则小正方形P的面积=_____,小正方形Q的面积=______,两者之和=______,大正方形R的面积=_____.
(2)你发现了什么?
(3)你能把你的发现与三角形ABC
的三边联系起来吗?1122一等腰直角三角形三边之间的关系二 试一试
观察下图,如果每一小方格表示1平方厘米,把观察到的结果填空:
(1)正方形P的面积=_______平方厘米;
正方形Q的面积=_______平方厘米;
正方形R的面积=_______平方厘米;
(2) 正方形P,Q,R的面积之间的关系
是_____________;
(3)由此得到Rt△ABC的三边的长度之间
存在关系__________.91625SP+SQ=SR(任意直角三角形三边的关系)三 做一做:
在草稿本上,用三角尺画出两条直角边分别为5cm,12cm的直角三角形,然后用刻度尺量出斜边的长,并验证上述关系对这个直角三角形是否成立.两条直角边的长为6cm和8cm呢?同学们,你们发现了什么结论吗 对于任意的直角三角形,如果把它的两条直角边分别为a,b,斜边为c,那么一定有
勾股定理 直角三角形两直角边的平方和等于斜边的平方四 大话勾股定理早在公元前11世纪的西周初期,数学家商高曾与辅佐周成王的周公谈到直角三角形具有这样的一个性质:如果直角三角形的两个直角边分别为3和4,则这个直角三角形的斜边为5。利用商高的方法,很容易得到更一般的结论:在直角三角形中,两条直角边的平方和等于斜边的平方。这就是勾股定理或商高定理,西方称之为毕达哥拉斯定理。 勾股定理是一条古老而又应用十分广泛的定理。例如从勾股定理出发逐渐发展了开平方、开立方;用勾股定理求圆周率。据说4000多年前,中国的大禹曾在治理洪水的过程中利用勾股定理来测量两地的地势差。勾股定理以其简单、优美的形式,丰富、深刻的内容,充分反映了自然界的和谐关系。人们对勾股定理一直保持着极高的热情,仅定理的证明就多达几十种,甚至著名的大物理学家爱因斯坦也给出了一个证明。中国著名数学家华罗庚在谈论到一旦人类遇到了“外星人”,该怎样与他们交谈时,曾建议用一幅反映勾股定理的数形关系图来作为与“外星人”交谈的语言。这充分说明了勾股定理是自然界最本质、最基本的规律之一,而在对这样一个重要规律的发现和应用上,中国人走在了前面。 自豪!例1 如图,将长为5.41米的 梯子AC斜靠在墙上,BC长为2.16米,求梯子上端A到墙的底端B的距离AB.(精确到0.01米)ABC动脑想一想,看谁反应快!!
1.在Rt△ABC中,AB=c,BC=a,AC=b, ∠C=90°,
(1)已知a=3,b=4,则c=_______;
(2)已知a=6,c=10,则b=_____;
(3)已知a=5,b=8,则c=______.
2.已知Rt△ABC中,∠B= 90°,AC= ,BC=
则AB=———, ∠A=——
3.在平面直角坐标系中,点(-3,-4)与原点之间的
距离是——,点(3,- 4)与点(2,1)之间的距
离是——4.如图是 一大厦的柱子,它是圆柱形的 ,它的高是8米,底面半径是2米,一只壁虎在A点,想要吃到B点的昆虫,它爬行的最短距离 是多少?(圆周率取3)
AB5 如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长有多长??183024同学们,这一节课你感到自己有什么收获呢? 小结作业:
P104 2 P120 12THE END勾三股四弦五夏禹治水赵爽的 勾股圆方图一九五五年希腊发行的邮票
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
