3.1 用表格表示的变量间的关系课件(共24张PPT) 北师大版数学七年级下册
文档属性
| 名称 | 3.1 用表格表示的变量间的关系课件(共24张PPT) 北师大版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 587.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-16 13:46:49 | ||
图片预览








文档简介
(共24张PPT)
3.1用表格表示的变量间关系
在具体情境中理解什么是变量、自变量、因变量.
01
02
03
学习目标
能从表格中获得变量之间关系的信息,能用表格表示变量之间的关系,尝试对变化趋势进行初步的预测.
经历观察、实验、猜想、验证等数学活动,发展合理推理能力,并能有条理地、清晰地阐述自己的观点.
理解什么是变量、自变量、因变量.
能用表格表示变量之间的关系,尝试对变化趋势进行初步的预测.
重点:
难点:
学习重难点
情景导入
你的睡眠时间充足吗?
根据科学研究表明,一个10岁至50岁的人每天所需睡眠时间(H小时)可用公式
H=(110-N)/10计算出来,其中N代表这个人的岁数,请赶紧算算你所需的睡眠时间吧!
会变化的量是:
不会变的量是:
H和N.
110和10.
预习检测
1. 学校计划买100个乒乓球,买乒乓球的总费用w(元)与单价n(元/个)的关系式w=100n中,( )
A. 100是常量,w,n是变量 B. 100,w是常量,n是变量
C. 100,n是常量,w是变量 D. 无法确定
2. 某河受暴雨袭击,一天的水位记录如下表.观察表中数据,水位上升最快的时段是( )
A. 8~12时 B.12~16时 C.16~20时 D. 20~24时
A
D
探究新知
小车下滑实验
探究新知
细心体会哦!
20
0
40
60
80
100
单位:cm
探究新知
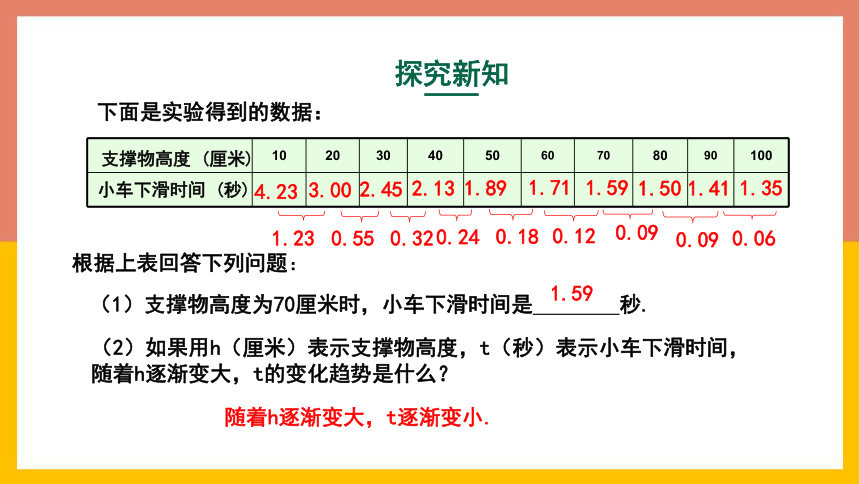
下面是实验得到的数据:
10 20 30 40 50 60 70 80 90 100
(1)支撑物高度为70厘米时,小车下滑时间是 秒.
(2)如果用h(厘米)表示支撑物高度,t(秒)表示小车下滑时间,随着h逐渐变大,t的变化趋势是什么?
4.23
1.35
1.41
1.50
1.59
1.71
1.89
2.13
2.45
3.00
根据上表回答下列问题:
1.23
0.55
0.32
0.24
0.18
0.12
0.09
0.09
0.06
1.59
随着h逐渐变大,t逐渐变小.
支撑物高度 (厘米)
小车下滑时间 (秒)
探究新知
(3)h每增加10厘米,t的变化情况相同吗?
(4)估计当h=110厘米时,t的值是多少?你是怎样估计的?
t的变化越来越小
1.35秒到1.29秒中的任一值
归纳
在前面的表格中,支撑物高度h和小车下滑时间t都在变化,它们都是变量.其中t随h的变化而变化,h是自变量,t是因变量.
在这一变化过程中,小车下滑的距离(木板长度)一直没有变化.像这种在变化过程中数值始终不变的量叫做常量.
典例精析
【例1】某电动车厂2014年各月份生产电动车的数量情况如下表:
(1)为什么称电动车的月产量y为因变量?它是谁的因变量?
时间x/月 1 2 3 4 5 6 7 8 9 10 11 12
月产量y/万辆 8 8.5 9 10 11 12 10 9.5 9 10 10 10.5
(1)电动车的月产量y为随着时间的变化而变化,有一个时间就有唯一一个y,月产量是时间的因变量;
典例精析
(2)哪个月份电动车的产量最高?哪个月份电动车的产量最低?
(3)哪两个月份之间产量相差最大?根据这两个月的产量,电动车厂的厂长应该怎么做?
(2)六月份产量最高,一月份产量最低;
(3)六月份和一月份相差最大,在一月份加紧生产,实现产量的增值.
练一练
骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化.在这一问题中,自变量是( )
A.沙漠 B.体温 C.时间 D.骆驼
C
典例精析
【例2】某布行购进了一批花布,销售的数量与销售收入之间的关系如下:
(1)如果用x表示花布的销售数量,y表示花布的销售收入,随着x的逐渐变大,y的变化趋势是____________.
(2)在这个变化过程中,自变量是________,因变量是________.
(3)当花布销售数量由2米变到6米时,花布销售收入由_____元变到_____元.
销售数量(米) 1 2 3 4 5 6
销售收入(元) 8.3 16.6 24.9 33.2 41.5 49.8
逐渐变大
销售数量
销售收入
16.6
49.8
练一练
研究表明,当钾肥和磷肥的施用量一定时,土豆的产量与氮肥的施用量有如下关系:
氮肥施用量/(千克/公顷) 0 34 67 101 135 202 259 336 404
471
土豆产量/(吨/公顷) 15.18 21.36 25.72 32.29 34.03 39.45 43.15 43.46 40.83
30.75
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当氮肥的施用量是101千克/公顷时,土豆的产量是多少?如果不施氮肥呢?
(3)根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说说你的理由.
(4)粗略说一说氮肥的施用量对土豆产量的影响.
练一练
练一练
解:(1)上表反映了土豆的产量与氮肥的施用量两个变量之间的关系,氮肥的施用量是自变量,土豆的产量是因变量.
(2)当氮肥的施用量是101千克/公顷时,土豆的产量是32.29吨/公顷,如果不施氮肥土豆的产量是15.18吨/公顷.
(4)当氮肥的施用量不大于336千克/公顷时,随着氮肥施用量的增加,土豆的产量增加,当氮肥的施用量大于336千克/公顷时,随着氮肥施用量的增加,土豆的产量反而减小.
(3)当氮肥的施用量是336千克/公顷时最为适宜,此时土豆产量最高.
练一练
课堂练习
1.“一石激起千层浪”,一块石头被投入水中,会在水面上激起一圈圈圆形的涟漪,在这个过程中,自变量是( )
A.时间 B.圆的面积 C.圆的半径 D.石头
C
2.从空中落下一个物体,它降落的速度随时间的变化而变化,即落地前速度随时间的增大而逐渐增大,这个问题中自变量是 ( )
A.物体 B.速度 C.时间 D.空气
C
课堂练习
3.对于圆的周长公式C=2πR,下列说法正确的是( )
A.π,R是变量,2是常量
B.R是变量,π是常量
C.C是变量,π,R是常量
D.C,R是变量,2,π是常量
D
4.婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,以上叙述中,_____________发生变化,自变量是________,因变量是________.
年龄和体重
年龄
体重
课堂练习
5.父亲告诉小明:“距离地面越远,温度越低”,并且出示了下面的表格:
据表,父亲还给小明出了下面几个问题,请你和小明一起回答:
(1)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t如何变化?
(2)你知道距离地面5千米的高空温度是多少吗?
(3)你能预测出距离地面6千米的高空温度是多少吗?
距离地面高度(千米) 0 1 2 3 4 5
温度(℃) 20 14 8 2 -4 -10
课堂练习
解:(1)根据表格数据,距离地面越远,温度越低,所以随着h的升高,t在降低.
(2)根据表格,高度是5千米时的温度是-10 ℃.
(3)根据规律,高度每升高1千米,温度降低6 ℃,所以距离地面6千米时的温度是-10-6=-16(℃) .
课堂练习
6.收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值:
(3)在这个问题中,哪些量是变量?哪些量是常量?
波长l(m) 300 500 600 1000 1500
频率f(khz) 1000 600 500 300 200
l 与 f 的乘积是一个定值,即lf=300 000,
越小
变量是:波长、频率,常量是:300 000
观察上表回答:
(1)波长l和和频率f之间有什么关系
(2)波长l越越大,频率f就______.
总结
提示:在变化过程中起主导作用的那个变量是自变量.
名称 概念
变化中的量 自变量 自主变化的量
因变量 随_______变化而变化的量
常量 变化过程中数值_________的量
变量之间关系的表示 表格法 利用表格表示_______和_______之间的关系
自变量
始终不变
自变量
因变量
3.1用表格表示的变量间关系
在具体情境中理解什么是变量、自变量、因变量.
01
02
03
学习目标
能从表格中获得变量之间关系的信息,能用表格表示变量之间的关系,尝试对变化趋势进行初步的预测.
经历观察、实验、猜想、验证等数学活动,发展合理推理能力,并能有条理地、清晰地阐述自己的观点.
理解什么是变量、自变量、因变量.
能用表格表示变量之间的关系,尝试对变化趋势进行初步的预测.
重点:
难点:
学习重难点
情景导入
你的睡眠时间充足吗?
根据科学研究表明,一个10岁至50岁的人每天所需睡眠时间(H小时)可用公式
H=(110-N)/10计算出来,其中N代表这个人的岁数,请赶紧算算你所需的睡眠时间吧!
会变化的量是:
不会变的量是:
H和N.
110和10.
预习检测
1. 学校计划买100个乒乓球,买乒乓球的总费用w(元)与单价n(元/个)的关系式w=100n中,( )
A. 100是常量,w,n是变量 B. 100,w是常量,n是变量
C. 100,n是常量,w是变量 D. 无法确定
2. 某河受暴雨袭击,一天的水位记录如下表.观察表中数据,水位上升最快的时段是( )
A. 8~12时 B.12~16时 C.16~20时 D. 20~24时
A
D
探究新知
小车下滑实验
探究新知
细心体会哦!
20
0
40
60
80
100
单位:cm
探究新知
下面是实验得到的数据:
10 20 30 40 50 60 70 80 90 100
(1)支撑物高度为70厘米时,小车下滑时间是 秒.
(2)如果用h(厘米)表示支撑物高度,t(秒)表示小车下滑时间,随着h逐渐变大,t的变化趋势是什么?
4.23
1.35
1.41
1.50
1.59
1.71
1.89
2.13
2.45
3.00
根据上表回答下列问题:
1.23
0.55
0.32
0.24
0.18
0.12
0.09
0.09
0.06
1.59
随着h逐渐变大,t逐渐变小.
支撑物高度 (厘米)
小车下滑时间 (秒)
探究新知
(3)h每增加10厘米,t的变化情况相同吗?
(4)估计当h=110厘米时,t的值是多少?你是怎样估计的?
t的变化越来越小
1.35秒到1.29秒中的任一值
归纳
在前面的表格中,支撑物高度h和小车下滑时间t都在变化,它们都是变量.其中t随h的变化而变化,h是自变量,t是因变量.
在这一变化过程中,小车下滑的距离(木板长度)一直没有变化.像这种在变化过程中数值始终不变的量叫做常量.
典例精析
【例1】某电动车厂2014年各月份生产电动车的数量情况如下表:
(1)为什么称电动车的月产量y为因变量?它是谁的因变量?
时间x/月 1 2 3 4 5 6 7 8 9 10 11 12
月产量y/万辆 8 8.5 9 10 11 12 10 9.5 9 10 10 10.5
(1)电动车的月产量y为随着时间的变化而变化,有一个时间就有唯一一个y,月产量是时间的因变量;
典例精析
(2)哪个月份电动车的产量最高?哪个月份电动车的产量最低?
(3)哪两个月份之间产量相差最大?根据这两个月的产量,电动车厂的厂长应该怎么做?
(2)六月份产量最高,一月份产量最低;
(3)六月份和一月份相差最大,在一月份加紧生产,实现产量的增值.
练一练
骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化.在这一问题中,自变量是( )
A.沙漠 B.体温 C.时间 D.骆驼
C
典例精析
【例2】某布行购进了一批花布,销售的数量与销售收入之间的关系如下:
(1)如果用x表示花布的销售数量,y表示花布的销售收入,随着x的逐渐变大,y的变化趋势是____________.
(2)在这个变化过程中,自变量是________,因变量是________.
(3)当花布销售数量由2米变到6米时,花布销售收入由_____元变到_____元.
销售数量(米) 1 2 3 4 5 6
销售收入(元) 8.3 16.6 24.9 33.2 41.5 49.8
逐渐变大
销售数量
销售收入
16.6
49.8
练一练
研究表明,当钾肥和磷肥的施用量一定时,土豆的产量与氮肥的施用量有如下关系:
氮肥施用量/(千克/公顷) 0 34 67 101 135 202 259 336 404
471
土豆产量/(吨/公顷) 15.18 21.36 25.72 32.29 34.03 39.45 43.15 43.46 40.83
30.75
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当氮肥的施用量是101千克/公顷时,土豆的产量是多少?如果不施氮肥呢?
(3)根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说说你的理由.
(4)粗略说一说氮肥的施用量对土豆产量的影响.
练一练
练一练
解:(1)上表反映了土豆的产量与氮肥的施用量两个变量之间的关系,氮肥的施用量是自变量,土豆的产量是因变量.
(2)当氮肥的施用量是101千克/公顷时,土豆的产量是32.29吨/公顷,如果不施氮肥土豆的产量是15.18吨/公顷.
(4)当氮肥的施用量不大于336千克/公顷时,随着氮肥施用量的增加,土豆的产量增加,当氮肥的施用量大于336千克/公顷时,随着氮肥施用量的增加,土豆的产量反而减小.
(3)当氮肥的施用量是336千克/公顷时最为适宜,此时土豆产量最高.
练一练
课堂练习
1.“一石激起千层浪”,一块石头被投入水中,会在水面上激起一圈圈圆形的涟漪,在这个过程中,自变量是( )
A.时间 B.圆的面积 C.圆的半径 D.石头
C
2.从空中落下一个物体,它降落的速度随时间的变化而变化,即落地前速度随时间的增大而逐渐增大,这个问题中自变量是 ( )
A.物体 B.速度 C.时间 D.空气
C
课堂练习
3.对于圆的周长公式C=2πR,下列说法正确的是( )
A.π,R是变量,2是常量
B.R是变量,π是常量
C.C是变量,π,R是常量
D.C,R是变量,2,π是常量
D
4.婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,以上叙述中,_____________发生变化,自变量是________,因变量是________.
年龄和体重
年龄
体重
课堂练习
5.父亲告诉小明:“距离地面越远,温度越低”,并且出示了下面的表格:
据表,父亲还给小明出了下面几个问题,请你和小明一起回答:
(1)如果用h表示距离地面的高度,用t表示温度,那么随着h的变化,t如何变化?
(2)你知道距离地面5千米的高空温度是多少吗?
(3)你能预测出距离地面6千米的高空温度是多少吗?
距离地面高度(千米) 0 1 2 3 4 5
温度(℃) 20 14 8 2 -4 -10
课堂练习
解:(1)根据表格数据,距离地面越远,温度越低,所以随着h的升高,t在降低.
(2)根据表格,高度是5千米时的温度是-10 ℃.
(3)根据规律,高度每升高1千米,温度降低6 ℃,所以距离地面6千米时的温度是-10-6=-16(℃) .
课堂练习
6.收音机刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值:
(3)在这个问题中,哪些量是变量?哪些量是常量?
波长l(m) 300 500 600 1000 1500
频率f(khz) 1000 600 500 300 200
l 与 f 的乘积是一个定值,即lf=300 000,
越小
变量是:波长、频率,常量是:300 000
观察上表回答:
(1)波长l和和频率f之间有什么关系
(2)波长l越越大,频率f就______.
总结
提示:在变化过程中起主导作用的那个变量是自变量.
名称 概念
变化中的量 自变量 自主变化的量
因变量 随_______变化而变化的量
常量 变化过程中数值_________的量
变量之间关系的表示 表格法 利用表格表示_______和_______之间的关系
自变量
始终不变
自变量
因变量
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
