4.3.2 探索三角形全等的条件课件(共24张PPT) 北师大版数学七年级下册
文档属性
| 名称 | 4.3.2 探索三角形全等的条件课件(共24张PPT) 北师大版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 429.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-16 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
4.3.2探索三角形全等的条件
探索并正确理解三角形全等的条件“ASA”和“AAS”.
01
02
03
学习目标
会用三角形全等的条件“ASA”和“AAS”说明两个三角形全等.
在探索三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单的推理.
探索并正确理解三角形全等的条件“ASA”和“AAS”.
会用三角形全等的条件“ASA”和“AAS”说明两个三角形全等.
重点:
难点:
学习重难点
温故知新
1.全等三角形的性质: ;
2.三角形全等的条件: .
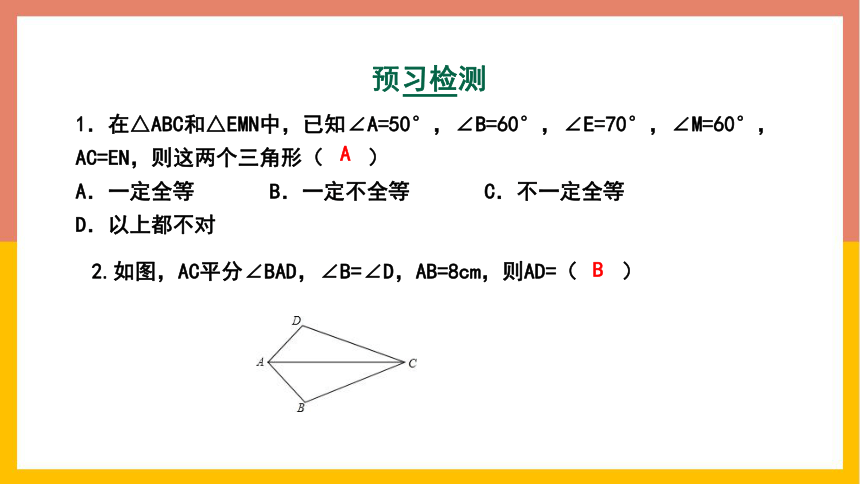
1.在△ABC和△EMN中,已知∠A=50°,∠B=60°,∠E=70°,∠M=60°,AC=EN,则这两个三角形( )
A.一定全等 B.一定不全等 C.不一定全等
D.以上都不对
2.如图,AC平分∠BAD,∠B=∠D,AB=8cm,则AD=( )
预习检测
A
B
情景导入
一张教学用的三角形硬纸板不小心被撕坏了,如图,你能制作一张与原来同样大小的新教具?能恢复三角形的原貌吗?
怎么办?可以帮帮我吗?
探究新知
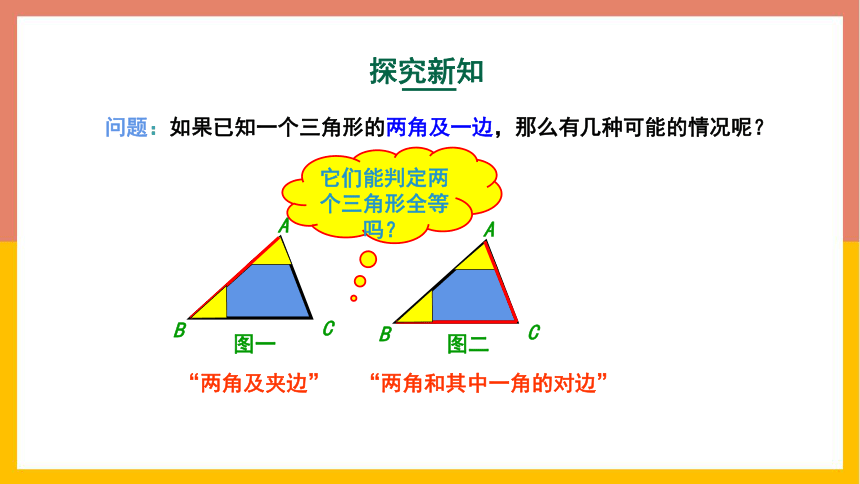
问题:如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
A
B
C
图一
图二
“两角及夹边”
“两角和其中一角的对边”
它们能判定两个三角形全等吗?
想一想
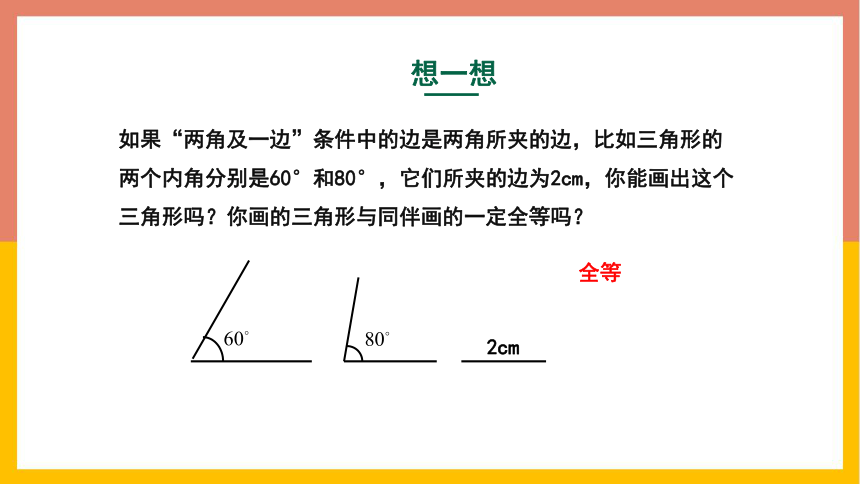
如果“两角及一边”条件中的边是两角所夹的边,比如三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗?
2cm
全等
探究新知
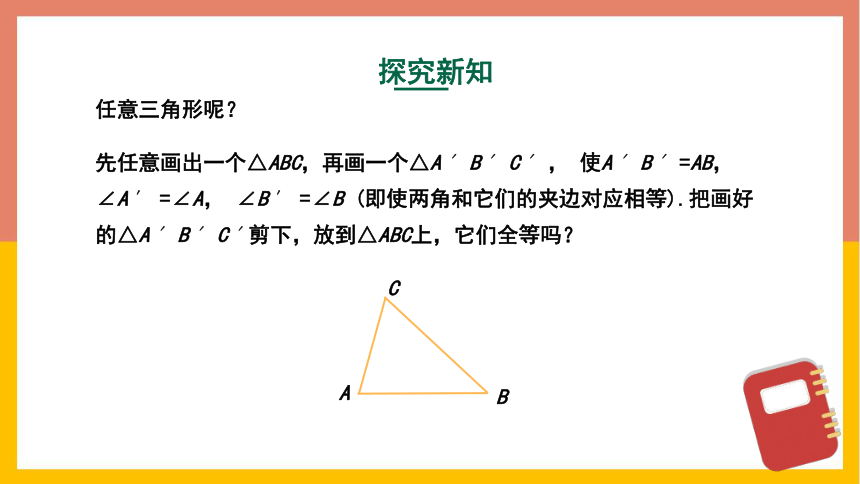
先任意画出一个△ABC,再画一个△A ′ B ′ C ′ , 使A ′ B ′ =AB, ∠A ′ =∠A, ∠B ′ =∠B (即使两角和它们的夹边对应相等).把画好的△A ′ B ′ C ′剪下,放到△ABC上,它们全等吗?
A
C
B
任意三角形呢?
做一做
A
C
B
C′
E
D
作法:
(1)画A'B'=AB;
(2)在A'B'的同旁画∠DA'B '=∠A,∠EB'A '=∠B,A'D,B'E相交于点C'.
想一想:从中你能发现什么规律?
A′
B′
归纳总结
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
书写格式:
∠A=∠A′ (已知),
AB=A′ B′ (已知),
∠B=∠B′ (已知),
在△ABC和△A′ B′ C′中,
所以 △ABC≌△ A′ B′ C′ (ASA).
A
B
C
A ′
B ′
C ′
想一想
如图所示,AB 与CD 相交于点O,O 是 AB 的中点,∠A = ∠B,△AOC 与△BOD 全等吗?为什么?
解:因为点O 是AB的中点,
所以OA = OB.
又已知∠A = ∠B,且∠AOC = ∠BOD,
所以△AOC ≌ △BOD.
典例精析
【例】 已知:∠ABC=∠DCB,∠ACB= ∠DBC,试说明:△ABC≌△DCB.
∠ABC=∠DCB(已知),
BC=CB(公共边),
∠ACB=∠DBC(已知),
解:
在△ABC和△DCB中,
所以△ABC≌△DCB(ASA ).
B
C
A
D
变式训练
如图,已知点E,C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F.试说明:△ABC≌△DEF.
解:因为AB∥DE,
所以∠B=∠DEF,
因为BE=CF,
所以BC=EF.
因为∠ACB=∠F,
所以△ABC≌△DEF .(ASA )
A
B
D
F
E
C
探究新知
如果“两角及一边”条件中的边是其中一角的对边,情况会怎样呢?你能将它转化为具体的条件吗?
若三角形的两个内角分别是60°和40°,且40°所对的边为2cm,你能画出这个三角形吗
60°
40°
2cm
想一想
60°
40°
这里的条件与“做一做”中的条件有什么相同点与不同点?你能将它转化为“做一做”中的条件吗?
归纳总结
∠A=∠A′(已知),
∠B=∠B′ (已知),
AC=A′C ′(已知),
在△ABC和△A′B′C′中,
所以 △ABC≌△ A′ B′ C′(AAS).
A
B
C
A ′
B ′
C ′
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成 “角角边”或“AAS ” .
书写格式:
典例精析
【例】 在△ABC和△DEF中,∠A=∠D,∠B= ∠E,BC=EF.试说明:AC=DF.
解:
所以△ABC≌△DEF(AAS ).
∠A=∠D,
∠B=∠E.
BC=EF.
在△ABC和△DEF中,
所以AC = DF.
实战演练
如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E.试说明:△BDA≌△AEC .
解:因为BD⊥m,CE⊥m,所以∠ADB=∠CEA=90°,
所以∠ABD+∠BAD=90°.
因为AB⊥AC,
所以∠BAD+∠CAE=90°,
∠ABD=∠CAE.
在△BDA和△AEC中,
∠ADB=∠CEA=90°,
∠ABD=∠CAE,
AB=AC,
所以△BDA≌△AEC(AAS).
课堂练习
1. 在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°∠C′=69° ,∠A′=44°,且AC=A′C′,那么这两个三角形( )
A.一定不全等 B.一定全等 C.不一定全等 D.以上都不对
B
2.如图,已知在△ABD和△ABC中,∠DAB=∠CAB,点A,B,E在同一条直线上,若使△ABD≌△ABC,则还需添加的一个条件是_________________________.(只填一个即可)
∠D=∠C或∠ABD=∠ABC等
课堂练习
3.如图,已知:AD为△ABC的中线,且CF⊥AD于点F,BE⊥AD交AD的延长线于点E.试说明:BE=CF.
解:因为AD为△ABC的中线,
所以BD=CD.因为BE⊥AD,CF⊥AD,
所以∠BED=∠CFD=90°.
在△BED与△CFD中,
所以△BED≌△CFD(AAS).所以BE=CF.
课堂练习
4.如图,点D在AB上,点E在AC上,AB=AC, ∠B=∠C,试说明:AD=AE.
A
B
C
D
E
解:在△ACD和△ABE中,
∠A=∠A(公共角 ),
AC=AB(已知),
∠C=∠B (已知 ),
所以 △ACD≌△ABE(ASA),
所以AD=AE.
课堂练习
5.已知:如图, AB⊥BC,AD⊥DC,∠1=∠2, 试说明:AB=AD.
A
C
D
B
1
2
解: 因为 AB⊥BC,AD⊥DC,
所以 ∠ B=∠D=90 °.
在△ABC和△ADC中,
∠1=∠2 (已知),
∠ B=∠D(已证),
AC=AC (公共边),
所以△ABC≌△ADC(AAS),
所以AB=AD.
总结
角边角和
角角边
内容
有两角及夹边对应相等的两个三角形全等(简写成 “ASA”)
应用
为证明线段和角相等提供了新的证法
注意
注意“角角边”、“角边角”中两角与边的区别
两角分别相等且其中一组等角的对边相等的两个三角形全等,(简写成 “AAS ” )
内容
4.3.2探索三角形全等的条件
探索并正确理解三角形全等的条件“ASA”和“AAS”.
01
02
03
学习目标
会用三角形全等的条件“ASA”和“AAS”说明两个三角形全等.
在探索三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单的推理.
探索并正确理解三角形全等的条件“ASA”和“AAS”.
会用三角形全等的条件“ASA”和“AAS”说明两个三角形全等.
重点:
难点:
学习重难点
温故知新
1.全等三角形的性质: ;
2.三角形全等的条件: .
1.在△ABC和△EMN中,已知∠A=50°,∠B=60°,∠E=70°,∠M=60°,AC=EN,则这两个三角形( )
A.一定全等 B.一定不全等 C.不一定全等
D.以上都不对
2.如图,AC平分∠BAD,∠B=∠D,AB=8cm,则AD=( )
预习检测
A
B
情景导入
一张教学用的三角形硬纸板不小心被撕坏了,如图,你能制作一张与原来同样大小的新教具?能恢复三角形的原貌吗?
怎么办?可以帮帮我吗?
探究新知
问题:如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
A
B
C
图一
图二
“两角及夹边”
“两角和其中一角的对边”
它们能判定两个三角形全等吗?
想一想
如果“两角及一边”条件中的边是两角所夹的边,比如三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗?
2cm
全等
探究新知
先任意画出一个△ABC,再画一个△A ′ B ′ C ′ , 使A ′ B ′ =AB, ∠A ′ =∠A, ∠B ′ =∠B (即使两角和它们的夹边对应相等).把画好的△A ′ B ′ C ′剪下,放到△ABC上,它们全等吗?
A
C
B
任意三角形呢?
做一做
A
C
B
C′
E
D
作法:
(1)画A'B'=AB;
(2)在A'B'的同旁画∠DA'B '=∠A,∠EB'A '=∠B,A'D,B'E相交于点C'.
想一想:从中你能发现什么规律?
A′
B′
归纳总结
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
书写格式:
∠A=∠A′ (已知),
AB=A′ B′ (已知),
∠B=∠B′ (已知),
在△ABC和△A′ B′ C′中,
所以 △ABC≌△ A′ B′ C′ (ASA).
A
B
C
A ′
B ′
C ′
想一想
如图所示,AB 与CD 相交于点O,O 是 AB 的中点,∠A = ∠B,△AOC 与△BOD 全等吗?为什么?
解:因为点O 是AB的中点,
所以OA = OB.
又已知∠A = ∠B,且∠AOC = ∠BOD,
所以△AOC ≌ △BOD.
典例精析
【例】 已知:∠ABC=∠DCB,∠ACB= ∠DBC,试说明:△ABC≌△DCB.
∠ABC=∠DCB(已知),
BC=CB(公共边),
∠ACB=∠DBC(已知),
解:
在△ABC和△DCB中,
所以△ABC≌△DCB(ASA ).
B
C
A
D
变式训练
如图,已知点E,C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F.试说明:△ABC≌△DEF.
解:因为AB∥DE,
所以∠B=∠DEF,
因为BE=CF,
所以BC=EF.
因为∠ACB=∠F,
所以△ABC≌△DEF .(ASA )
A
B
D
F
E
C
探究新知
如果“两角及一边”条件中的边是其中一角的对边,情况会怎样呢?你能将它转化为具体的条件吗?
若三角形的两个内角分别是60°和40°,且40°所对的边为2cm,你能画出这个三角形吗
60°
40°
2cm
想一想
60°
40°
这里的条件与“做一做”中的条件有什么相同点与不同点?你能将它转化为“做一做”中的条件吗?
归纳总结
∠A=∠A′(已知),
∠B=∠B′ (已知),
AC=A′C ′(已知),
在△ABC和△A′B′C′中,
所以 △ABC≌△ A′ B′ C′(AAS).
A
B
C
A ′
B ′
C ′
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成 “角角边”或“AAS ” .
书写格式:
典例精析
【例】 在△ABC和△DEF中,∠A=∠D,∠B= ∠E,BC=EF.试说明:AC=DF.
解:
所以△ABC≌△DEF(AAS ).
∠A=∠D,
∠B=∠E.
BC=EF.
在△ABC和△DEF中,
所以AC = DF.
实战演练
如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E.试说明:△BDA≌△AEC .
解:因为BD⊥m,CE⊥m,所以∠ADB=∠CEA=90°,
所以∠ABD+∠BAD=90°.
因为AB⊥AC,
所以∠BAD+∠CAE=90°,
∠ABD=∠CAE.
在△BDA和△AEC中,
∠ADB=∠CEA=90°,
∠ABD=∠CAE,
AB=AC,
所以△BDA≌△AEC(AAS).
课堂练习
1. 在△ABC与△A′B′C′中,已知∠A=44°,∠B=67°∠C′=69° ,∠A′=44°,且AC=A′C′,那么这两个三角形( )
A.一定不全等 B.一定全等 C.不一定全等 D.以上都不对
B
2.如图,已知在△ABD和△ABC中,∠DAB=∠CAB,点A,B,E在同一条直线上,若使△ABD≌△ABC,则还需添加的一个条件是_________________________.(只填一个即可)
∠D=∠C或∠ABD=∠ABC等
课堂练习
3.如图,已知:AD为△ABC的中线,且CF⊥AD于点F,BE⊥AD交AD的延长线于点E.试说明:BE=CF.
解:因为AD为△ABC的中线,
所以BD=CD.因为BE⊥AD,CF⊥AD,
所以∠BED=∠CFD=90°.
在△BED与△CFD中,
所以△BED≌△CFD(AAS).所以BE=CF.
课堂练习
4.如图,点D在AB上,点E在AC上,AB=AC, ∠B=∠C,试说明:AD=AE.
A
B
C
D
E
解:在△ACD和△ABE中,
∠A=∠A(公共角 ),
AC=AB(已知),
∠C=∠B (已知 ),
所以 △ACD≌△ABE(ASA),
所以AD=AE.
课堂练习
5.已知:如图, AB⊥BC,AD⊥DC,∠1=∠2, 试说明:AB=AD.
A
C
D
B
1
2
解: 因为 AB⊥BC,AD⊥DC,
所以 ∠ B=∠D=90 °.
在△ABC和△ADC中,
∠1=∠2 (已知),
∠ B=∠D(已证),
AC=AC (公共边),
所以△ABC≌△ADC(AAS),
所以AB=AD.
总结
角边角和
角角边
内容
有两角及夹边对应相等的两个三角形全等(简写成 “ASA”)
应用
为证明线段和角相等提供了新的证法
注意
注意“角角边”、“角边角”中两角与边的区别
两角分别相等且其中一组等角的对边相等的两个三角形全等,(简写成 “AAS ” )
内容
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
