六年级下册5 数学广角 (鸽巢问题)第1课时《鸽巢问题》示范教学课件(共18张ppt)
文档属性
| 名称 | 六年级下册5 数学广角 (鸽巢问题)第1课时《鸽巢问题》示范教学课件(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-15 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
鸽巢问题
研究 4 支铅笔放入 3 个小盒中的现象
活动要求:
①分组摆一摆,要求将铅笔全部放进去,允许某个小盒空着。
②边摆边记录下来,(记录时:可以画图法表示)看看一共有几种摆法?
二、探究新知
二、探究新知
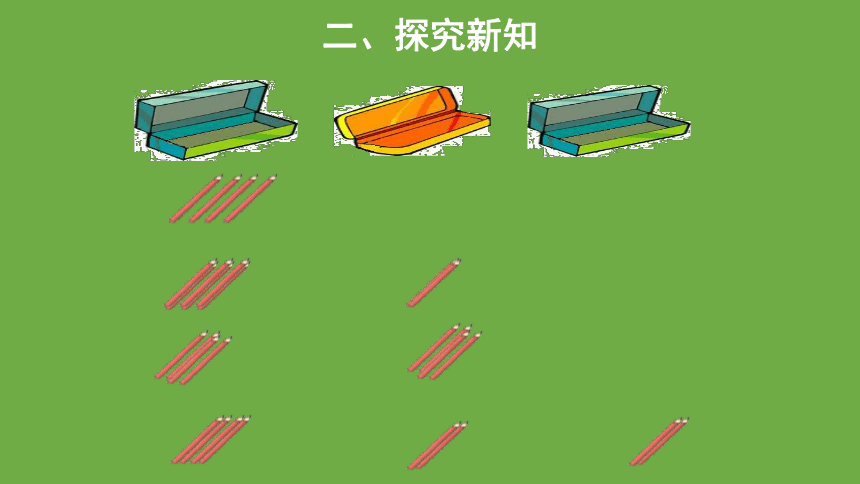
观察四种方法,你有什么发现?
我们发现不管怎么放,总会有一个小盒里面至少有 2 支铅笔。
二、探究新知
二、探究新知
不管怎么放,总会有一个小盒里面至少有 2 支铅笔。
把 4 只鸽子放进 3 个笼子,总有 1 个笼子里至少有 2 只鸽子。
鸽巢问题
抽屉问题
二、探究新知
把 7 本书放进 3 个抽屉,不管怎么放,总有 1 个抽屉里至少有 3 本书。
数的分解法
7
7
7
7
7
7
7
7
7
0
0
0
6
1
5
2
5
0
1
1
0
4
3
4
2
1
3
3
1
3
2
2
二、探究新知
把 7 本书平均分成 3 份, 7 ÷ 3 = 2(本)…… 1(本),若每个抽屉放 2 本,则还剩 1 本。如果把剩下的这 1 本书放进任意 1 个抽屉中,那么这个抽屉里就有 3 本书。
8 ÷ 3 = 2(本)……2(本),剩下 2 本,分别放进其中 2 个抽屉中,使其中 2 个抽屉都变成 3 本,因此把 8 本书放进 3 个抽屉中,不管怎么放,总有 1 个抽屉里至少放进 3 本书。
10 ÷ 3 = 3(本)……1(本),把 10 本书放进 3 个抽屉中,不管怎么放,总有 1 个抽屉里至少放进 4 本书。
假设法
二、探究新知
总结
要把 a 本书放进 3 个抽屉里,如果
a ÷ 3 = b(本)……1(本)或 a ÷ 3 = b(本)……2(本),那么一定有 1 个抽屉里至少放进( b + 1 )本书。
二、探究新知
盒子里有同样大小的红球和篮球各 4 个,要想摸出的球一定有 2 个同色的,至少要摸出几个球?
猜测 1 :只摸 2 个球就能保证这 2 个球同色吗?
结论:只摸 2 个球不能保证这 2 个球同色。
满足条件
满足条件
不满足条件
二、探究新知
猜测 2 :只摸 5 个球就能保证 2 个球同色吗?
结论:只摸 5 个球就能保证 2 个球同色,但是不是最少的。
满足条件
满足条件
满足条件
5 ÷ 2 = 2……1,所以摸出 5 个球时,至少有 3 个球是同色的。
满足条件
二、探究新知
猜测 3 :只摸 3 个球就能保证 2 个球同色吗?
结论:只摸 3 个球就能保证至少 2 个球同色。
满足条件
满足条件
满足条件
3 ÷ 2 = 1……1 ,所以摸出 3 个球时,至少有 2 个球是同色的。
满足条件
二、探究新知
归纳总结
分析题意。
把实际问题转化成“鸽巢问题”,弄清“鸽巢”和分放的“鸽子”。
根据“鸽巢原理”推理并解决问题。
三、巩固练习
1 . 5 只鸽子飞进了 3 个鸽笼,总有一个鸽笼至少飞进了 2 只鸽子。为什么?
5 - 3 = 2(只)
分析:剩下的 2 只鸽子必然要飞进 5 个鸽笼中的一个。
三、巩固练习
2 . 9 个小朋友分 10 块糖,至少有 1 名小朋友分多少块糖?
分析:10 ÷ 9 = 1(块)……1(块),剩下的 1 块糖必然要分给 9 个小朋友中的一个。
答:至少有 1 名小朋友分 2 块糖。
三、巩固练习
3 . 9 个小朋友至少分多少块糖,才能使其中至少有一名小朋友分到4块糖。
3×9=27
27+1=28(块)
答:至少分28 块糖。
三、巩固练习
4 . 把红、黄、蓝、白四种颜色的球各 10 个放到一个袋子里。至少取多少个球,可以保证取到两个颜色相同的球?
我们从最不利的原则去考虑:
假设我们每种颜色的都拿一个,需要拿 4 个,但是没有同色的,要想有同色的需要再拿 1 个球,不论是哪一种颜色的,都一定有 2 个同色的。
4 + 1 = 5 (个)
答:至少取5个球,可以保证取到两个颜色相同的球。
四、课堂小结
运用“鸽巢原理”解决问题的思路和方法:
①分析题意。
②把实际问题转化成“鸽巢问题”,弄清“鸽巢”和分放的“鸽子”。
③根据“鸽巢原理”推理并解决问题。
再见!
鸽巢问题
研究 4 支铅笔放入 3 个小盒中的现象
活动要求:
①分组摆一摆,要求将铅笔全部放进去,允许某个小盒空着。
②边摆边记录下来,(记录时:可以画图法表示)看看一共有几种摆法?
二、探究新知
二、探究新知
观察四种方法,你有什么发现?
我们发现不管怎么放,总会有一个小盒里面至少有 2 支铅笔。
二、探究新知
二、探究新知
不管怎么放,总会有一个小盒里面至少有 2 支铅笔。
把 4 只鸽子放进 3 个笼子,总有 1 个笼子里至少有 2 只鸽子。
鸽巢问题
抽屉问题
二、探究新知
把 7 本书放进 3 个抽屉,不管怎么放,总有 1 个抽屉里至少有 3 本书。
数的分解法
7
7
7
7
7
7
7
7
7
0
0
0
6
1
5
2
5
0
1
1
0
4
3
4
2
1
3
3
1
3
2
2
二、探究新知
把 7 本书平均分成 3 份, 7 ÷ 3 = 2(本)…… 1(本),若每个抽屉放 2 本,则还剩 1 本。如果把剩下的这 1 本书放进任意 1 个抽屉中,那么这个抽屉里就有 3 本书。
8 ÷ 3 = 2(本)……2(本),剩下 2 本,分别放进其中 2 个抽屉中,使其中 2 个抽屉都变成 3 本,因此把 8 本书放进 3 个抽屉中,不管怎么放,总有 1 个抽屉里至少放进 3 本书。
10 ÷ 3 = 3(本)……1(本),把 10 本书放进 3 个抽屉中,不管怎么放,总有 1 个抽屉里至少放进 4 本书。
假设法
二、探究新知
总结
要把 a 本书放进 3 个抽屉里,如果
a ÷ 3 = b(本)……1(本)或 a ÷ 3 = b(本)……2(本),那么一定有 1 个抽屉里至少放进( b + 1 )本书。
二、探究新知
盒子里有同样大小的红球和篮球各 4 个,要想摸出的球一定有 2 个同色的,至少要摸出几个球?
猜测 1 :只摸 2 个球就能保证这 2 个球同色吗?
结论:只摸 2 个球不能保证这 2 个球同色。
满足条件
满足条件
不满足条件
二、探究新知
猜测 2 :只摸 5 个球就能保证 2 个球同色吗?
结论:只摸 5 个球就能保证 2 个球同色,但是不是最少的。
满足条件
满足条件
满足条件
5 ÷ 2 = 2……1,所以摸出 5 个球时,至少有 3 个球是同色的。
满足条件
二、探究新知
猜测 3 :只摸 3 个球就能保证 2 个球同色吗?
结论:只摸 3 个球就能保证至少 2 个球同色。
满足条件
满足条件
满足条件
3 ÷ 2 = 1……1 ,所以摸出 3 个球时,至少有 2 个球是同色的。
满足条件
二、探究新知
归纳总结
分析题意。
把实际问题转化成“鸽巢问题”,弄清“鸽巢”和分放的“鸽子”。
根据“鸽巢原理”推理并解决问题。
三、巩固练习
1 . 5 只鸽子飞进了 3 个鸽笼,总有一个鸽笼至少飞进了 2 只鸽子。为什么?
5 - 3 = 2(只)
分析:剩下的 2 只鸽子必然要飞进 5 个鸽笼中的一个。
三、巩固练习
2 . 9 个小朋友分 10 块糖,至少有 1 名小朋友分多少块糖?
分析:10 ÷ 9 = 1(块)……1(块),剩下的 1 块糖必然要分给 9 个小朋友中的一个。
答:至少有 1 名小朋友分 2 块糖。
三、巩固练习
3 . 9 个小朋友至少分多少块糖,才能使其中至少有一名小朋友分到4块糖。
3×9=27
27+1=28(块)
答:至少分28 块糖。
三、巩固练习
4 . 把红、黄、蓝、白四种颜色的球各 10 个放到一个袋子里。至少取多少个球,可以保证取到两个颜色相同的球?
我们从最不利的原则去考虑:
假设我们每种颜色的都拿一个,需要拿 4 个,但是没有同色的,要想有同色的需要再拿 1 个球,不论是哪一种颜色的,都一定有 2 个同色的。
4 + 1 = 5 (个)
答:至少取5个球,可以保证取到两个颜色相同的球。
四、课堂小结
运用“鸽巢原理”解决问题的思路和方法:
①分析题意。
②把实际问题转化成“鸽巢问题”,弄清“鸽巢”和分放的“鸽子”。
③根据“鸽巢原理”推理并解决问题。
再见!
