2.1 勾股定理的应用(2) 课件[上学期]
文档属性
| 名称 | 2.1 勾股定理的应用(2) 课件[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 656.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-08-09 00:00:00 | ||
图片预览


文档简介
课件18张PPT。勾股定理的应用㈡制作:赵齐猛
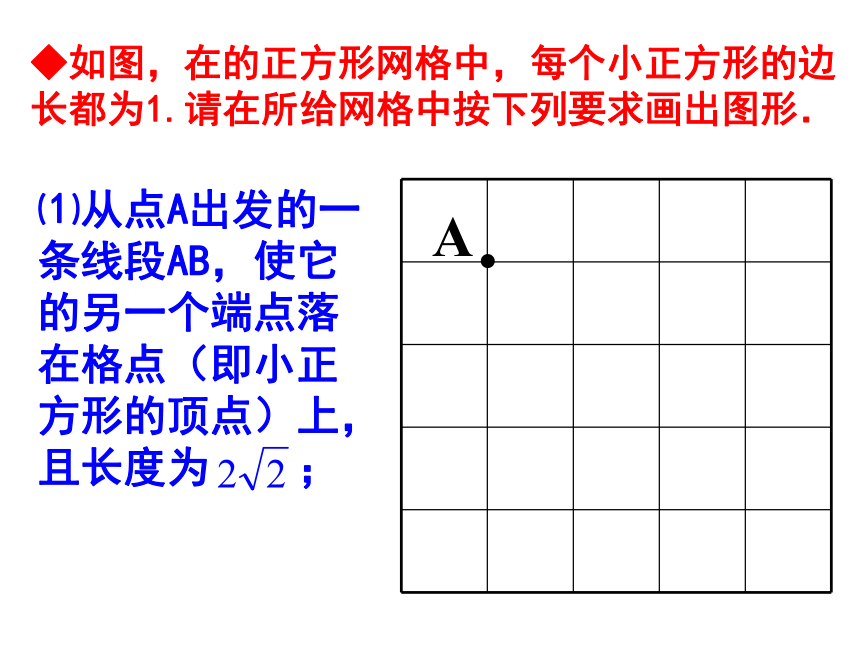
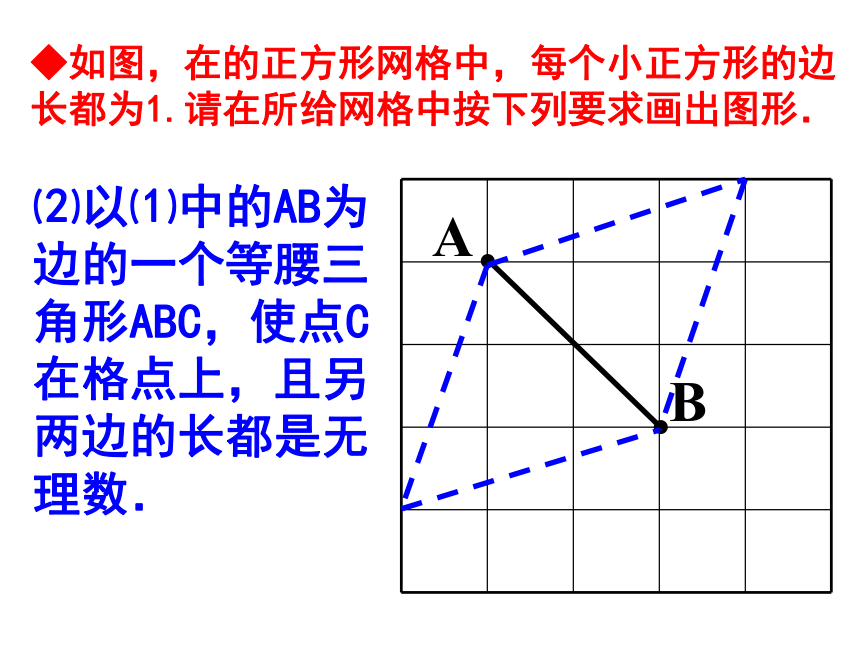
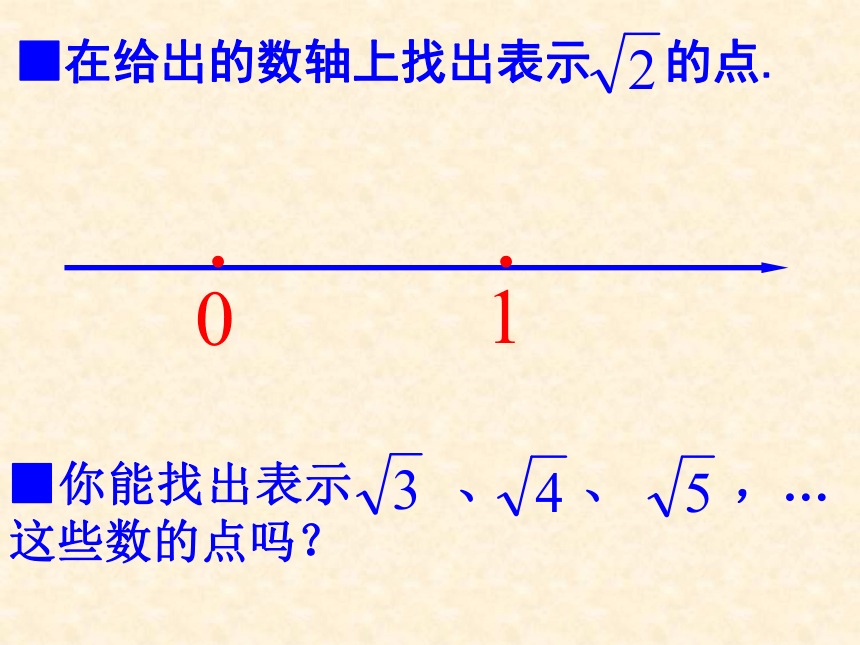
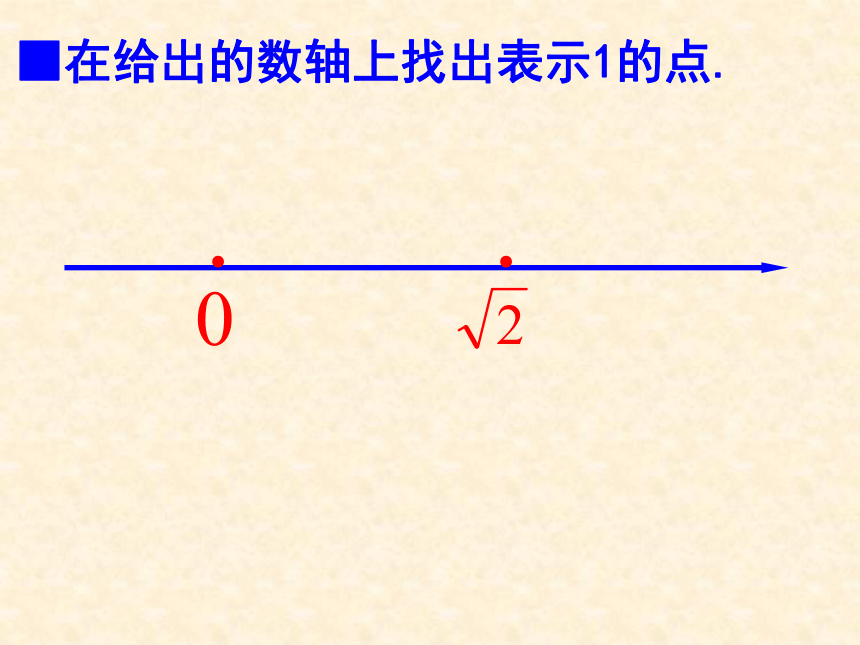
审核:祁海军◆如图,在的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形. ⑴从点A出发的一条线段AB,使它的另一个端点落在格点(即小正方形的顶点)上,且长度为 ; ◆如图,在的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形. ⑵以⑴中的AB为边的一个等腰三角形ABC,使点C在格点上,且另两边的长都是无理数. B.01··■在给出的数轴上找出表示 的点. ■你能找出表示 、 、 ,…这些数的点吗? ■在给出的数轴上找出表示1的点. 0··◆已知等边三角形的边长为a,求它的高和面积. ⑴求它的高.⑵求它的面积. BAC◆在Rt△ABC中,∠ACB=90°,AC=4,BC=3.
求Rt△ABC斜边上的高. ABCD●邮递员从车站O正东1km的邮局A出发,先向正北走了3km到B,又向正西走了4km到C,最后再向正南走了6km到D,那么最终该邮递员与邮局的距离为多少km? ABCDO如图,已知:△ABC中,AD是中线,AE⊥BC于E.
⑴若AB=12,BC=10,AC=8 ,求:DE的长度.如图,已知:△ABC中,AD是中线,AE⊥BC于E.
⑵求证:AB2 - AC2=2BC·DE.如图,已知:等腰直角△ABC中,P为斜边BC上的任一点.
求证:PB2+PC2=2PA2 .D在一个内腔长30cm、宽40 cm、高50 cm的木箱中放一根笔直的细玻璃管,这根玻璃管的长度至多为多少cm? ACBD◆在图中,如果在箱内的A处有一只昆虫,它要在箱壁上爬行到B处,至少要爬多远? CD图①305040CDA.B.CCDA.B.图② 教学反思(1)你认为勾股定理有什么用途?一般如何用?(2)勾股定理与生活实际有什么联系?预习指南勾股定理的应用㈢
审核:祁海军◆如图,在的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形. ⑴从点A出发的一条线段AB,使它的另一个端点落在格点(即小正方形的顶点)上,且长度为 ; ◆如图,在的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形. ⑵以⑴中的AB为边的一个等腰三角形ABC,使点C在格点上,且另两边的长都是无理数. B.01··■在给出的数轴上找出表示 的点. ■你能找出表示 、 、 ,…这些数的点吗? ■在给出的数轴上找出表示1的点. 0··◆已知等边三角形的边长为a,求它的高和面积. ⑴求它的高.⑵求它的面积. BAC◆在Rt△ABC中,∠ACB=90°,AC=4,BC=3.
求Rt△ABC斜边上的高. ABCD●邮递员从车站O正东1km的邮局A出发,先向正北走了3km到B,又向正西走了4km到C,最后再向正南走了6km到D,那么最终该邮递员与邮局的距离为多少km? ABCDO如图,已知:△ABC中,AD是中线,AE⊥BC于E.
⑴若AB=12,BC=10,AC=8 ,求:DE的长度.如图,已知:△ABC中,AD是中线,AE⊥BC于E.
⑵求证:AB2 - AC2=2BC·DE.如图,已知:等腰直角△ABC中,P为斜边BC上的任一点.
求证:PB2+PC2=2PA2 .D在一个内腔长30cm、宽40 cm、高50 cm的木箱中放一根笔直的细玻璃管,这根玻璃管的长度至多为多少cm? ACBD◆在图中,如果在箱内的A处有一只昆虫,它要在箱壁上爬行到B处,至少要爬多远? CD图①305040CDA.B.CCDA.B.图② 教学反思(1)你认为勾股定理有什么用途?一般如何用?(2)勾股定理与生活实际有什么联系?预习指南勾股定理的应用㈢
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
