第2课时《圆柱的表面积》课件(共15张ppt)
文档属性
| 名称 | 第2课时《圆柱的表面积》课件(共15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-15 13:44:02 | ||
图片预览





文档简介
(共15张PPT)
圆柱与圆锥
圆柱的表面积
一、情境导入
制作一个像图中一样大小的新水桶要用多少铁皮?
二、探究新知
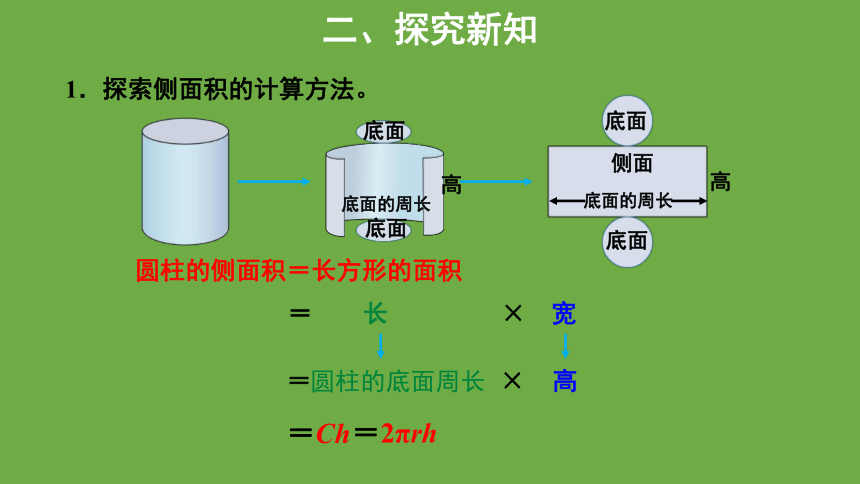
1.探索侧面积的计算方法。
底面
底面
底面的周长
底面
底面
高
底面的周长
侧面
高
圆柱的侧面积=长方形的面积
= 长 × 宽
圆柱的底面周长
高
= ×
=Ch
=2πrh
二、探究新知
2.探索表面积的计算方法。
烟囱
水桶
油漆桶
一个侧面
一个侧面
一个底面
一个侧面
两个底面
二、探究新知
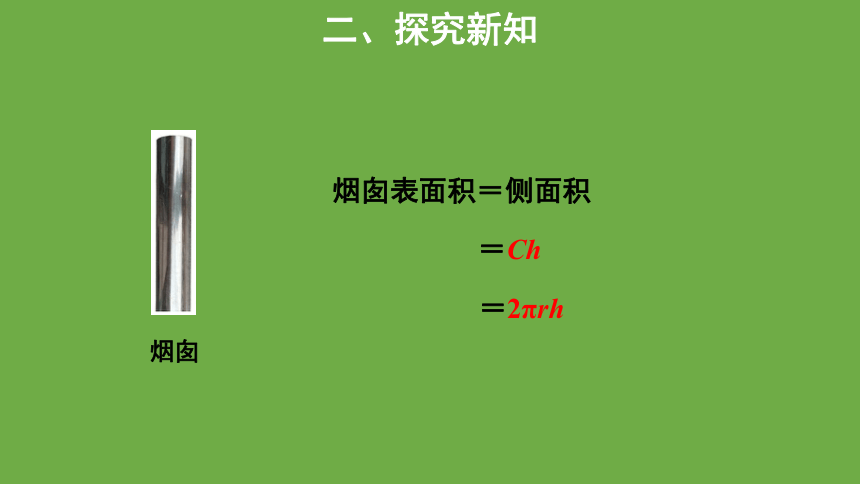
烟囱
烟囱表面积=侧面积
=Ch
=2πrh
二、探究新知
水桶表面积=侧面积+一个底面积
=2πrh+πr2
油漆桶
水桶
油漆桶表面积=侧面积+两个底面积
=2πrh+2πr2
二、探究新知
3.解决问题,能力提升。
一顶圆柱形厨师帽,高30 cm,帽顶直径20 cm,做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数。)
小组讨论:
①求的是厨师帽所用的材料,需要注意些什么?
②“没有底”的帽子如果展开,它由哪几部分组成?
二、探究新知
3.解决问题,能力提升。
①帽子的侧面积:3.14×20×30=1884(cm2)
②帽顶的面积:3.14×(20÷2)2=314(cm2)
③需要用的面料:1884+314=2198≈2200(cm2)
答:做这样一顶帽子至少要用2200 cm2的面料。
为什么最后的结果取2200,而不取2190呢?
一顶圆柱形厨师帽,高30 cm,帽顶直径20 cm,做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数。)
二、探究新知
4.小结。
在实际应用中计算圆柱形物体的表面积,要根据实际情况计算各部分的面积。一般采用进一法取值,以保证原材料够用。
三、巩固练习
1.填空。
(1)一个圆柱侧面展开是一个长为5厘米,宽为3厘米的长方形,圆柱的侧面积是( )平方厘米。
(2)一个圆柱的侧面积是12.56平方厘米,底面周长是6.28厘米,圆柱的高是( )厘米,底面积是( )平方厘米。
(3)一个圆柱的侧面积是6.28平方米,高是10分米,圆柱的底面周长是( )分米。
15
2
3.14
62.8
三、巩固练习
2.用一张长2.5米,宽1.5米的长方形铁皮做一个圆柱形烟筒,这个烟筒的表面积是多少?(接口处忽略不计)
2.5×1.5=3.75(平方米)
答:这个烟筒的表面积是3.75平方米。
三、巩固练习
3.修建一个圆柱形的沼气池,底面直径是3 m,深2 m。在池的侧面与下底面抹上水泥,抹水泥部分的面积是多少平方米?
(结果保留整数)
沼气池的侧面积:3.14×3×2=18.84(m2)
沼气池的底面积:3.14×(3÷2)2=7.065(m2)
抹水泥部分的面积:18.84+7.065=25.905≈26(m2)
答:抹水泥部分的面积是26平方米。
三、巩固练习
4.一顶帽子,上面是圆柱形,用黑布做;帽檐部分是一个圆环,用红布做。做这顶帽子,哪种颜色的布用得多?
黑布的面积:3.14×20×10+3.14×(20÷2)2=942(平方厘米)
红布的面积:3.14×20×20-3.14×10×10=942(平方厘米)
答:两种颜色的布用得一样多。
四、课堂小结
这节课我们学习了圆柱的侧面积、表面积计算公式,知道了如何根据不同的情况求出圆柱的表面积,并能灵活运用求表面积的有关知识解决一些简单的实际问题。
再见
圆柱与圆锥
圆柱的表面积
一、情境导入
制作一个像图中一样大小的新水桶要用多少铁皮?
二、探究新知
1.探索侧面积的计算方法。
底面
底面
底面的周长
底面
底面
高
底面的周长
侧面
高
圆柱的侧面积=长方形的面积
= 长 × 宽
圆柱的底面周长
高
= ×
=Ch
=2πrh
二、探究新知
2.探索表面积的计算方法。
烟囱
水桶
油漆桶
一个侧面
一个侧面
一个底面
一个侧面
两个底面
二、探究新知
烟囱
烟囱表面积=侧面积
=Ch
=2πrh
二、探究新知
水桶表面积=侧面积+一个底面积
=2πrh+πr2
油漆桶
水桶
油漆桶表面积=侧面积+两个底面积
=2πrh+2πr2
二、探究新知
3.解决问题,能力提升。
一顶圆柱形厨师帽,高30 cm,帽顶直径20 cm,做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数。)
小组讨论:
①求的是厨师帽所用的材料,需要注意些什么?
②“没有底”的帽子如果展开,它由哪几部分组成?
二、探究新知
3.解决问题,能力提升。
①帽子的侧面积:3.14×20×30=1884(cm2)
②帽顶的面积:3.14×(20÷2)2=314(cm2)
③需要用的面料:1884+314=2198≈2200(cm2)
答:做这样一顶帽子至少要用2200 cm2的面料。
为什么最后的结果取2200,而不取2190呢?
一顶圆柱形厨师帽,高30 cm,帽顶直径20 cm,做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数。)
二、探究新知
4.小结。
在实际应用中计算圆柱形物体的表面积,要根据实际情况计算各部分的面积。一般采用进一法取值,以保证原材料够用。
三、巩固练习
1.填空。
(1)一个圆柱侧面展开是一个长为5厘米,宽为3厘米的长方形,圆柱的侧面积是( )平方厘米。
(2)一个圆柱的侧面积是12.56平方厘米,底面周长是6.28厘米,圆柱的高是( )厘米,底面积是( )平方厘米。
(3)一个圆柱的侧面积是6.28平方米,高是10分米,圆柱的底面周长是( )分米。
15
2
3.14
62.8
三、巩固练习
2.用一张长2.5米,宽1.5米的长方形铁皮做一个圆柱形烟筒,这个烟筒的表面积是多少?(接口处忽略不计)
2.5×1.5=3.75(平方米)
答:这个烟筒的表面积是3.75平方米。
三、巩固练习
3.修建一个圆柱形的沼气池,底面直径是3 m,深2 m。在池的侧面与下底面抹上水泥,抹水泥部分的面积是多少平方米?
(结果保留整数)
沼气池的侧面积:3.14×3×2=18.84(m2)
沼气池的底面积:3.14×(3÷2)2=7.065(m2)
抹水泥部分的面积:18.84+7.065=25.905≈26(m2)
答:抹水泥部分的面积是26平方米。
三、巩固练习
4.一顶帽子,上面是圆柱形,用黑布做;帽檐部分是一个圆环,用红布做。做这顶帽子,哪种颜色的布用得多?
黑布的面积:3.14×20×10+3.14×(20÷2)2=942(平方厘米)
红布的面积:3.14×20×20-3.14×10×10=942(平方厘米)
答:两种颜色的布用得一样多。
四、课堂小结
这节课我们学习了圆柱的侧面积、表面积计算公式,知道了如何根据不同的情况求出圆柱的表面积,并能灵活运用求表面积的有关知识解决一些简单的实际问题。
再见
