人教版数学八年级下册18.2特殊的平行四边形 巩固训练卷(含答案)
文档属性
| 名称 | 人教版数学八年级下册18.2特殊的平行四边形 巩固训练卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 200.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-16 13:27:26 | ||
图片预览


文档简介
18.2特殊的平行四边形 巩固训练卷
一、单选题
1.如图,菱形ABCD中,对角线AC、BD相交于O,已知BD=6,AC=8,则菱形ABCD的周长为( )
A.40 B.20 C.10 D.5
2.菱形具有而一般矩形不具有的性质是( )
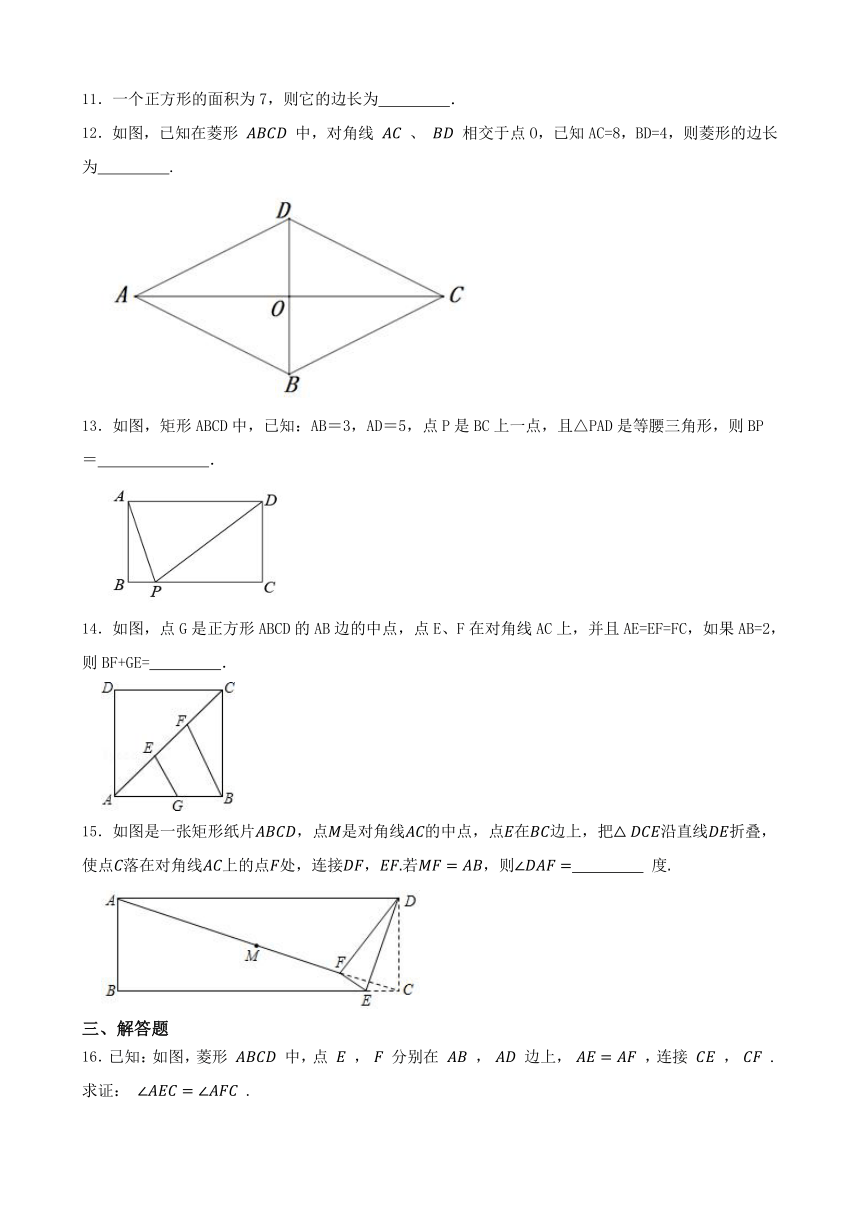
A.对角相等 B.对角线相等
C.对角线互相垂直 D.对角线互相平分
3.张师傅应客户要求加工4个菱形零件.在交付客户之前,需要对4个零件进行检测.根据零件的检测结果,图中有可能不合格的零件是( )
A. B.
C. D.
4.下列说法中错误的是( )
A.对角线垂直的平行四边形是菱形
B.对角线相等的平行四边形是矩形
C.菱形的面积等于对角线乘积的一半
D.对角线互相垂直平分的四边形是正方形
5.要使 ABCD成为矩形,需要添加的条件是( )
A.AB=BC B.AC⊥BD
C.∠ABC=90° D.∠ABD=∠CBD
6.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )cm2
A.4 B.16 C.12 D.8
7.如图,四边形ABCD中,∠B=90°,AB=8,BC=6。点M是对角线AC的中点,点N是AD边的中点,连结BM,MN,若BM=3MN,则线段CD的长是( )
A. B.3 C. D.5
8.如图,在矩形ABCD中,AB=2,AD=4,E为CD的中点,连结AE并延长,交BC的延长线于点F,点P为BC上一点,当∠PAE=∠DAE时,则AP的长度为( )
A. B. C.4 D.
9.矩形具有而一般平行四边形不具有的性质是( )
A.两组对边分别相等 B.两组对角分别相等
C.两条对角线互相平分 D.两条对角线相等
10.如图,在正方形中,点E,F分别在边上,点P是的中点,连接.若,则的度数为( )
A. B. C. D.
二、填空题
11.一个正方形的面积为7,则它的边长为 .
12.如图,已知在菱形 中,对角线 、 相交于点O,已知AC=8,BD=4,则菱形的边长为 .
13.如图,矩形ABCD中,已知:AB=3,AD=5,点P是BC上一点,且△PAD是等腰三角形,则BP= .
14.如图,点G是正方形ABCD的AB边的中点,点E、F在对角线AC上,并且AE=EF=FC,如果AB=2,则BF+GE= .
15.如图是一张矩形纸片,点是对角线的中点,点在边上,把沿直线折叠,使点落在对角线上的点处,连接,若,则 度
三、解答题
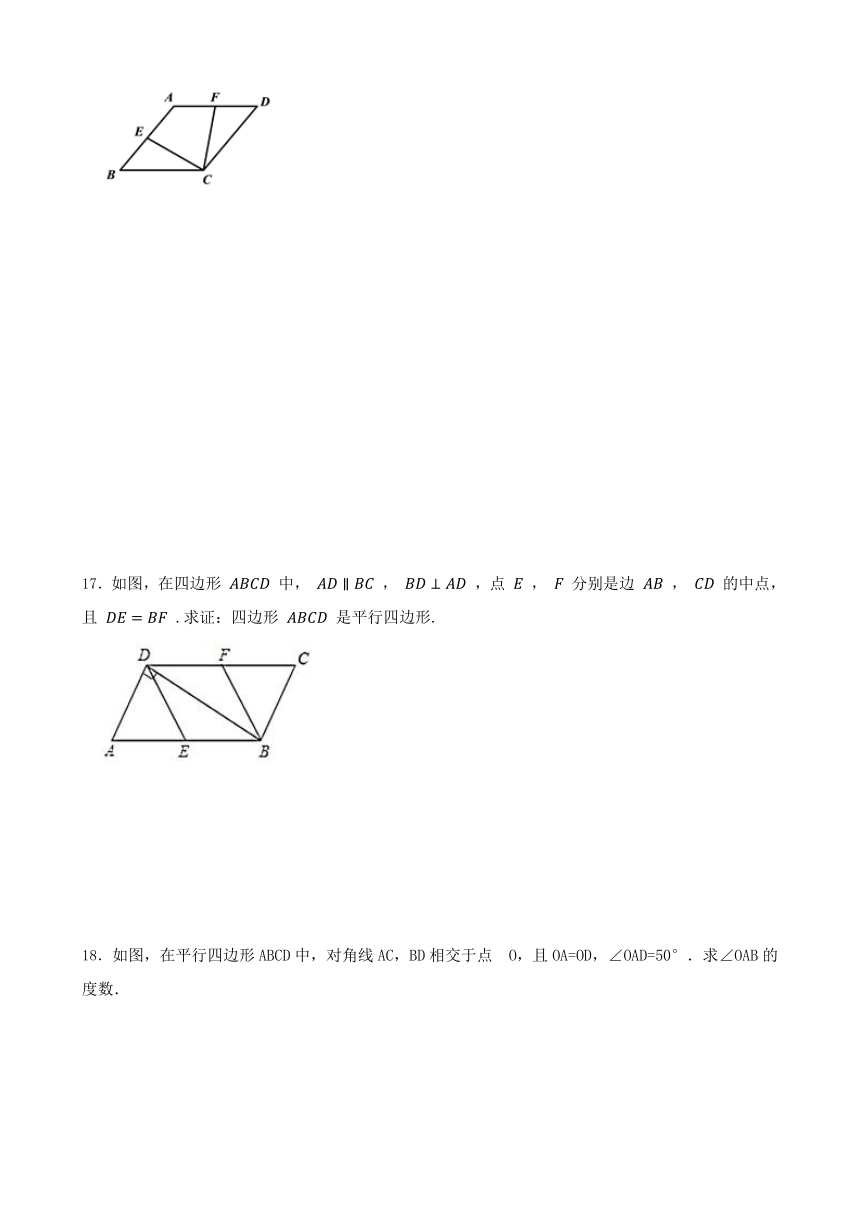
16.已知:如图,菱形 中,点 , 分别在 , 边上, ,连接 , .求证: .
17.如图,在四边形 中, , ,点 , 分别是边 , 的中点,且 .求证:四边形 是平行四边形.
18.如图,在平行四边形ABCD中,对角线AC,BD相交于点 O,且OA=OD,∠OAD=50°.求∠OAB的度数.
19.如图,在菱形ABCD中,对角线AC、BD交于点O, , ,求菱形ABCD的周长.
20.等腰Rt△ABC与等腰Rt△ADE,AB=BC,AD=DE,∠ABC=∠ADE=90°,连接CE,取CE中点G,连接BG,DG,探索BG,DG的关系.
答案解析部分
1.B
2.C
3.C
4.D
5.C
6.D
7.C
8.B
9.D
10.C
11.
12.
13.1,4,2.5
14.
15.18
16.证明:连接 ,如图,
四边形 是菱形,
,
在 和 中, ,
(SAS),
.
17.证明:∵ , ,
∴ ,
∵在 中, 是 的中点,
∴ ,
同理: ,
∵ ,
∴ ,
在 和 中,
∴ ,
∴ .
∴四边形 是平行四边形.
18.解:∵四边形ABCD是平行四边形,
∴OA=,OD=
又∵OA=OD
∴AC=BD
∴四边形ABCD是矩形,
∴∠DAB=90°,
∵∠OAD=50°,
∴∠OAB=∠DAB-∠OAD=40°
19.解:∵四边形ABCD是菱形,
∴ , ,
, .
在 中,由勾股定理,得
,
∴ .
20.解:BG=DG且BG⊥GD,理由如下:
取AC的中点为M,AE的中点为N,连接BM,MG,GN,DN,GD与AE相交于点P.
∵M是AC的中点,G是CD的中点.
∴MG是三角形的中位线.
∴MG∥AE,MG=AE.
∴∠CMG=∠CAE.
∵BM是Rt△ABC斜边AC上的中线,AB=BC.
∴BM=AC.∠BMA=90°.
同理可得GN∥AC,NG=AC,∠DNA=90°,∠ENG=∠CAE,DN=AE.
∴BM=NG,MG=DN,∠CMG=∠ENG.
∴∠AMG=∠ANG.
∴∠BMG=∠DNG.
∴△BMG≌△GND(SAS).
∴BG=DG,∠MGB=∠GDN
∵MG∥AE.
∴∠MGD=∠GPE.
∴∠MGB+∠BGD=∠PND+∠GDN.
∴∠BGD=∠AND=90°,即BG⊥GD.
∴BG=DG且BG⊥GD.
一、单选题
1.如图,菱形ABCD中,对角线AC、BD相交于O,已知BD=6,AC=8,则菱形ABCD的周长为( )
A.40 B.20 C.10 D.5
2.菱形具有而一般矩形不具有的性质是( )
A.对角相等 B.对角线相等
C.对角线互相垂直 D.对角线互相平分
3.张师傅应客户要求加工4个菱形零件.在交付客户之前,需要对4个零件进行检测.根据零件的检测结果,图中有可能不合格的零件是( )
A. B.
C. D.
4.下列说法中错误的是( )
A.对角线垂直的平行四边形是菱形
B.对角线相等的平行四边形是矩形
C.菱形的面积等于对角线乘积的一半
D.对角线互相垂直平分的四边形是正方形
5.要使 ABCD成为矩形,需要添加的条件是( )
A.AB=BC B.AC⊥BD
C.∠ABC=90° D.∠ABD=∠CBD
6.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )cm2
A.4 B.16 C.12 D.8
7.如图,四边形ABCD中,∠B=90°,AB=8,BC=6。点M是对角线AC的中点,点N是AD边的中点,连结BM,MN,若BM=3MN,则线段CD的长是( )
A. B.3 C. D.5
8.如图,在矩形ABCD中,AB=2,AD=4,E为CD的中点,连结AE并延长,交BC的延长线于点F,点P为BC上一点,当∠PAE=∠DAE时,则AP的长度为( )
A. B. C.4 D.
9.矩形具有而一般平行四边形不具有的性质是( )
A.两组对边分别相等 B.两组对角分别相等
C.两条对角线互相平分 D.两条对角线相等
10.如图,在正方形中,点E,F分别在边上,点P是的中点,连接.若,则的度数为( )
A. B. C. D.
二、填空题
11.一个正方形的面积为7,则它的边长为 .
12.如图,已知在菱形 中,对角线 、 相交于点O,已知AC=8,BD=4,则菱形的边长为 .
13.如图,矩形ABCD中,已知:AB=3,AD=5,点P是BC上一点,且△PAD是等腰三角形,则BP= .
14.如图,点G是正方形ABCD的AB边的中点,点E、F在对角线AC上,并且AE=EF=FC,如果AB=2,则BF+GE= .
15.如图是一张矩形纸片,点是对角线的中点,点在边上,把沿直线折叠,使点落在对角线上的点处,连接,若,则 度
三、解答题
16.已知:如图,菱形 中,点 , 分别在 , 边上, ,连接 , .求证: .
17.如图,在四边形 中, , ,点 , 分别是边 , 的中点,且 .求证:四边形 是平行四边形.
18.如图,在平行四边形ABCD中,对角线AC,BD相交于点 O,且OA=OD,∠OAD=50°.求∠OAB的度数.
19.如图,在菱形ABCD中,对角线AC、BD交于点O, , ,求菱形ABCD的周长.
20.等腰Rt△ABC与等腰Rt△ADE,AB=BC,AD=DE,∠ABC=∠ADE=90°,连接CE,取CE中点G,连接BG,DG,探索BG,DG的关系.
答案解析部分
1.B
2.C
3.C
4.D
5.C
6.D
7.C
8.B
9.D
10.C
11.
12.
13.1,4,2.5
14.
15.18
16.证明:连接 ,如图,
四边形 是菱形,
,
在 和 中, ,
(SAS),
.
17.证明:∵ , ,
∴ ,
∵在 中, 是 的中点,
∴ ,
同理: ,
∵ ,
∴ ,
在 和 中,
∴ ,
∴ .
∴四边形 是平行四边形.
18.解:∵四边形ABCD是平行四边形,
∴OA=,OD=
又∵OA=OD
∴AC=BD
∴四边形ABCD是矩形,
∴∠DAB=90°,
∵∠OAD=50°,
∴∠OAB=∠DAB-∠OAD=40°
19.解:∵四边形ABCD是菱形,
∴ , ,
, .
在 中,由勾股定理,得
,
∴ .
20.解:BG=DG且BG⊥GD,理由如下:
取AC的中点为M,AE的中点为N,连接BM,MG,GN,DN,GD与AE相交于点P.
∵M是AC的中点,G是CD的中点.
∴MG是三角形的中位线.
∴MG∥AE,MG=AE.
∴∠CMG=∠CAE.
∵BM是Rt△ABC斜边AC上的中线,AB=BC.
∴BM=AC.∠BMA=90°.
同理可得GN∥AC,NG=AC,∠DNA=90°,∠ENG=∠CAE,DN=AE.
∴BM=NG,MG=DN,∠CMG=∠ENG.
∴∠AMG=∠ANG.
∴∠BMG=∠DNG.
∴△BMG≌△GND(SAS).
∴BG=DG,∠MGB=∠GDN
∵MG∥AE.
∴∠MGD=∠GPE.
∴∠MGB+∠BGD=∠PND+∠GDN.
∴∠BGD=∠AND=90°,即BG⊥GD.
∴BG=DG且BG⊥GD.
