5.1鸽巢问题 (课件)人教版数学六年级下册(共13张PPT)
文档属性
| 名称 | 5.1鸽巢问题 (课件)人教版数学六年级下册(共13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 201.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-15 15:13:53 | ||
图片预览



文档简介
(共13张PPT)
六年级下册数学广角
鸽巢问题
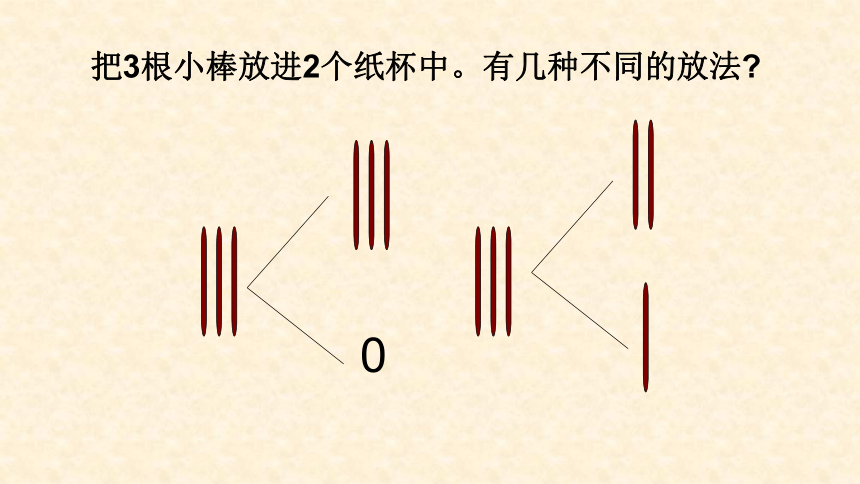
把3根小棒放进2个纸杯中。有几种不同的放法
0
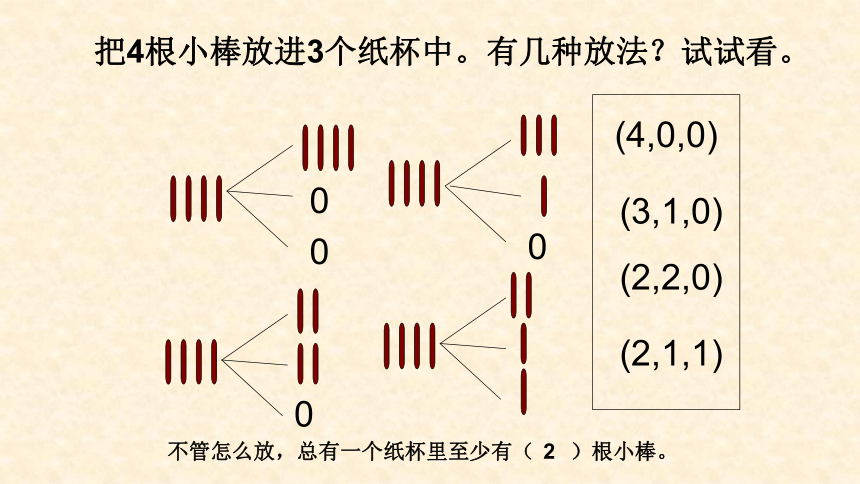
把4根小棒放进3个纸杯中。有几种放法?试试看。
0
0
0
0
(4,0,0)
(3,1,0)
(2,2,0)
(2,1,1)
不管怎么放,总有一个纸杯里至少有( )根小棒。
2
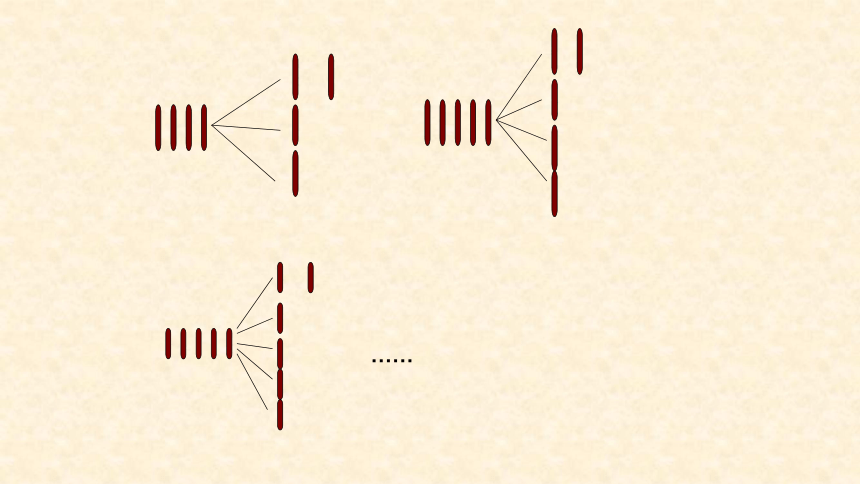
把5根小棒放进4个纸杯中。
猜猜:不管怎么放,总有一个纸杯至少有( )根小棒。
(5,0,0,0)
(4,1,0,0)
(3,2,0,0)
(3,1,1,0)
(2,2,1,0)
(2,1,1,1)
2
把6根小棒放进5个纸杯中。
猜猜:不管怎么放,总有一个纸杯至少有( )根小棒。
把100根小棒放进99个纸杯中。
猜猜:不管怎么放,总有一个纸杯至少有( )根小棒。
……
把10000根小棒放进9999个纸杯中。
猜猜:不管怎么放,总有一个纸杯至少有( )根小棒。
……
……
小棒的数量比纸杯数多1,不管怎么放,总有一个纸杯里至少有2根小棒。
把n+1根小棒放入n个纸杯,不管怎么放,总有一个纸杯里至少有2根小棒。
6只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
6÷5 = 1……1 1+1=2
7只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
7÷5 = 1……2 1+1=2
8只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
9只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
10只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
11只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
11只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
11÷5 = 2……1 2+1=3
12只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
12÷5 = 2……2 2+1=3
18只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
18÷5 = 3……3 3+1=3
解决这类题的方法是:
先用鸽子数除以鸽笼数,再用得到的商加上1。
把5本书进2个抽屉中,不管怎么放,总有一个抽屉至少放进几本书?
把7本书进2个抽屉中,不管怎么放,总有一个抽屉至少放进几本书?
把20本书进个6抽屉中,不管怎么放,总有一个抽屉至少放进几本书?
先用书的本数除以抽屉数,再用得到的商加上1。
先用总环数除以投镖数,再用得到的商加上1。
先用物体数除以抽屉数,再用得到的商加1。
如果把m个物体放入n个抽屉,并且m÷n=a……b(m>n>1),那么不管怎么放,总有一个抽屉至少有( )个物体。
a+1
“抽屉原理”又称“鸽巢原理”,
最先是由19世纪的德国数学家
狄里克雷提出来的,所以又称
“狄里克雷原理”。抽屉原理的应用是千变万化的,用它可以解决许多有趣的问题,并且常常能得到一些令人惊异的结果。
狄利克雷
(1805~1859)
课下思考:
任意写出4个自然数,总有两个数的差是3的倍数。这是为什么?
六年级下册数学广角
鸽巢问题
把3根小棒放进2个纸杯中。有几种不同的放法
0
把4根小棒放进3个纸杯中。有几种放法?试试看。
0
0
0
0
(4,0,0)
(3,1,0)
(2,2,0)
(2,1,1)
不管怎么放,总有一个纸杯里至少有( )根小棒。
2
把5根小棒放进4个纸杯中。
猜猜:不管怎么放,总有一个纸杯至少有( )根小棒。
(5,0,0,0)
(4,1,0,0)
(3,2,0,0)
(3,1,1,0)
(2,2,1,0)
(2,1,1,1)
2
把6根小棒放进5个纸杯中。
猜猜:不管怎么放,总有一个纸杯至少有( )根小棒。
把100根小棒放进99个纸杯中。
猜猜:不管怎么放,总有一个纸杯至少有( )根小棒。
……
把10000根小棒放进9999个纸杯中。
猜猜:不管怎么放,总有一个纸杯至少有( )根小棒。
……
……
小棒的数量比纸杯数多1,不管怎么放,总有一个纸杯里至少有2根小棒。
把n+1根小棒放入n个纸杯,不管怎么放,总有一个纸杯里至少有2根小棒。
6只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
6÷5 = 1……1 1+1=2
7只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
7÷5 = 1……2 1+1=2
8只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
9只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
10只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
11只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
11只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
11÷5 = 2……1 2+1=3
12只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
12÷5 = 2……2 2+1=3
18只鸽子飞回5个鸽笼,至少有几只鸽子飞回同一个鸽笼里,为什么?
18÷5 = 3……3 3+1=3
解决这类题的方法是:
先用鸽子数除以鸽笼数,再用得到的商加上1。
把5本书进2个抽屉中,不管怎么放,总有一个抽屉至少放进几本书?
把7本书进2个抽屉中,不管怎么放,总有一个抽屉至少放进几本书?
把20本书进个6抽屉中,不管怎么放,总有一个抽屉至少放进几本书?
先用书的本数除以抽屉数,再用得到的商加上1。
先用总环数除以投镖数,再用得到的商加上1。
先用物体数除以抽屉数,再用得到的商加1。
如果把m个物体放入n个抽屉,并且m÷n=a……b(m>n>1),那么不管怎么放,总有一个抽屉至少有( )个物体。
a+1
“抽屉原理”又称“鸽巢原理”,
最先是由19世纪的德国数学家
狄里克雷提出来的,所以又称
“狄里克雷原理”。抽屉原理的应用是千变万化的,用它可以解决许多有趣的问题,并且常常能得到一些令人惊异的结果。
狄利克雷
(1805~1859)
课下思考:
任意写出4个自然数,总有两个数的差是3的倍数。这是为什么?
