河南省南阳市2022-2023学年高二下学期期中数学模拟试题(三)(含答案)
文档属性
| 名称 | 河南省南阳市2022-2023学年高二下学期期中数学模拟试题(三)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 742.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-15 00:47:48 | ||
图片预览




文档简介
南阳市2023年春期期中模拟高二年级
数 学 试 题
(考试时间:120分钟 试卷满分:150分)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.为比较相关变量的线性相关程度,5位同学各自研究一组数据,并计算出变量间的相关系数r如表所示:
同学甲 同学乙 同学丙 同学丁 同学戊
相关系数r 0.45 ﹣0.69 0.74 ﹣0.98 0.82
则由表可知( )
A.乙研究的那组数据线性相关程度最低,戊研究的那组数据线性相关程度最高
B.甲研究的那组数据线性相关程度最低,丁研究的那组数据线性相关程度最高
C.乙研究的那组数据线性相关程度最低,丁研究的那组数据线性相关程度最高
D.甲研究的那组数据线性相关程度最低,丙研究的那组数据线性相关程度最高
2.如图所示,水波的半径以1m/s的速度向外扩张,当半径为5m时,这水波面的圆面积的膨胀率是( )m2/s.
A.10π B.15π C.20π D.25π
3.已知数列是等差数列,数列是等比数列,若,,则的值是( )
A. B. C. D.
4.已知函数的导函数为,,则( )
A. B. C. D.
5.已知数列{an}的前n项和Sn=1-5+9-13+17+…+(-1)n-1·(4n-3),则S15+S22-S31的值是 ( )
A.13 B.-76 C.46 D.76
6.设是函数f(x)的导数,若>0,且 x1,x2∈R(x1≠x2),f(x1)+f(x2)<2f(),则下列各项错误的是( )
A.f(2)<f(e)<f(π)
B.<<
C.<f(3)﹣f(2)<
D.<f(3)﹣f(2)<
7.在一项调查中有两个变量x和y,如图是由这两个变量近8年来的取值数据得到的散点图,那么适宜作为y关于x的回归方程的函数类型是( )
A.y=a+bx B.y=p+qcx(q>0)
C.y=m+nx2(n>0) D.
8.已知数列的首项,其前项和为,且满足,则当取得最小值时,( )
A.4 B.5 C.6 D.7
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列运算中正确的是( )
A. B.
C.()′= D.(cos x·sin x)′=-sin 2x+cos2x
10.下列说法正确的是( )
A.在统计学中,独立性检验是检验两个随机事件是否有关系的一种统计方法
B.在两个随机事件的样本数据的列联表中,对角线上数据的乘积相差越大,两个事件有关系的可能性就越小
C.对随机事件X与Y的随机变量的,越小,“X与Y有关系”的可信程度越小
D.两个有线性相关关系的变量x,y的相关系数为r,则越接近于0,x与y之间的线性相关程度越强.
11.已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则称x0是f(x)的一个“青山点”.下列函数中,有“青山点”的是( )
A.f(x)=x2 B.f(x)=e﹣x C.f(x)=Inx D.f(x)=
12.设数列的前n项和为,且,若,则下列结论正确的有( )
A. B.数列单调递增
C.当时,取得最小值 D.时,n的最小值为7
三、填空题:本题共4小题,每小题5分,共20分.
13.已知变量和变量的三对随机观测数据,,,若,,,则成对样本数据的样本相关系数是__________。
14.对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:设f′′(x)是函数f(x)的导数y=f'(x)的导数,若方程f′′(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现视为条件,若函数,则它的对称中心为 ;并计算= .
15.我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为_____日.(结果保留一位小数,参考数据:,)
16.意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一列数:1,1,2,3,5,…,其中从第三项起,每个数等于它前面两个数的和,后来人们把这样的一列数组成的数列称为“斐波那契数列”,记为数列的前项和,则下列结论正确的是__________.
① ② ③ ④
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.设数列{an}满足a1+3a2+…+(2n-1)an=2n.
(1)求{an}的通项公式;
(2)求数列的前n项和.
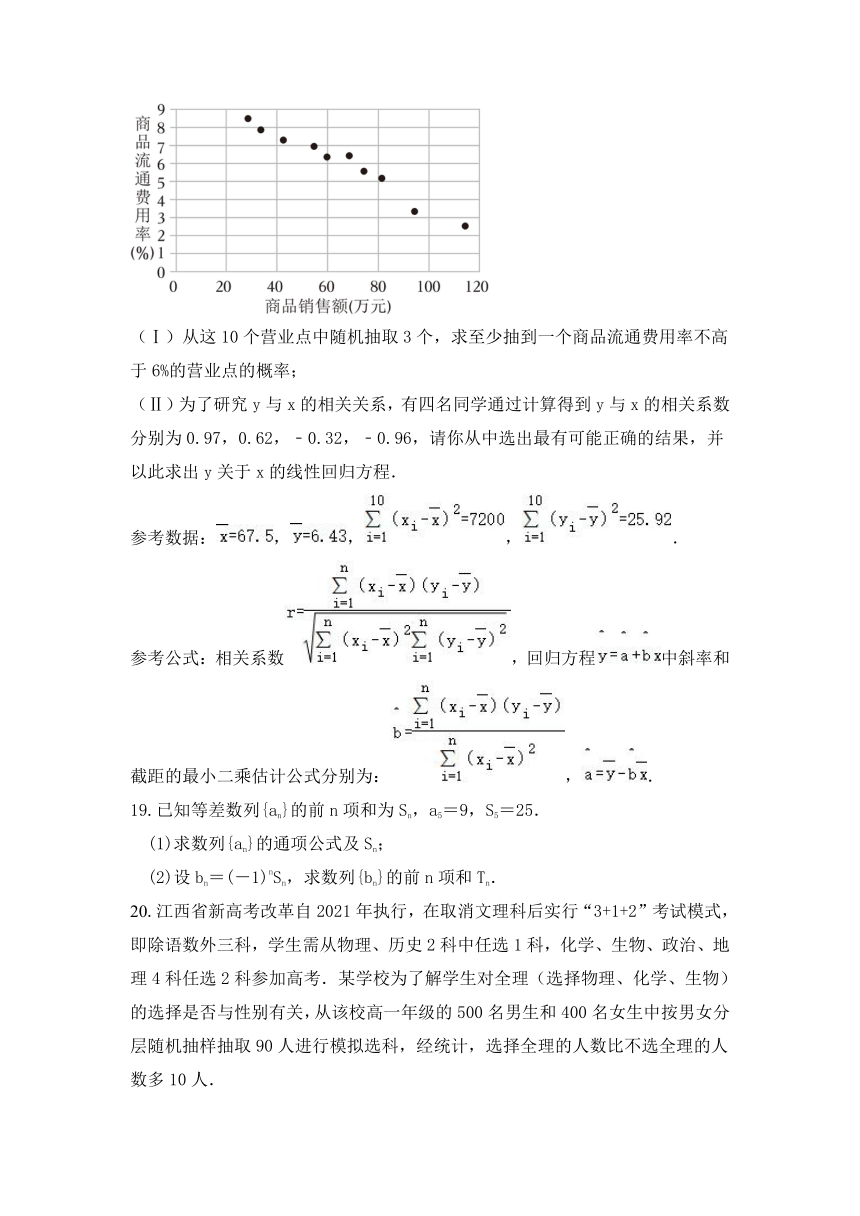
18.商品流通费用率,又称为流通费用水平,是商品流通费用总额(商品在流通过程所耗费劳动与费用总和)对商品销售额的百分比.一定时期内,在实现的销售额一定的情况下,支出的费用越少,表明费用节约程度越高,体现为经济效益就越好.某企业收集了10个营业点的商品销售额x(万元)与商品流通费用率y(%)的有关数据,制作成散点图如图所示:
(Ⅰ)从这10个营业点中随机抽取3个,求至少抽到一个商品流通费用率不高于6%的营业点的概率;
(Ⅱ)为了研究y与x的相关关系,有四名同学通过计算得到y与x的相关系数分别为0.97,0.62,﹣0.32,﹣0.96,请你从中选出最有可能正确的结果,并以此求出y关于x的线性回归方程.
参考数据:,,,.
参考公式:相关系数,回归方程中斜率和截距的最小二乘估计公式分别为:,.
19.已知等差数列{an}的前n项和为Sn,a5=9,S5=25.
(1)求数列{an}的通项公式及Sn;
(2)设bn=(-1)nSn,求数列{bn}的前n项和Tn.
20.江西省新高考改革自2021年执行,在取消文理科后实行“3+1+2”考试模式,即除语数外三科,学生需从物理、历史2科中任选1科,化学、生物、政治、地理4科任选2科参加高考.某学校为了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,从该校高一年级的500名男生和400名女生中按男女分层随机抽样抽取90人进行模拟选科,经统计,选择全理的人数比不选全理的人数多10人.
选择全理 不选择全理 合计
男生 15
女生
合计
(1)完成上面的2×2列联表并判断是否有99.5%的把握认为选择全理与性别有关;
(2)为了解学生选科的理由,随机选取了男生4名,女生2名进行座谈,再从中抽取2名代表作问卷调查,求至少抽到一名女生的概率.
附:,其中n=a+b+c+d.
P(k2≥k) 0.10 0.05 0.025 0.010 0.005 0.001
k 2.706 3.841 5.024 6.635 7.879 10.828
21.已知函数,g(x)=3x +6x+12 和直线m:y=kx+9,且
(1)求a的值;
(2)是否存在k的值,使直线m既是曲线y=f(x)的切线,又是曲线 y=g(x)的切线 如果存在,求出k的值;如果不存在,请说明理由.
22.已知数列{},>0,其前n项和Sn满足Sn=2-2n+1,其中n∈N*.
(1)设=,证明:数列{}是等差数列;
(2)设=·,为数列{}的前n项和,求证:<3;
(3)设=+λ·(λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有>成立。
2023年春期期中模拟高二年级
数 学 试 题 答 案
BABCB,CDB,9,ABD;10,AC;11,ACD;12,ABC.
11.A:f′(x)=2x,由2x=x2可得x=0或x=2,故符合题意;B:f′(x)=﹣e﹣x,由﹣e﹣x=e﹣x可知x不存在,B不符合题意;C:,由=lnx可得xlnx﹣1=0,令g(x)=xlnx﹣1,则g′(x)=lnx+1,
易得当x>时,g′(x)>0,g(x)单调递增,当0<x<时,g′(x)<0,g(x)单调递减,
故当x=时,函数取得极小值,也是最小值g()=﹣<0,当x→+∞时,g(x)→+∞,故一定存在x0,使得g(x0)=0,即存在x0,使得f(x0)=f′(x0),C符合题意;D:,由得x=﹣1,D符合题意.故选:ACD.
0.99;
(,2),4042;
2.6;
②③④;
【分析】对①②,直接求出对应项及求和;对③④,由得, 化简即可;化简即可.
【详解】对①,,,①错;
对②,,故,②对;
对③,由得,
∴,③对
对④,,④对.
故答案为:②③④
18.解:(Ⅰ)由散点图可知,10个营业点中商品流通费用率不高于6%的有4个,
设事件A表示“至少抽到一个商品流通费用率不高于6%的营业点”,
则P(A)=1﹣=1﹣=;
(Ⅱ)由散点图可知,y与x具有线性相关关系,且y随着x的增大而减少,
所以y与x的相关系数为负值,且绝对值接近于1,所以最有可能正确的结果为r=﹣0.96,
所以b==
=r=﹣0.96×=﹣0.96×=﹣0.96×0.06=﹣0.0576,
所以a=﹣b=6.43+0.0576×67.5=10.318,
所以y关于x的线性回归方程为y=﹣0.0576x+10.318.
19.
20.解:(1)从500名男生和400名女生中按男女分层随机抽样抽取90人,男生抽取50人,女生抽取40人,
选择全理的人数比不选全理的人数多10人,所以选择全理的有50人,填写列联表如下:
选择全理 不选择全理 合计
男生 35 15 50
女生 15 25 40
合计 50 40 90
计算K2==9.50625>7.879,
所以有99.5%的把握认为选择全理与性别有关;
(2)记4名男生为a、b、c、d,2名女生为E、F,从中抽取2名,基本事件为:
ab、ac、ad、aE、aF、bc、bd、bE、bF、cd、cE、cF、dE、dF、EF共15种不同取法,
其中至少抽到一名女生的事件为aE、aF、bE、bF、cE、cF、dE、dF、EF共9种不同取法,
故所求的概率为P==.
数 学 试 题
(考试时间:120分钟 试卷满分:150分)
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.为比较相关变量的线性相关程度,5位同学各自研究一组数据,并计算出变量间的相关系数r如表所示:
同学甲 同学乙 同学丙 同学丁 同学戊
相关系数r 0.45 ﹣0.69 0.74 ﹣0.98 0.82
则由表可知( )
A.乙研究的那组数据线性相关程度最低,戊研究的那组数据线性相关程度最高
B.甲研究的那组数据线性相关程度最低,丁研究的那组数据线性相关程度最高
C.乙研究的那组数据线性相关程度最低,丁研究的那组数据线性相关程度最高
D.甲研究的那组数据线性相关程度最低,丙研究的那组数据线性相关程度最高
2.如图所示,水波的半径以1m/s的速度向外扩张,当半径为5m时,这水波面的圆面积的膨胀率是( )m2/s.
A.10π B.15π C.20π D.25π
3.已知数列是等差数列,数列是等比数列,若,,则的值是( )
A. B. C. D.
4.已知函数的导函数为,,则( )
A. B. C. D.
5.已知数列{an}的前n项和Sn=1-5+9-13+17+…+(-1)n-1·(4n-3),则S15+S22-S31的值是 ( )
A.13 B.-76 C.46 D.76
6.设是函数f(x)的导数,若>0,且 x1,x2∈R(x1≠x2),f(x1)+f(x2)<2f(),则下列各项错误的是( )
A.f(2)<f(e)<f(π)
B.<<
C.<f(3)﹣f(2)<
D.<f(3)﹣f(2)<
7.在一项调查中有两个变量x和y,如图是由这两个变量近8年来的取值数据得到的散点图,那么适宜作为y关于x的回归方程的函数类型是( )
A.y=a+bx B.y=p+qcx(q>0)
C.y=m+nx2(n>0) D.
8.已知数列的首项,其前项和为,且满足,则当取得最小值时,( )
A.4 B.5 C.6 D.7
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列运算中正确的是( )
A. B.
C.()′= D.(cos x·sin x)′=-sin 2x+cos2x
10.下列说法正确的是( )
A.在统计学中,独立性检验是检验两个随机事件是否有关系的一种统计方法
B.在两个随机事件的样本数据的列联表中,对角线上数据的乘积相差越大,两个事件有关系的可能性就越小
C.对随机事件X与Y的随机变量的,越小,“X与Y有关系”的可信程度越小
D.两个有线性相关关系的变量x,y的相关系数为r,则越接近于0,x与y之间的线性相关程度越强.
11.已知函数f(x)及其导数f′(x),若存在x0,使得f(x0)=f′(x0),则称x0是f(x)的一个“青山点”.下列函数中,有“青山点”的是( )
A.f(x)=x2 B.f(x)=e﹣x C.f(x)=Inx D.f(x)=
12.设数列的前n项和为,且,若,则下列结论正确的有( )
A. B.数列单调递增
C.当时,取得最小值 D.时,n的最小值为7
三、填空题:本题共4小题,每小题5分,共20分.
13.已知变量和变量的三对随机观测数据,,,若,,,则成对样本数据的样本相关系数是__________。
14.对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:设f′′(x)是函数f(x)的导数y=f'(x)的导数,若方程f′′(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现视为条件,若函数,则它的对称中心为 ;并计算= .
15.我国古代数学著作《九章算术》有如下问题:“今有蒲(水生植物名)生一日,长三尺;莞(植物名,俗称水葱、席子草)生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”意思是:今有蒲生长1日,长为3尺;莞生长1日,长为1尺.蒲的生长逐日减半,莞的生长逐日增加1倍.若蒲、莞长度相等,则所需的时间约为_____日.(结果保留一位小数,参考数据:,)
16.意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一列数:1,1,2,3,5,…,其中从第三项起,每个数等于它前面两个数的和,后来人们把这样的一列数组成的数列称为“斐波那契数列”,记为数列的前项和,则下列结论正确的是__________.
① ② ③ ④
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.设数列{an}满足a1+3a2+…+(2n-1)an=2n.
(1)求{an}的通项公式;
(2)求数列的前n项和.
18.商品流通费用率,又称为流通费用水平,是商品流通费用总额(商品在流通过程所耗费劳动与费用总和)对商品销售额的百分比.一定时期内,在实现的销售额一定的情况下,支出的费用越少,表明费用节约程度越高,体现为经济效益就越好.某企业收集了10个营业点的商品销售额x(万元)与商品流通费用率y(%)的有关数据,制作成散点图如图所示:
(Ⅰ)从这10个营业点中随机抽取3个,求至少抽到一个商品流通费用率不高于6%的营业点的概率;
(Ⅱ)为了研究y与x的相关关系,有四名同学通过计算得到y与x的相关系数分别为0.97,0.62,﹣0.32,﹣0.96,请你从中选出最有可能正确的结果,并以此求出y关于x的线性回归方程.
参考数据:,,,.
参考公式:相关系数,回归方程中斜率和截距的最小二乘估计公式分别为:,.
19.已知等差数列{an}的前n项和为Sn,a5=9,S5=25.
(1)求数列{an}的通项公式及Sn;
(2)设bn=(-1)nSn,求数列{bn}的前n项和Tn.
20.江西省新高考改革自2021年执行,在取消文理科后实行“3+1+2”考试模式,即除语数外三科,学生需从物理、历史2科中任选1科,化学、生物、政治、地理4科任选2科参加高考.某学校为了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,从该校高一年级的500名男生和400名女生中按男女分层随机抽样抽取90人进行模拟选科,经统计,选择全理的人数比不选全理的人数多10人.
选择全理 不选择全理 合计
男生 15
女生
合计
(1)完成上面的2×2列联表并判断是否有99.5%的把握认为选择全理与性别有关;
(2)为了解学生选科的理由,随机选取了男生4名,女生2名进行座谈,再从中抽取2名代表作问卷调查,求至少抽到一名女生的概率.
附:,其中n=a+b+c+d.
P(k2≥k) 0.10 0.05 0.025 0.010 0.005 0.001
k 2.706 3.841 5.024 6.635 7.879 10.828
21.已知函数,g(x)=3x +6x+12 和直线m:y=kx+9,且
(1)求a的值;
(2)是否存在k的值,使直线m既是曲线y=f(x)的切线,又是曲线 y=g(x)的切线 如果存在,求出k的值;如果不存在,请说明理由.
22.已知数列{},>0,其前n项和Sn满足Sn=2-2n+1,其中n∈N*.
(1)设=,证明:数列{}是等差数列;
(2)设=·,为数列{}的前n项和,求证:<3;
(3)设=+λ·(λ为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有>成立。
2023年春期期中模拟高二年级
数 学 试 题 答 案
BABCB,CDB,9,ABD;10,AC;11,ACD;12,ABC.
11.A:f′(x)=2x,由2x=x2可得x=0或x=2,故符合题意;B:f′(x)=﹣e﹣x,由﹣e﹣x=e﹣x可知x不存在,B不符合题意;C:,由=lnx可得xlnx﹣1=0,令g(x)=xlnx﹣1,则g′(x)=lnx+1,
易得当x>时,g′(x)>0,g(x)单调递增,当0<x<时,g′(x)<0,g(x)单调递减,
故当x=时,函数取得极小值,也是最小值g()=﹣<0,当x→+∞时,g(x)→+∞,故一定存在x0,使得g(x0)=0,即存在x0,使得f(x0)=f′(x0),C符合题意;D:,由得x=﹣1,D符合题意.故选:ACD.
0.99;
(,2),4042;
2.6;
②③④;
【分析】对①②,直接求出对应项及求和;对③④,由得, 化简即可;化简即可.
【详解】对①,,,①错;
对②,,故,②对;
对③,由得,
∴,③对
对④,,④对.
故答案为:②③④
18.解:(Ⅰ)由散点图可知,10个营业点中商品流通费用率不高于6%的有4个,
设事件A表示“至少抽到一个商品流通费用率不高于6%的营业点”,
则P(A)=1﹣=1﹣=;
(Ⅱ)由散点图可知,y与x具有线性相关关系,且y随着x的增大而减少,
所以y与x的相关系数为负值,且绝对值接近于1,所以最有可能正确的结果为r=﹣0.96,
所以b==
=r=﹣0.96×=﹣0.96×=﹣0.96×0.06=﹣0.0576,
所以a=﹣b=6.43+0.0576×67.5=10.318,
所以y关于x的线性回归方程为y=﹣0.0576x+10.318.
19.
20.解:(1)从500名男生和400名女生中按男女分层随机抽样抽取90人,男生抽取50人,女生抽取40人,
选择全理的人数比不选全理的人数多10人,所以选择全理的有50人,填写列联表如下:
选择全理 不选择全理 合计
男生 35 15 50
女生 15 25 40
合计 50 40 90
计算K2==9.50625>7.879,
所以有99.5%的把握认为选择全理与性别有关;
(2)记4名男生为a、b、c、d,2名女生为E、F,从中抽取2名,基本事件为:
ab、ac、ad、aE、aF、bc、bd、bE、bF、cd、cE、cF、dE、dF、EF共15种不同取法,
其中至少抽到一名女生的事件为aE、aF、bE、bF、cE、cF、dE、dF、EF共9种不同取法,
故所求的概率为P==.
同课章节目录
