北师大版八年级数学上册第1章勾股定理单元测试 (含解析)
文档属性
| 名称 | 北师大版八年级数学上册第1章勾股定理单元测试 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 394.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 00:00:00 | ||
图片预览


文档简介
北师大版八上勾股定理单元测试
(共23题,共100分)
一、选择题(共10题,共30分)
(3分)如图,矩形 中,,,点 , 在数轴上,若以点 为圆心,对角线 的长为半径作弧交数轴的正半轴于点 ,则点 表示的数为
A. B. C. D.
(3分)在 中,,,,则 的值是
A. B. C. D.
(3分)已知 , 是线段 上的两点,,,以点 为圆心, 长为半径画弧;再以点 为圆心, 长为半径画弧、两弧交于点 ,连接 ,,则 一定是
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
(3分)三角形的三边长分别为 ,,,且满足等式:,则此三角形是
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
(3分)一架 分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端 分米.如果梯子的顶端沿墙下滑 分米,那么梯足将滑动
A. 分米 B. 分米 C. 分米 D. 分米
(3分)下列各组数中,能构成直角三角形的是
A.,, B.,, C.,, D.,,
(3分)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为 ,较短直角边长为 ,若 ,大正方形的面积为 ,则小正方形的面积为
A. B. C. D.
(3分)如图,在长方形纸片 中,,,现将其沿 对折,使得点 与点 重合,则 的长为
A. B. C. D.
(3分)如图,在 中,,,,点 在 上,, 交 于点 ,交 于点 ,则 的长是
A. B. C. D.
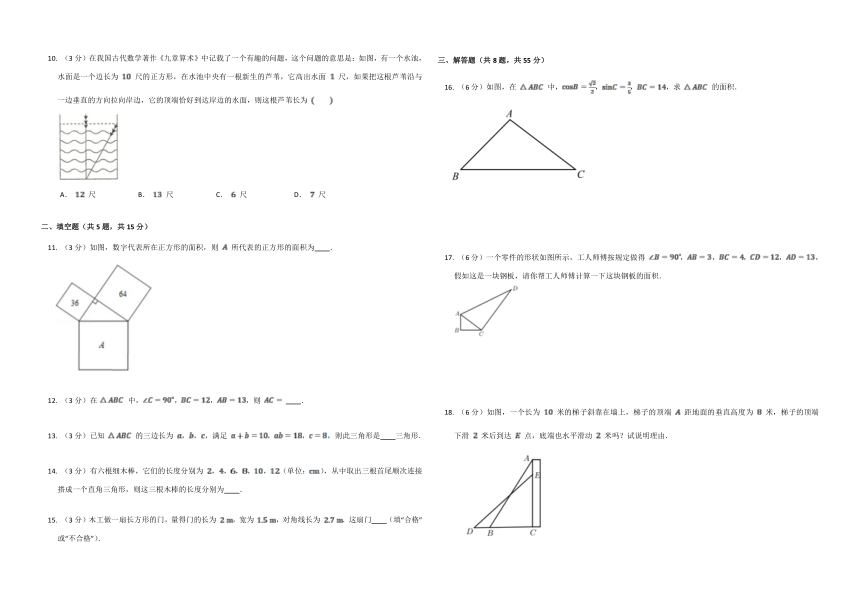
(3分)在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:如图,有一个水池,水面是一个边长为 尺的正方形,在水池中央有一根新生的芦苇,它高出水面 尺,如果把这根芦苇沿与一边垂直的方向拉向岸边,它的顶端恰好到达岸边的水面,则这根芦苇长为
A. 尺 B. 尺 C. 尺 D. 尺
二、填空题(共5题,共15分)
(3分)如图,数字代表所在正方形的面积,则 所代表的正方形的面积为 .
(3分)在 中,,,,则 .
(3分)已知 的三边长为 ,,,满足 ,,,则此三角形是 三角形.
(3分)有六根细木棒,它们的长度分别为 ,,,,,(单位:),从中取出三根首尾顺次连接搭成一个直角三角形,则这三根木棒的长度分别为 .
(3分)木工做一扇长方形的门,量得门的长为 ,宽为 ,对角线长为 .这扇门 (填“合格”或“不合格”).
三、解答题(共8题,共55分)
(6分)如图,在 中,,,,求 的面积.
(6分)一个零件的形状如图所示,工人师傅按规定做得 ,,,,,假如这是一块钢板,请你帮工人师傅计算一下这块钢板的面积.
(6分)如图,一个长为 米的梯子斜靠在墙上,梯子的顶端 距地面的垂直高度为 米,梯子的顶端下滑 米后到达 点,底端也水平滑动 米吗?试说明理由.
(6分)在甲村至乙村的公路旁有一块山地正在开发,现有一 处需要爆破,已知点 与公路上的停靠站 的距离为 米,与公路上另一停靠站 的距离为 米,且 ,如图,为了安全起见,爆破点 周围半径 米范围内不得进入,问在进行爆破时,公路 段是否有危险,是否而需要暂时封锁?请通过计算进行说明.
(6分)如图,已知 ,,,.求证: 是 的中点.
(8分)如图所示,折叠长方形一边 ,点 落在 边的点 处,已知 厘米, 厘米,求 的长.
(8分)如图,四边形 中,,,,,.
(1) 判断 是否是直角,并说明理由.
(2) 求四边形 的面积.
(9分)如图,在等腰直角 中,, 是线段 上一点(),连接 ,过点 作 的垂线,交 的延长线于点 ,交 的延长线于点 .
(1) 依题意补全图形.
(2) 若 ,求 的大小(用含 的式子表示)
(3) 若点 在线段 上,,连接 .
①判断 与 的位置关系并证明.
②用等式表示 ,, 之间的数量关系为 .
答案
一、选择题(共10题,共30分)
1. 【答案】A
【知识点】勾股定理
2. 【答案】B
【知识点】正弦、勾股定理
3. 【答案】B
【知识点】勾股逆定理
4. 【答案】B
【知识点】勾股逆定理
5. 【答案】D
【知识点】勾股定理的实际应用
6. 【答案】B
【知识点】勾股逆定理
7. 【答案】C
【解析】如图所示:
,
,
大正方形的面积为 ,
,
小正方形的面积为 .
【知识点】勾股定理
8. 【答案】B
【知识点】勾股定理之折叠问题
9. 【答案】A
【解析】连接 ,如图所示:
在 中,,,,
,
,,
,,
,
在 和 中,
,
,
,
设 ,则 ,
在 中,由勾股定理得:,
即 ,
解得:;
.
【知识点】勾股定理
10. 【答案】B
【知识点】勾股定理的实际应用
二、填空题(共5题,共15分)
11. 【答案】
【解析】由题意可知,直角三角形中,一条直角边的平方 ,一直角边的平方 ,则斜边的平方 .
【知识点】勾股定理
12. 【答案】
【知识点】勾股定理
13. 【答案】直角
【解析】 ,,,
,
又 ,
,
此三角形是直角三角形.
【知识点】勾股逆定理
14. 【答案】 ,,
【知识点】勾股逆定理
15. 【答案】不合格
【知识点】勾股定理的实际应用
三、解答题(共8题,共55分)
16. 【答案】 .
【知识点】余弦、勾股定理、正弦
17. 【答案】在 中,,
,
在 中,,
,
【知识点】勾股逆定理
18. 【答案】由题意可知,,,,
在 中,由勾股定理得:
,
当 滑到 时,,
;
在 中,
,
.
答:梯子的顶端下滑 米后,底端将水平滑动 米.
【知识点】勾股定理、勾股定理的实际应用
19. 【答案】如图,过 作 于 ,
米, 米,,
根据勾股定理得 米,
,
米.
米 米,故有危险,
因此 段公路需要暂时封锁.
【知识点】勾股定理的实际应用
20. 【答案】提示:连接 ,,证 .
【知识点】勾股定理
21. 【答案】折叠长方形一边 ,
点 落在 边的点 处,
所以 厘米,
在 中,
厘米, 厘米,
由勾股定理,得:
,
,
(厘米),
(厘米).
【知识点】勾股定理之折叠问题
22. 【答案】
(1) 连接 .
,
,
,
,
是直角三角形,即 是直角.
(2) ,
【知识点】勾股逆定理、三角形的面积、勾股定理
23. 【答案】
(1) 补全图形,如图.
(2) ,,
,
,
,
交 的延长线于点 ,
,
,
.
(3) ①连接 交 于点 ,延长 交 于点 ,如图,
,,,
,
,
,
,,
,
,
,
,
.
②
【知识点】边角边、等腰直角三角形的判定、等腰直角三角形的性质、垂线、勾股定理
(共23题,共100分)
一、选择题(共10题,共30分)
(3分)如图,矩形 中,,,点 , 在数轴上,若以点 为圆心,对角线 的长为半径作弧交数轴的正半轴于点 ,则点 表示的数为
A. B. C. D.
(3分)在 中,,,,则 的值是
A. B. C. D.
(3分)已知 , 是线段 上的两点,,,以点 为圆心, 长为半径画弧;再以点 为圆心, 长为半径画弧、两弧交于点 ,连接 ,,则 一定是
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
(3分)三角形的三边长分别为 ,,,且满足等式:,则此三角形是
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
(3分)一架 分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端 分米.如果梯子的顶端沿墙下滑 分米,那么梯足将滑动
A. 分米 B. 分米 C. 分米 D. 分米
(3分)下列各组数中,能构成直角三角形的是
A.,, B.,, C.,, D.,,
(3分)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为 ,较短直角边长为 ,若 ,大正方形的面积为 ,则小正方形的面积为
A. B. C. D.
(3分)如图,在长方形纸片 中,,,现将其沿 对折,使得点 与点 重合,则 的长为
A. B. C. D.
(3分)如图,在 中,,,,点 在 上,, 交 于点 ,交 于点 ,则 的长是
A. B. C. D.
(3分)在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:如图,有一个水池,水面是一个边长为 尺的正方形,在水池中央有一根新生的芦苇,它高出水面 尺,如果把这根芦苇沿与一边垂直的方向拉向岸边,它的顶端恰好到达岸边的水面,则这根芦苇长为
A. 尺 B. 尺 C. 尺 D. 尺
二、填空题(共5题,共15分)
(3分)如图,数字代表所在正方形的面积,则 所代表的正方形的面积为 .
(3分)在 中,,,,则 .
(3分)已知 的三边长为 ,,,满足 ,,,则此三角形是 三角形.
(3分)有六根细木棒,它们的长度分别为 ,,,,,(单位:),从中取出三根首尾顺次连接搭成一个直角三角形,则这三根木棒的长度分别为 .
(3分)木工做一扇长方形的门,量得门的长为 ,宽为 ,对角线长为 .这扇门 (填“合格”或“不合格”).
三、解答题(共8题,共55分)
(6分)如图,在 中,,,,求 的面积.
(6分)一个零件的形状如图所示,工人师傅按规定做得 ,,,,,假如这是一块钢板,请你帮工人师傅计算一下这块钢板的面积.
(6分)如图,一个长为 米的梯子斜靠在墙上,梯子的顶端 距地面的垂直高度为 米,梯子的顶端下滑 米后到达 点,底端也水平滑动 米吗?试说明理由.
(6分)在甲村至乙村的公路旁有一块山地正在开发,现有一 处需要爆破,已知点 与公路上的停靠站 的距离为 米,与公路上另一停靠站 的距离为 米,且 ,如图,为了安全起见,爆破点 周围半径 米范围内不得进入,问在进行爆破时,公路 段是否有危险,是否而需要暂时封锁?请通过计算进行说明.
(6分)如图,已知 ,,,.求证: 是 的中点.
(8分)如图所示,折叠长方形一边 ,点 落在 边的点 处,已知 厘米, 厘米,求 的长.
(8分)如图,四边形 中,,,,,.
(1) 判断 是否是直角,并说明理由.
(2) 求四边形 的面积.
(9分)如图,在等腰直角 中,, 是线段 上一点(),连接 ,过点 作 的垂线,交 的延长线于点 ,交 的延长线于点 .
(1) 依题意补全图形.
(2) 若 ,求 的大小(用含 的式子表示)
(3) 若点 在线段 上,,连接 .
①判断 与 的位置关系并证明.
②用等式表示 ,, 之间的数量关系为 .
答案
一、选择题(共10题,共30分)
1. 【答案】A
【知识点】勾股定理
2. 【答案】B
【知识点】正弦、勾股定理
3. 【答案】B
【知识点】勾股逆定理
4. 【答案】B
【知识点】勾股逆定理
5. 【答案】D
【知识点】勾股定理的实际应用
6. 【答案】B
【知识点】勾股逆定理
7. 【答案】C
【解析】如图所示:
,
,
大正方形的面积为 ,
,
小正方形的面积为 .
【知识点】勾股定理
8. 【答案】B
【知识点】勾股定理之折叠问题
9. 【答案】A
【解析】连接 ,如图所示:
在 中,,,,
,
,,
,,
,
在 和 中,
,
,
,
设 ,则 ,
在 中,由勾股定理得:,
即 ,
解得:;
.
【知识点】勾股定理
10. 【答案】B
【知识点】勾股定理的实际应用
二、填空题(共5题,共15分)
11. 【答案】
【解析】由题意可知,直角三角形中,一条直角边的平方 ,一直角边的平方 ,则斜边的平方 .
【知识点】勾股定理
12. 【答案】
【知识点】勾股定理
13. 【答案】直角
【解析】 ,,,
,
又 ,
,
此三角形是直角三角形.
【知识点】勾股逆定理
14. 【答案】 ,,
【知识点】勾股逆定理
15. 【答案】不合格
【知识点】勾股定理的实际应用
三、解答题(共8题,共55分)
16. 【答案】 .
【知识点】余弦、勾股定理、正弦
17. 【答案】在 中,,
,
在 中,,
,
【知识点】勾股逆定理
18. 【答案】由题意可知,,,,
在 中,由勾股定理得:
,
当 滑到 时,,
;
在 中,
,
.
答:梯子的顶端下滑 米后,底端将水平滑动 米.
【知识点】勾股定理、勾股定理的实际应用
19. 【答案】如图,过 作 于 ,
米, 米,,
根据勾股定理得 米,
,
米.
米 米,故有危险,
因此 段公路需要暂时封锁.
【知识点】勾股定理的实际应用
20. 【答案】提示:连接 ,,证 .
【知识点】勾股定理
21. 【答案】折叠长方形一边 ,
点 落在 边的点 处,
所以 厘米,
在 中,
厘米, 厘米,
由勾股定理,得:
,
,
(厘米),
(厘米).
【知识点】勾股定理之折叠问题
22. 【答案】
(1) 连接 .
,
,
,
,
是直角三角形,即 是直角.
(2) ,
【知识点】勾股逆定理、三角形的面积、勾股定理
23. 【答案】
(1) 补全图形,如图.
(2) ,,
,
,
,
交 的延长线于点 ,
,
,
.
(3) ①连接 交 于点 ,延长 交 于点 ,如图,
,,,
,
,
,
,,
,
,
,
,
.
②
【知识点】边角边、等腰直角三角形的判定、等腰直角三角形的性质、垂线、勾股定理
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
