第4章直线和角单元测试 含答案 沪科版七年级数学上册
文档属性
| 名称 | 第4章直线和角单元测试 含答案 沪科版七年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1019.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 14:57:14 | ||
图片预览



文档简介
沪科版七上直线和角单元测试
(共26题,共120分)
一、选择题(共10题,共30分)
(3分)用一个平面去截一个正方体,截面可能是
A.七边形 B.圆 C.长方形 D.圆锥
(3分)如图,小军同学用小刀沿虚线将一半圆形纸片剪掉右上角,发现剩下图形的周长比原半圆形的周长要小,能正确解释这一现象的数学知识是
A.经过两点有且只有一条直线 B.经过一点有无数条直线
C.两点之间,线段最短 D.部分小于总体
(3分)已知点 ,, 在同一条直线上,若线段 ,,,则下列判断正确的是
A.点 在线段 上 B.点 在线段 上
C.点 在线段 上 D.点 在线段 的延长线上
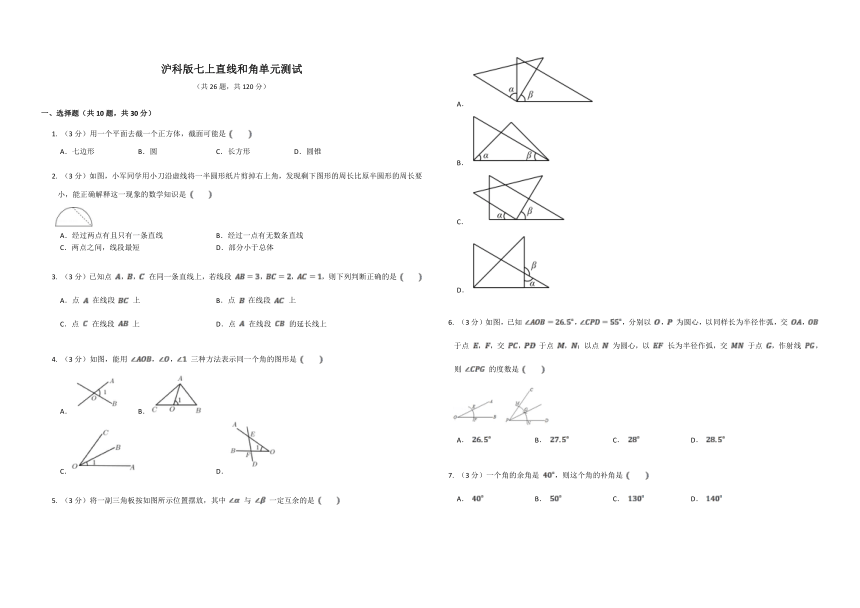
(3分)如图,能用 ,, 三种方法表示同一个角的图形是
A. B.
C. D.
(3分)将一副三角板按如图所示位置摆放,其中 与 一定互余的是
A.
B.
C.
D.
(3分)如图,已知 ,,分别以 , 为圆心,以同样长为半径作弧,交 , 于点 ,,交 , 于点 ,;以点 为圆心,以 长为半径作弧,交 于点 ,作射线 ,则 的度数是
A. B. C. D.
(3分)一个角的余角是 ,则这个角的补角是
A. B. C. D.
(3分)如图,若点 在点 北偏西 的方向上,点 在点 的南偏东 的方向上,则 (小于平角)的度数等于
A. B. C. D.
(3分)把 用度、分、秒表示,正确的是
A. B. C. D.
(3分)如图,将一幅三角尺叠放在一起,使直角顶点重合于点 ,若 的度数是 ,则 的度数是
A. B. C. D.
二、填空题(共8题,共24分)
(3分)一个棱柱有 个顶点,所有侧棱长的和是 ,则每条侧棱长是 .
(3分)如图,把弯曲的河道改直,能够缩短航程.请你用数学知识解释出现这一现象的原因: .
(3分)如图所示,, 是线段 上任意两点, 是 的中点, 是 的中点,若 ,,则 的长为 .
(3分)【例 】小明晚上放学到家时,钟表的时间显示为 点 分(如图),此时时钟的分针与时针所成角的度数是 .
(3分)如图,点 在直线 上,射线 平分 ,若 ,则 的度数为 度.
(3分)如图,已知 ,以点 为圆心,任意长度为半径画弧,分别交 , 于点 ,,再以点 为圆心, 的长为半径画弧,两弧交于点 ,画射线 .若 ,则 的度数为 .
(3分)如图,直线 , 相交于点 ,若 , 平分 ,则 .
(3分)如图,已知 ,自 点引射线 ,若 , 与 的平分线所成的角的度数为 .
三、解答题(共8题,共66分)
(8分)如图,,, 平分 ,求 的度数.
(8分)计算:.
(8分)如图,,, 三点在同一直线上, 与 互补.
(1) 与 的度数相等吗,为什么?
(2) 已知 平分 ,若射线 在 的内部,且满足 与 互余;
① ,求 的度数;
②试探究 与 之间有怎样的数量关系,请写出结论并说明理由.
(8分)已知线段 ,点 从点 出发沿射线 以每秒 个单位长度的速度运动,同时点 从点 出发沿射线 以每秒 个单位长度的速度运动,, 分别为 , 的中点,运动的时间为 .
(1) 若 ,,求 的值,并写出此时 , 之间的距离;
(2) 点 , 能否重合为一点,若能,请直接写出此时线段 与线段 之间的数量关系;若不能,说明理由.
(8分)如图,,.
(1) 试说明:.
(2) 若 是 的平分线,,求 的度数.
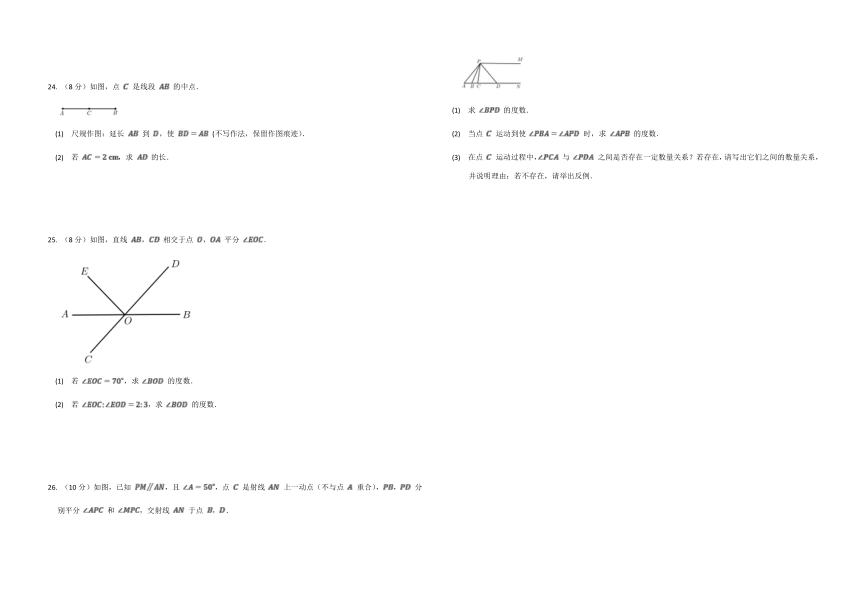
(8分)如图,点 是线段 的中点.
(1) 尺规作图:延长 到 ,使 (不写作法,保留作图痕迹).
(2) 若 ,求 的长.
(8分)如图,直线 , 相交于点 , 平分 .
(1) 若 ,求 的度数.
(2) 若 ,求 的度数.
(10分)如图,已知 ,且 ,点 是射线 上一动点(不与点 重合),, 分别平分 和 ,交射线 于点 ,.
(1) 求 的度数.
(2) 当点 运动到使 时,求 的度数.
(3) 在点 运动过程中, 与 之间是否存在一定数量关系?若存在,请写出它们之间的数量关系,并说明理由;若不存在,请举出反例.
答案
一、选择题(共10题,共30分)
1. 【答案】C
【知识点】面截体
2. 【答案】C
【知识点】两点之间线段最短
3. 【答案】C
【知识点】线段的和差
4. 【答案】D
【知识点】角的概念及表示方法
5. 【答案】C
【解析】A、 与 不互余,故本选项错误;
B、 与 不互余,故本选项错误;
C、 与 互余,故本选项正确;
D、 与 不互余, 和 互补,故本选项错误.
【知识点】余角,补角
6. 【答案】D
【解析】由作图可知:,
所以 .
【知识点】角的计算、作一个角等于已知角
7. 【答案】C
【解析】设这个角为 ,
由题意得:,
解得:,
即这个角是 ,它的补角是 .
【知识点】余角,补角
8. 【答案】D
【解析】 点 在点 北偏西 的方向上,
与西方向的夹角为 ,
又 点 在点 的南偏东 的方向上,
.
【知识点】角的计算、方向角
9. 【答案】A
【解析】方法一:
.
方法二:
【知识点】度分秒的换算
10. 【答案】A
【解析】由题意得 .
,
,
【知识点】角的计算
二、填空题(共8题,共24分)
11. 【答案】
【解析】根据以上分析一个棱柱有 个顶点,所以它是六棱柱,即有 条侧棱,又因为所有侧棱长的和是 ,所以每条侧棱长是 .
故答案为 .
【知识点】认识立体图形
12. 【答案】两点之间线段最短
【知识点】两点之间线段最短
13. 【答案】
【解析】 ,
,,
答: 的长为 .
故答案为:.
【知识点】线段中点的概念及计算、线段的和差
14. 【答案】
【解析】 点 分时,时针与分针相距 份, 点 分时 ,故答案为:.
【知识点】钟面角
15. 【答案】
【解析】因为 平分 ,
所以 ,
所以 .
【知识点】角的计算、角平分线的定义
16. 【答案】
【知识点】作一个角等于已知角
17. 【答案】
【解析】设 ,
则 ,
平分 ,
,
,
,
,
,
.
【知识点】角平分线的定义、角的计算
18. 【答案】 或 .
【解析】若 在 内部,
,
设 ,,
,
,
得 ,
,,
平分 ,
,
.
若 在 外部,
,
设 , ,
,
,
得 ,
,,
平分 ,
,
.
与 的平分线所成的角的度数为 或 .
【知识点】角平分线的定义、角的计算
三、解答题(共8题,共66分)
19. 【答案】 平分 ,且 ,
,
,
.
【知识点】角平分线的定义
20. 【答案】
【知识点】角的计算
21. 【答案】
(1) ,
与 互补,
,
,
.
(2) ① 与 互余,
;
② ,理由如下:
平分 ,
,,
与 互余,
,
,
,
与 互补,
,
,
又 ,
.
【知识点】角的大小比较与计算、角的计算、余角的性质、补角的性质
22. 【答案】
(1) 由题意得,,,
, 分别为 , 的中点,
,,
,,
若 ,,
,
解得: 或 .
当 时,,
当 时,;
综上所述:若 ,,则 时,,或 时,.
(2) 结论:点 , 能重合为一点,此时 ;
理由如下:若点 , 重合为一点,即 ,
,解得 ,
则 ,
此时 .
【知识点】绝对值的几何意义、线段的和差
23. 【答案】
(1) ,
,
,
,
.
(2) 且 ,
,
是 的平分线,
,
,
.
【知识点】内错角相等、角平分线的定义、同旁内角互补、同位角相等
24. 【答案】
(1)
(2) 点 是线段 的中点,,
,
,
.
【知识点】作相等线段、线段的和差、线段中点的概念及计算
25. 【答案】
(1) 平分 ,
,
.
(2) 设 ,,
根据题意得 ,解得 ,
,
,
.
【知识点】对顶角的性质、角平分线的定义、角的计算
26. 【答案】
(1) ,
,
,
,
, 分别平分 和 ,
,,
.
(2) ,
,
,
,
,
由()得:,,
.
(3) ,
,,
平分 ,
,
.
【知识点】角平分线的定义、同旁内角互补、内错角相等
(共26题,共120分)
一、选择题(共10题,共30分)
(3分)用一个平面去截一个正方体,截面可能是
A.七边形 B.圆 C.长方形 D.圆锥
(3分)如图,小军同学用小刀沿虚线将一半圆形纸片剪掉右上角,发现剩下图形的周长比原半圆形的周长要小,能正确解释这一现象的数学知识是
A.经过两点有且只有一条直线 B.经过一点有无数条直线
C.两点之间,线段最短 D.部分小于总体
(3分)已知点 ,, 在同一条直线上,若线段 ,,,则下列判断正确的是
A.点 在线段 上 B.点 在线段 上
C.点 在线段 上 D.点 在线段 的延长线上
(3分)如图,能用 ,, 三种方法表示同一个角的图形是
A. B.
C. D.
(3分)将一副三角板按如图所示位置摆放,其中 与 一定互余的是
A.
B.
C.
D.
(3分)如图,已知 ,,分别以 , 为圆心,以同样长为半径作弧,交 , 于点 ,,交 , 于点 ,;以点 为圆心,以 长为半径作弧,交 于点 ,作射线 ,则 的度数是
A. B. C. D.
(3分)一个角的余角是 ,则这个角的补角是
A. B. C. D.
(3分)如图,若点 在点 北偏西 的方向上,点 在点 的南偏东 的方向上,则 (小于平角)的度数等于
A. B. C. D.
(3分)把 用度、分、秒表示,正确的是
A. B. C. D.
(3分)如图,将一幅三角尺叠放在一起,使直角顶点重合于点 ,若 的度数是 ,则 的度数是
A. B. C. D.
二、填空题(共8题,共24分)
(3分)一个棱柱有 个顶点,所有侧棱长的和是 ,则每条侧棱长是 .
(3分)如图,把弯曲的河道改直,能够缩短航程.请你用数学知识解释出现这一现象的原因: .
(3分)如图所示,, 是线段 上任意两点, 是 的中点, 是 的中点,若 ,,则 的长为 .
(3分)【例 】小明晚上放学到家时,钟表的时间显示为 点 分(如图),此时时钟的分针与时针所成角的度数是 .
(3分)如图,点 在直线 上,射线 平分 ,若 ,则 的度数为 度.
(3分)如图,已知 ,以点 为圆心,任意长度为半径画弧,分别交 , 于点 ,,再以点 为圆心, 的长为半径画弧,两弧交于点 ,画射线 .若 ,则 的度数为 .
(3分)如图,直线 , 相交于点 ,若 , 平分 ,则 .
(3分)如图,已知 ,自 点引射线 ,若 , 与 的平分线所成的角的度数为 .
三、解答题(共8题,共66分)
(8分)如图,,, 平分 ,求 的度数.
(8分)计算:.
(8分)如图,,, 三点在同一直线上, 与 互补.
(1) 与 的度数相等吗,为什么?
(2) 已知 平分 ,若射线 在 的内部,且满足 与 互余;
① ,求 的度数;
②试探究 与 之间有怎样的数量关系,请写出结论并说明理由.
(8分)已知线段 ,点 从点 出发沿射线 以每秒 个单位长度的速度运动,同时点 从点 出发沿射线 以每秒 个单位长度的速度运动,, 分别为 , 的中点,运动的时间为 .
(1) 若 ,,求 的值,并写出此时 , 之间的距离;
(2) 点 , 能否重合为一点,若能,请直接写出此时线段 与线段 之间的数量关系;若不能,说明理由.
(8分)如图,,.
(1) 试说明:.
(2) 若 是 的平分线,,求 的度数.
(8分)如图,点 是线段 的中点.
(1) 尺规作图:延长 到 ,使 (不写作法,保留作图痕迹).
(2) 若 ,求 的长.
(8分)如图,直线 , 相交于点 , 平分 .
(1) 若 ,求 的度数.
(2) 若 ,求 的度数.
(10分)如图,已知 ,且 ,点 是射线 上一动点(不与点 重合),, 分别平分 和 ,交射线 于点 ,.
(1) 求 的度数.
(2) 当点 运动到使 时,求 的度数.
(3) 在点 运动过程中, 与 之间是否存在一定数量关系?若存在,请写出它们之间的数量关系,并说明理由;若不存在,请举出反例.
答案
一、选择题(共10题,共30分)
1. 【答案】C
【知识点】面截体
2. 【答案】C
【知识点】两点之间线段最短
3. 【答案】C
【知识点】线段的和差
4. 【答案】D
【知识点】角的概念及表示方法
5. 【答案】C
【解析】A、 与 不互余,故本选项错误;
B、 与 不互余,故本选项错误;
C、 与 互余,故本选项正确;
D、 与 不互余, 和 互补,故本选项错误.
【知识点】余角,补角
6. 【答案】D
【解析】由作图可知:,
所以 .
【知识点】角的计算、作一个角等于已知角
7. 【答案】C
【解析】设这个角为 ,
由题意得:,
解得:,
即这个角是 ,它的补角是 .
【知识点】余角,补角
8. 【答案】D
【解析】 点 在点 北偏西 的方向上,
与西方向的夹角为 ,
又 点 在点 的南偏东 的方向上,
.
【知识点】角的计算、方向角
9. 【答案】A
【解析】方法一:
.
方法二:
【知识点】度分秒的换算
10. 【答案】A
【解析】由题意得 .
,
,
【知识点】角的计算
二、填空题(共8题,共24分)
11. 【答案】
【解析】根据以上分析一个棱柱有 个顶点,所以它是六棱柱,即有 条侧棱,又因为所有侧棱长的和是 ,所以每条侧棱长是 .
故答案为 .
【知识点】认识立体图形
12. 【答案】两点之间线段最短
【知识点】两点之间线段最短
13. 【答案】
【解析】 ,
,,
答: 的长为 .
故答案为:.
【知识点】线段中点的概念及计算、线段的和差
14. 【答案】
【解析】 点 分时,时针与分针相距 份, 点 分时 ,故答案为:.
【知识点】钟面角
15. 【答案】
【解析】因为 平分 ,
所以 ,
所以 .
【知识点】角的计算、角平分线的定义
16. 【答案】
【知识点】作一个角等于已知角
17. 【答案】
【解析】设 ,
则 ,
平分 ,
,
,
,
,
,
.
【知识点】角平分线的定义、角的计算
18. 【答案】 或 .
【解析】若 在 内部,
,
设 ,,
,
,
得 ,
,,
平分 ,
,
.
若 在 外部,
,
设 , ,
,
,
得 ,
,,
平分 ,
,
.
与 的平分线所成的角的度数为 或 .
【知识点】角平分线的定义、角的计算
三、解答题(共8题,共66分)
19. 【答案】 平分 ,且 ,
,
,
.
【知识点】角平分线的定义
20. 【答案】
【知识点】角的计算
21. 【答案】
(1) ,
与 互补,
,
,
.
(2) ① 与 互余,
;
② ,理由如下:
平分 ,
,,
与 互余,
,
,
,
与 互补,
,
,
又 ,
.
【知识点】角的大小比较与计算、角的计算、余角的性质、补角的性质
22. 【答案】
(1) 由题意得,,,
, 分别为 , 的中点,
,,
,,
若 ,,
,
解得: 或 .
当 时,,
当 时,;
综上所述:若 ,,则 时,,或 时,.
(2) 结论:点 , 能重合为一点,此时 ;
理由如下:若点 , 重合为一点,即 ,
,解得 ,
则 ,
此时 .
【知识点】绝对值的几何意义、线段的和差
23. 【答案】
(1) ,
,
,
,
.
(2) 且 ,
,
是 的平分线,
,
,
.
【知识点】内错角相等、角平分线的定义、同旁内角互补、同位角相等
24. 【答案】
(1)
(2) 点 是线段 的中点,,
,
,
.
【知识点】作相等线段、线段的和差、线段中点的概念及计算
25. 【答案】
(1) 平分 ,
,
.
(2) 设 ,,
根据题意得 ,解得 ,
,
,
.
【知识点】对顶角的性质、角平分线的定义、角的计算
26. 【答案】
(1) ,
,
,
,
, 分别平分 和 ,
,,
.
(2) ,
,
,
,
,
由()得:,,
.
(3) ,
,,
平分 ,
,
.
【知识点】角平分线的定义、同旁内角互补、内错角相等
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
