第6章图形的相似——相似三角形综合复习 无答案 苏科版数学九年级下册
文档属性
| 名称 | 第6章图形的相似——相似三角形综合复习 无答案 苏科版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 378.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 00:00:00 | ||
图片预览

文档简介
九年级培优相似三角形复习(白银级)
【知识点】
1.黄金分割点:,比值约为0.618,这个比值称为黄金比.
注意:(1)一条线段的黄金分割点有两个,它们关于中点中心对称;
(2)黄金三角形:顶角为36°的等腰三角形
2.相似三角形判定:(1)两个角相等 (2)两边对应成比例且夹角相等
(3)三边对应成比例 (4)平行即相似(“A”字型,“8”字型,相似常用辅助线平行线)
3.两个三角形相似,对应边之比,高之比,中线之比,周长之比=相似比,面积比等于相似比的平方(当同高时,底之比等于面积比)
4.位似有关性质:(分同侧异侧)
(1)两个位似形一定是相似形;
(2)各对对应顶点所在的直线都经过位似中心;
(3)对应边互相平行(或在同一直线);
(4)各对对应顶点到位似中心的距离的比等于相似比
一.填空题
1.如图,等腰直角的直角边长为3,为斜边上一点,且为上一点,若,则的长为
如图,在边长为9的正方形中,为上一点,连接.过点作,交于点,=3,则等于
3.如图,点在反比例函数的图像上,点在反比例函数的图像上,且,则的值为
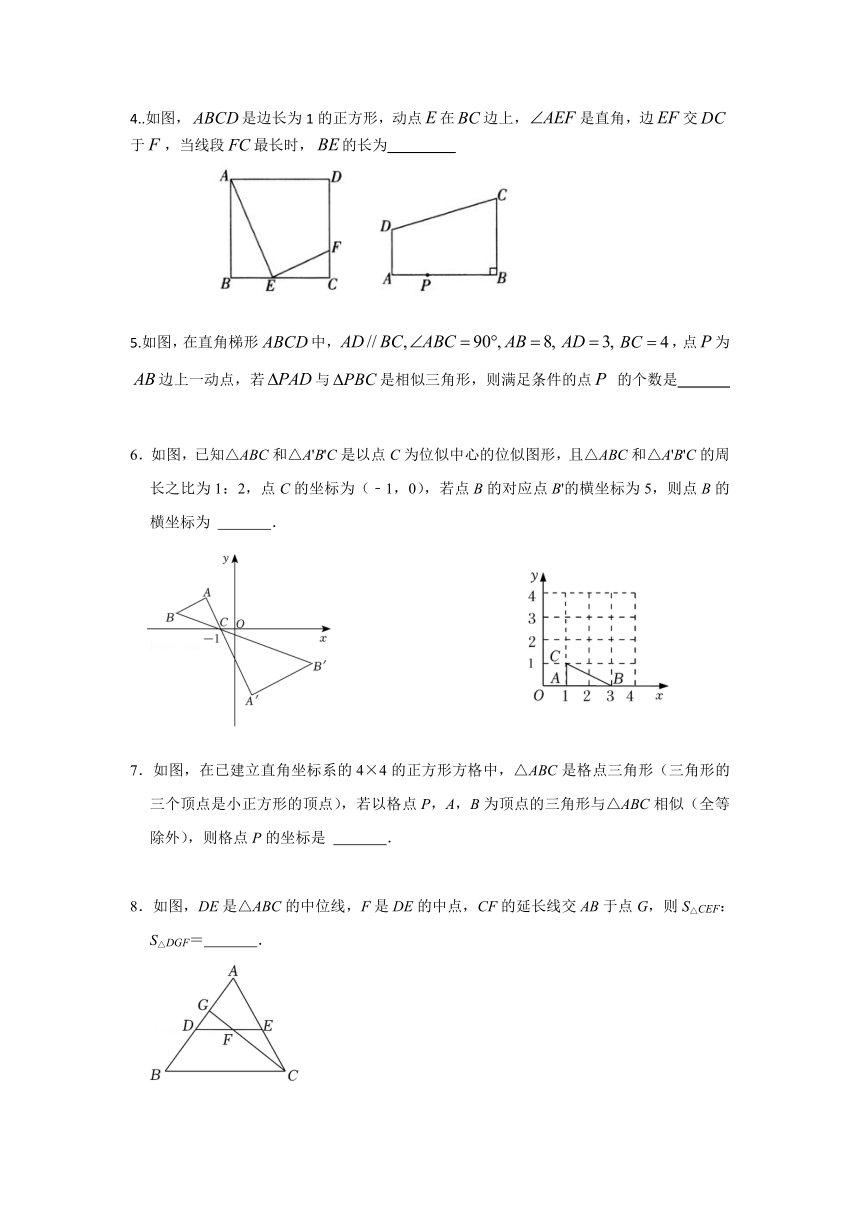
4..如图,是边长为1的正方形,动点在边上,是直角,边交 于,当线段最长时,的长为
5.如图,在直角梯形中,,点为边上一动点,若与是相似三角形,则满足条件的点 的个数是
6.如图,已知△ABC和△A'B'C是以点C为位似中心的位似图形,且△ABC和△A'B'C的周长之比为1:2,点C的坐标为(﹣1,0),若点B的对应点B'的横坐标为5,则点B的横坐标为 .
7.如图,在已建立直角坐标系的4×4的正方形方格中,△ABC是格点三角形(三角形的三个顶点是小正方形的顶点),若以格点P,A,B为顶点的三角形与△ABC相似(全等除外),则格点P的坐标是 .
8.如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则S△CEF:S△DGF= .
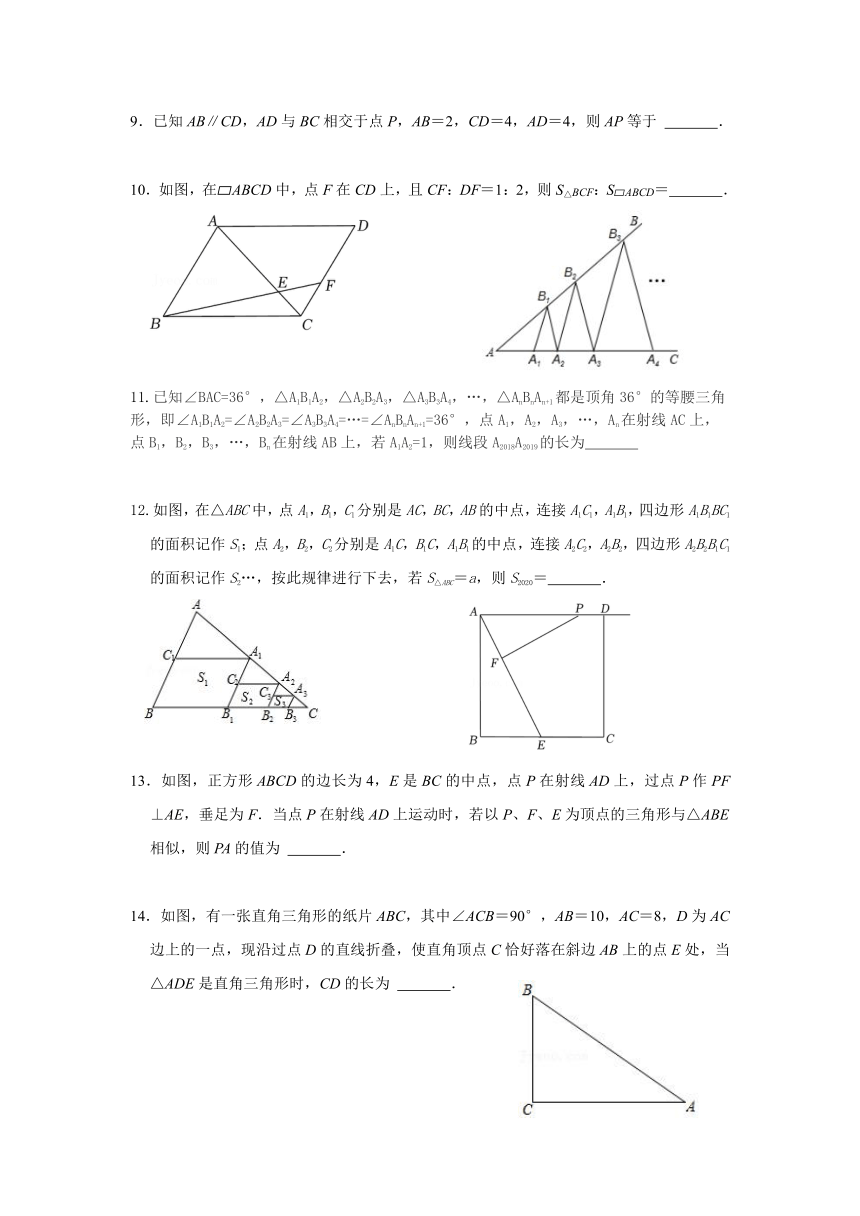
9.已知AB∥CD,AD与BC相交于点P,AB=2,CD=4,AD=4,则AP等于 .
10.如图,在 ABCD中,点F在CD上,且CF:DF=1:2,则S△BCF:S ABCD= .
11.已知∠BAC=36°,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是顶角36°的等腰三角形,即∠A1B1A2=∠A2B2A3=∠A3B3A4=…=∠AnBnAn+1=36°,点A1,A2,A3,…,An在射线AC上,点B1,B2,B3,…,Bn在射线AB上,若A1A2=1,则线段A2018A2019的长为
12.如图,在△ABC中,点A1,B1,C1分别是AC,BC,AB的中点,连接A1C1,A1B1,四边形A1B1BC1的面积记作S1;点A2,B2,C2分别是A1C,B1C,A1B1的中点,连接A2C2,A2B2,四边形A2B2B1C1的面积记作S2…,按此规律进行下去,若S△ABC=a,则S2020= .
13.如图,正方形ABCD的边长为4,E是BC的中点,点P在射线AD上,过点P作PF⊥AE,垂足为F.当点P在射线AD上运动时,若以P、F、E为顶点的三角形与△ABE相似,则PA的值为 .
14.如图,有一张直角三角形的纸片ABC,其中∠ACB=90°,AB=10,AC=8,D为AC边上的一点,现沿过点D的直线折叠,使直角顶点C恰好落在斜边AB上的点E处,当△ADE是直角三角形时,CD的长为 .
二.解答题
1.如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点的坐标分别是A(﹣2,2),B(0,5),C(0,1).
(1)在图1中用无刻度的直尺,以点C为位似中心画△ABC的位似图形,它与△ABC的相似比为1:2(保留作图痕迹,不写作法,画出一种即可);
(2)在图2中平移△ABC,使点A的对应点A1坐标为(2,﹣1),请画出平移后对应的△A1B1C1;
(3)在图2中请用无刻度的直尺在第一、二、四象限内画出一个以A1B1为边,面积是15的矩形A1B1EF(保留作图痕迹,不写作法).
2.在矩形ABCD中,AB=3.点E,F分别在边BC,CD上,
(1)点B,F关于AE所在的直线对称,且E为线段BC的一个四等分点,求线段AD的长度.
(2)已知FC=2,以A,B,E为顶点的三角形与△EFC相似,设BE=a,EC=b,求a,b的关系式.
3.△ABC中,∠BAC是直角,过斜边中点M而垂直于斜边BC的直线交CA的延长线于E,交AB于D,连AM.
求证:(1)△ABC∽△MEC;
(2)AM2=MD ME.
4.如图,在菱形ABCD中,点E在对角线AC上,延长BE交AD于点F.
(1)求证:=;
(2)已知点P在边CD上,请以CP为边,用尺规作一个△CPQ与△AEF相似,并使得点Q在AC上.(只需作出一个△CPQ,保留作图痕迹,不写作法)
5.如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
【知识点】
1.黄金分割点:,比值约为0.618,这个比值称为黄金比.
注意:(1)一条线段的黄金分割点有两个,它们关于中点中心对称;
(2)黄金三角形:顶角为36°的等腰三角形
2.相似三角形判定:(1)两个角相等 (2)两边对应成比例且夹角相等
(3)三边对应成比例 (4)平行即相似(“A”字型,“8”字型,相似常用辅助线平行线)
3.两个三角形相似,对应边之比,高之比,中线之比,周长之比=相似比,面积比等于相似比的平方(当同高时,底之比等于面积比)
4.位似有关性质:(分同侧异侧)
(1)两个位似形一定是相似形;
(2)各对对应顶点所在的直线都经过位似中心;
(3)对应边互相平行(或在同一直线);
(4)各对对应顶点到位似中心的距离的比等于相似比
一.填空题
1.如图,等腰直角的直角边长为3,为斜边上一点,且为上一点,若,则的长为
如图,在边长为9的正方形中,为上一点,连接.过点作,交于点,=3,则等于
3.如图,点在反比例函数的图像上,点在反比例函数的图像上,且,则的值为
4..如图,是边长为1的正方形,动点在边上,是直角,边交 于,当线段最长时,的长为
5.如图,在直角梯形中,,点为边上一动点,若与是相似三角形,则满足条件的点 的个数是
6.如图,已知△ABC和△A'B'C是以点C为位似中心的位似图形,且△ABC和△A'B'C的周长之比为1:2,点C的坐标为(﹣1,0),若点B的对应点B'的横坐标为5,则点B的横坐标为 .
7.如图,在已建立直角坐标系的4×4的正方形方格中,△ABC是格点三角形(三角形的三个顶点是小正方形的顶点),若以格点P,A,B为顶点的三角形与△ABC相似(全等除外),则格点P的坐标是 .
8.如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则S△CEF:S△DGF= .
9.已知AB∥CD,AD与BC相交于点P,AB=2,CD=4,AD=4,则AP等于 .
10.如图,在 ABCD中,点F在CD上,且CF:DF=1:2,则S△BCF:S ABCD= .
11.已知∠BAC=36°,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是顶角36°的等腰三角形,即∠A1B1A2=∠A2B2A3=∠A3B3A4=…=∠AnBnAn+1=36°,点A1,A2,A3,…,An在射线AC上,点B1,B2,B3,…,Bn在射线AB上,若A1A2=1,则线段A2018A2019的长为
12.如图,在△ABC中,点A1,B1,C1分别是AC,BC,AB的中点,连接A1C1,A1B1,四边形A1B1BC1的面积记作S1;点A2,B2,C2分别是A1C,B1C,A1B1的中点,连接A2C2,A2B2,四边形A2B2B1C1的面积记作S2…,按此规律进行下去,若S△ABC=a,则S2020= .
13.如图,正方形ABCD的边长为4,E是BC的中点,点P在射线AD上,过点P作PF⊥AE,垂足为F.当点P在射线AD上运动时,若以P、F、E为顶点的三角形与△ABE相似,则PA的值为 .
14.如图,有一张直角三角形的纸片ABC,其中∠ACB=90°,AB=10,AC=8,D为AC边上的一点,现沿过点D的直线折叠,使直角顶点C恰好落在斜边AB上的点E处,当△ADE是直角三角形时,CD的长为 .
二.解答题
1.如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点的坐标分别是A(﹣2,2),B(0,5),C(0,1).
(1)在图1中用无刻度的直尺,以点C为位似中心画△ABC的位似图形,它与△ABC的相似比为1:2(保留作图痕迹,不写作法,画出一种即可);
(2)在图2中平移△ABC,使点A的对应点A1坐标为(2,﹣1),请画出平移后对应的△A1B1C1;
(3)在图2中请用无刻度的直尺在第一、二、四象限内画出一个以A1B1为边,面积是15的矩形A1B1EF(保留作图痕迹,不写作法).
2.在矩形ABCD中,AB=3.点E,F分别在边BC,CD上,
(1)点B,F关于AE所在的直线对称,且E为线段BC的一个四等分点,求线段AD的长度.
(2)已知FC=2,以A,B,E为顶点的三角形与△EFC相似,设BE=a,EC=b,求a,b的关系式.
3.△ABC中,∠BAC是直角,过斜边中点M而垂直于斜边BC的直线交CA的延长线于E,交AB于D,连AM.
求证:(1)△ABC∽△MEC;
(2)AM2=MD ME.
4.如图,在菱形ABCD中,点E在对角线AC上,延长BE交AD于点F.
(1)求证:=;
(2)已知点P在边CD上,请以CP为边,用尺规作一个△CPQ与△AEF相似,并使得点Q在AC上.(只需作出一个△CPQ,保留作图痕迹,不写作法)
5.如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
