第5章相交线与平行线练习题 含答案 华东师大版七年级数学上册
文档属性
| 名称 | 第5章相交线与平行线练习题 含答案 华东师大版七年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 499.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 15:12:56 | ||
图片预览



文档简介
第5章相交线与平行线练习题华东师大版七年级数学上册
一.选择题
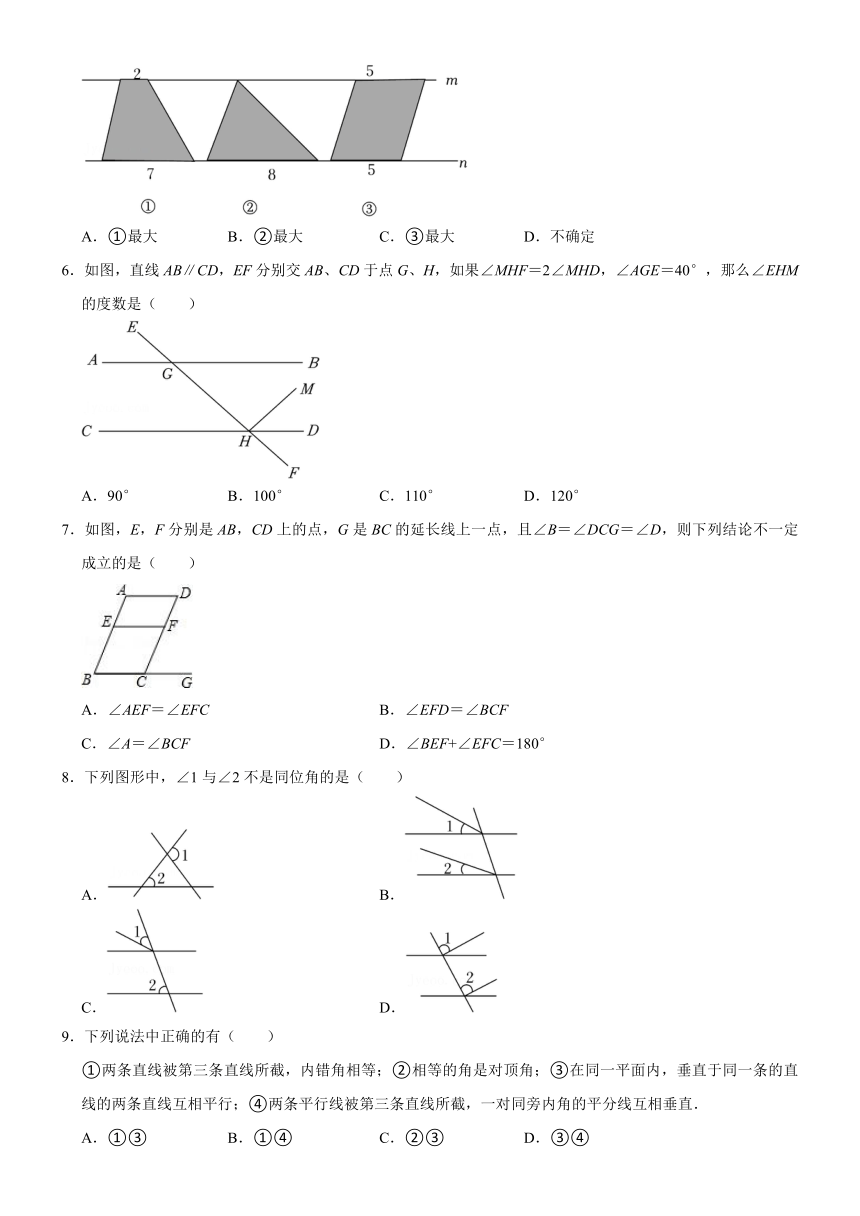
1.如图,线段AB外有一点P过点P作PE⊥AB垂足为E,连接PA、PB,PA=8cm,PB=6cm,PE=4.5cm,若M是线段AB上任意一点,则P到M的最短距离为( )
A.8cm B.6cm C.4.5cm D.无法确定
2.如图,直线a,b被直线c所截,若a∥b,则不正确的是( )
A.∠1+∠3=180° B.∠2+∠3=180° C.∠1=∠4 D.∠2=∠5
3.如图,直线AB∥CD,∠2=50,则∠1的度数是( )
A.120° B.110° C.140° D.130°
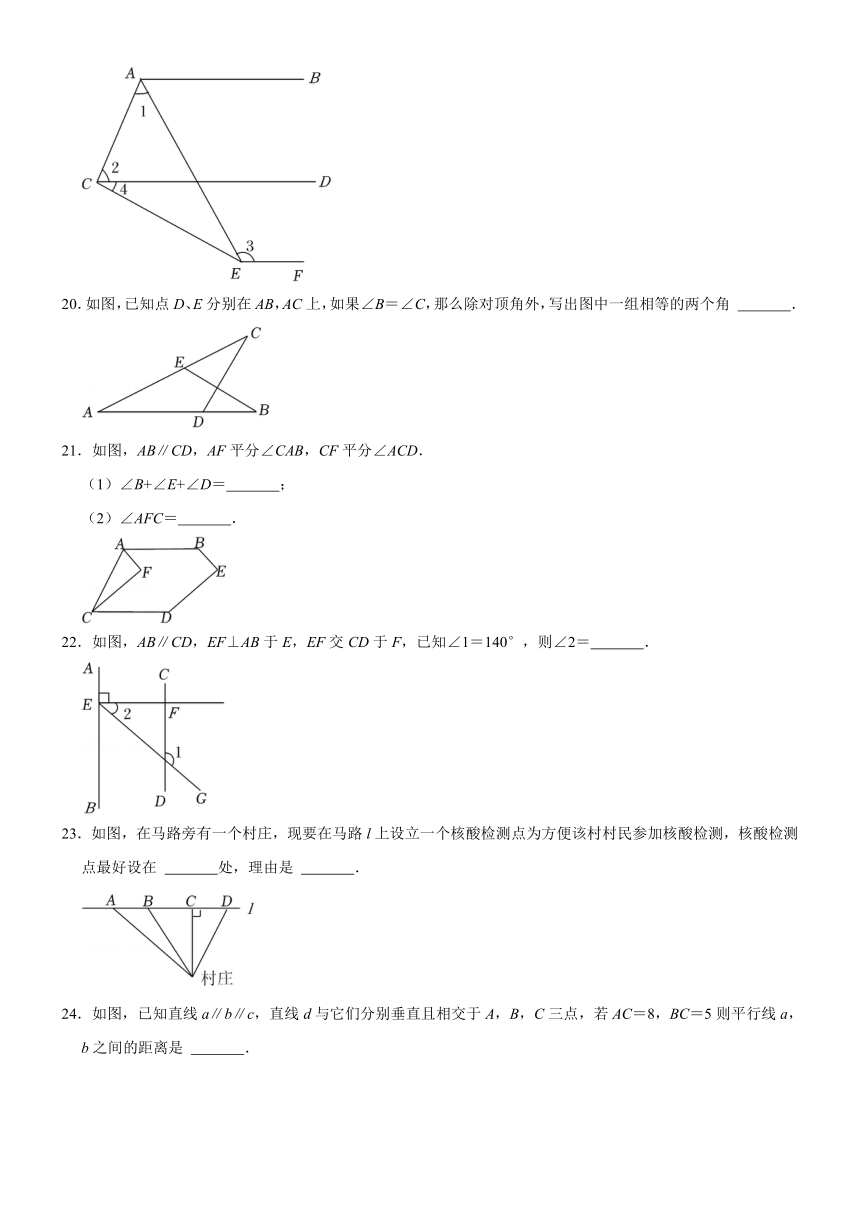
4.如图,AB∥CD,BF交CD于点E,AE⊥BF,∠CEF=35°,则∠A是( )
A.35° B.45° C.55° D.65°
5.如图已知直线m∥n.三个图形的顶点均在直线m,n上,三个图形面积最大的结论正确的是( )
A.①最大 B.②最大 C.③最大 D.不确定
6.如图,直线AB∥CD,EF分别交AB、CD于点G、H,如果∠MHF=2∠MHD,∠AGE=40°,那么∠EHM的度数是( )
A.90° B.100° C.110° D.120°
7.如图,E,F分别是AB,CD上的点,G是BC的延长线上一点,且∠B=∠DCG=∠D,则下列结论不一定成立的是( )
A.∠AEF=∠EFC B.∠EFD=∠BCF
C.∠A=∠BCF D.∠BEF+∠EFC=180°
8.下列图形中,∠1与∠2不是同位角的是( )
A. B.
C. D.
9.下列说法中正确的有( )
①两条直线被第三条直线所截,内错角相等;②相等的角是对顶角;③在同一平面内,垂直于同一条的直线的两条直线互相平行;④两条平行线被第三条直线所截,一对同旁内角的平分线互相垂直.
A.①③ B.①④ C.②③ D.③④
10.小明把一副三角板按如图所示方式摆放,直角边CD与直角边AB相交于点F,斜边DE∥BC,∠B=30°,∠E=45°,则∠CFB的度数是( )
A.95° B.115° C.105° D.125°
11.如图,与∠1是内错角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
12.如图,在下列给出的条件中,不能判定DE∥BC的是( )
A.∠1=∠2 B.∠3=∠4
C.∠5=∠C D.∠B+∠BDE=180°
13.如图,将矩形纸片ABCD沿BD折叠,得到△BDC′,DC′与AB交于点E.若∠1=35°,则∠2的度数为( )
A.20° B.10° C.15° D.25°
14.如图,将一副三角尺按图中所示位置摆放,点F在AC上,AB∥DE,则∠EFC的度数是( )
A.65° B.60° C.70° D.75°
15.如图,AF与BD相交于点C,下列推理错误的是( )
A.∵∠1+∠3=90°,∴AF⊥BD
B.∵CE∥FD,∴∠3+∠4+∠F=180°
C.∵AB∥CE,CE∥FD,∴AB∥FD
D.∵∠2=∠3,∴AB∥CE
二.填空题
16.如图,∠1=∠2,∠DAB=83°,则∠B= 度.
17.如图,在△ABC中,DE∥BC,分别交AB、AC于D、E,且CD⊥BE,CD=3,BE=5,试求BC+DE的值为 .
18.如图,AO⊥BO,CO⊥DO,∠AOC=75°,则∠BOD= .
19.如图已知:AB∥CD,CD∥EF,AE平分∠BAC,AC⊥CE,有下列结论:①AB∥EF;②2∠1﹣∠4=90°;③2∠3﹣∠2=180°;④∠3+∠4=135°.其中,正确的结论有 .(填序号)
20.如图,已知点D、E分别在AB,AC上,如果∠B=∠C,那么除对顶角外,写出图中一组相等的两个角 .
21.如图,AB∥CD,AF平分∠CAB,CF平分∠ACD.
(1)∠B+∠E+∠D= ;
(2)∠AFC= .
22.如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=140°,则∠2= .
23.如图,在马路旁有一个村庄,现要在马路l上设立一个核酸检测点为方便该村村民参加核酸检测,核酸检测点最好设在 处,理由是 .
24.如图,已知直线a∥b∥c,直线d与它们分别垂直且相交于A,B,C三点,若AC=8,BC=5则平行线a,b之间的距离是 .
25.如图,直线l1,l2被直线l3所截,l3分别交l1,l2于点A和点B,过点B的直线l4交l1于点C.若∠1=130°,∠2=60°,∠3=50°,则∠4= .
26.如图,直线l1∥l2,∠1=34°,则∠2与∠3的度数和为 .
27.如图,a∥b,∠1=150°,∠2=90°,则∠3的度数是 °.
28.如图,将一张长方形的纸片沿折痕EF翻折,使点C,D分别落在点M,N的位置.
(1)若∠AEN=20°,则∠AEF的度数为 ;
(2)若∠BFM=∠EFM,则∠DEF的度数为 .
29.如图,二条直线l1与l2相交于点O,l1绕点O逆时针旋转50°得到l3,则∠1+∠2= .
30.光线在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射.如图,在空气中平行的两条入射光线,在水中的两条折射光线也是平行的.若水面和杯底互相平行,且∠1=132°,则∠2= .
三.解答题
31.完善证明过程:请在横线上填写结论并在括号中注明理由.
已知:如图,∠1+∠2=180°,∠3=∠4.
求证:EF∥GH.
证明:
∵∠1+∠2=180°(已知)
∠BEG=∠1 ( )
∴∠BEG+∠ =180°(等量代换)
∴AB∥CD ( )
∴∠BEG=∠EGC ( )
∵∠3=∠4 ( )
∴∠3+∠ =∠4+∠EGC(等式的性质)
即∠FEG=∠
∴EF∥GH ( )
32.如图,已知∠1=∠2,CD、EF分别是∠ACB、∠AED的平分线.求证:BC∥DE.
33.如图,AD既是△ABC的高也是它的角平分线,点G在线段BD上,过点G作EG⊥BC,交CA的延长线于点E,∠E与∠AFE相等吗?为什么?
34.如图,点B、C在直线AD上,∠DCG=70°,BF平分∠DBE,CG∥BF,求∠ABE的度数.
35.看图填空:(请将不完整的解题过程及根据补充完整)
已知:如图,AB∥CD,BC平分∠ABD,∠1=50°,求∠2的度数.
解:因为AB∥CD,∠1=50°,
根据
所以∠ABC=∠1=50°.
又因为BC平分∠ABD,∠ABC=50°
所以 =∠ABC=50°.
根据“两直线平行,同旁内角补”.
所以∠ABD+ =180°
所以∠CDB=180°﹣∠ABD=80°.
根据 ,
所以∠2=∠CDB=80°
第5章相交线与平行线练习题---吉林省榆树市八号镇第一中学2022-2023学年华东师大版七年级数学上册
一.选择题
1. C.2. D.3. D.4. C.5. C.6. B.7. B.8. B.9. D.10. C.11. B.12. B.13. A.14. D.15. D.
二.填空题
16.如图,∠1=∠2,∠DAB=83°,则∠B= 97 度.
17.如图,在△ABC中,DE∥BC,分别交AB、AC于D、E,且CD⊥BE,CD=3,BE=5,试求BC+DE的值为 .
18.如图,AO⊥BO,CO⊥DO,∠AOC=75°,则∠BOD= 105° .
19.如图已知:AB∥CD,CD∥EF,AE平分∠BAC,AC⊥CE,有下列结论:①AB∥EF;②2∠1﹣∠4=90°;③2∠3﹣∠2=180°;④∠3+∠4=135°.其中,正确的结论有 ①②③④ .(填序号)
20.如图,已知点D、E分别在AB,AC上,如果∠B=∠C,那么除对顶角外,写出图中一组相等的两个角 ∠BDO=∠CEO或∠ADC=∠AEB .
21.如图,AB∥CD,AF平分∠CAB,CF平分∠ACD.
(1)∠B+∠E+∠D= 360° ;
(2)∠AFC= 90° .
22.如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=140°,则∠2= 50° .
23.如图,在马路旁有一个村庄,现要在马路l上设立一个核酸检测点为方便该村村民参加核酸检测,核酸检测点最好设在 点C 处,理由是 垂线段最短 .
24.如图,已知直线a∥b∥c,直线d与它们分别垂直且相交于A,B,C三点,若AC=8,BC=5则平行线a,b之间的距离是 3 .
25.如图,直线l1,l2被直线l3所截,l3分别交l1,l2于点A和点B,过点B的直线l4交l1于点C.若∠1=130°,∠2=60°,∠3=50°,则∠4= 70° .
26.如图,直线l1∥l2,∠1=34°,则∠2与∠3的度数和为 214° .
27.如图,a∥b,∠1=150°,∠2=90°,则∠3的度数是 120 °.
28.如图,将一张长方形的纸片沿折痕EF翻折,使点C,D分别落在点M,N的位置.
(1)若∠AEN=20°,则∠AEF的度数为 80° ;
(2)若∠BFM=∠EFM,则∠DEF的度数为 108° .
29.如图,二条直线l1与l2相交于点O,l1绕点O逆时针旋转50°得到l3,则∠1+∠2= 130°. .
30.光线在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射.如图,在空气中平行的两条入射光线,在水中的两条折射光线也是平行的.若水面和杯底互相平行,且∠1=132°,则∠2= 48° .
三.解答题
31.
证明:∵∠1+∠2=180°(已知),∠BEG=∠1(对顶角相等),
∴∠BEG+∠2=180°,
∴AB∥CD(同旁内角互补,两直线平行),
∴∠BEG=∠EGC(两直线平行,内错角相等),
∵∠3=∠4(已知),
∴∠3+∠BEG=∠4+∠EGC(等式性质),
即∠FEG=∠HGE,
∴EF∥GH,
32.
证明:∵∠1=∠2,
∴EF∥CD,
∴∠3=∠4,
∵CD、EF分别是∠ACB、∠AED的平分线,
∴∠ACB=2∠3,∠AED=2∠4,
∴∠AED=∠ACB,
∴BC∥DE.
33.
解:∠E=∠AFE,
理由如下:
∵AD既是△ABC的高也是它的角平分线,
∴AD⊥BC,∠BAD=∠CAD,
∵EG⊥BC,
∴AD∥EG,
∴∠CAD=∠E,∠BAD=∠AFE,
∴∠E=∠AFE.
34.
解:∵CG∥BF,
∴∠DCG=∠CBF,
∵∠DCG=70°,
∴∠DCG=∠CBF,
∵BF平分∠DBE,
∴∠CBE=2∠CBF=140°,
∴∠ABE=180°﹣∠CBE=180°﹣140°=40°.
35.
解:因为AB∥CD,∠1=50°,
所以∠ABC=∠1=50°(两直线平行,同位角相等),
又因为BC平分∠ABD,∠ABC=50°,
所以∠CBD=∠ABC=50°(角平分线的定义),
又因为AB∥CD,
所以∠ABD+∠CDB=180°(两直线平行,同旁内角互补),
所以∠CDB=180°﹣∠ABD=80°,
所以∠2=∠CDB=80°(对顶角相等).
故答案为:两直线平行,同位角相等;∠CBD,∠CDB;对顶角相等.
一.选择题
1.如图,线段AB外有一点P过点P作PE⊥AB垂足为E,连接PA、PB,PA=8cm,PB=6cm,PE=4.5cm,若M是线段AB上任意一点,则P到M的最短距离为( )
A.8cm B.6cm C.4.5cm D.无法确定
2.如图,直线a,b被直线c所截,若a∥b,则不正确的是( )
A.∠1+∠3=180° B.∠2+∠3=180° C.∠1=∠4 D.∠2=∠5
3.如图,直线AB∥CD,∠2=50,则∠1的度数是( )
A.120° B.110° C.140° D.130°
4.如图,AB∥CD,BF交CD于点E,AE⊥BF,∠CEF=35°,则∠A是( )
A.35° B.45° C.55° D.65°
5.如图已知直线m∥n.三个图形的顶点均在直线m,n上,三个图形面积最大的结论正确的是( )
A.①最大 B.②最大 C.③最大 D.不确定
6.如图,直线AB∥CD,EF分别交AB、CD于点G、H,如果∠MHF=2∠MHD,∠AGE=40°,那么∠EHM的度数是( )
A.90° B.100° C.110° D.120°
7.如图,E,F分别是AB,CD上的点,G是BC的延长线上一点,且∠B=∠DCG=∠D,则下列结论不一定成立的是( )
A.∠AEF=∠EFC B.∠EFD=∠BCF
C.∠A=∠BCF D.∠BEF+∠EFC=180°
8.下列图形中,∠1与∠2不是同位角的是( )
A. B.
C. D.
9.下列说法中正确的有( )
①两条直线被第三条直线所截,内错角相等;②相等的角是对顶角;③在同一平面内,垂直于同一条的直线的两条直线互相平行;④两条平行线被第三条直线所截,一对同旁内角的平分线互相垂直.
A.①③ B.①④ C.②③ D.③④
10.小明把一副三角板按如图所示方式摆放,直角边CD与直角边AB相交于点F,斜边DE∥BC,∠B=30°,∠E=45°,则∠CFB的度数是( )
A.95° B.115° C.105° D.125°
11.如图,与∠1是内错角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
12.如图,在下列给出的条件中,不能判定DE∥BC的是( )
A.∠1=∠2 B.∠3=∠4
C.∠5=∠C D.∠B+∠BDE=180°
13.如图,将矩形纸片ABCD沿BD折叠,得到△BDC′,DC′与AB交于点E.若∠1=35°,则∠2的度数为( )
A.20° B.10° C.15° D.25°
14.如图,将一副三角尺按图中所示位置摆放,点F在AC上,AB∥DE,则∠EFC的度数是( )
A.65° B.60° C.70° D.75°
15.如图,AF与BD相交于点C,下列推理错误的是( )
A.∵∠1+∠3=90°,∴AF⊥BD
B.∵CE∥FD,∴∠3+∠4+∠F=180°
C.∵AB∥CE,CE∥FD,∴AB∥FD
D.∵∠2=∠3,∴AB∥CE
二.填空题
16.如图,∠1=∠2,∠DAB=83°,则∠B= 度.
17.如图,在△ABC中,DE∥BC,分别交AB、AC于D、E,且CD⊥BE,CD=3,BE=5,试求BC+DE的值为 .
18.如图,AO⊥BO,CO⊥DO,∠AOC=75°,则∠BOD= .
19.如图已知:AB∥CD,CD∥EF,AE平分∠BAC,AC⊥CE,有下列结论:①AB∥EF;②2∠1﹣∠4=90°;③2∠3﹣∠2=180°;④∠3+∠4=135°.其中,正确的结论有 .(填序号)
20.如图,已知点D、E分别在AB,AC上,如果∠B=∠C,那么除对顶角外,写出图中一组相等的两个角 .
21.如图,AB∥CD,AF平分∠CAB,CF平分∠ACD.
(1)∠B+∠E+∠D= ;
(2)∠AFC= .
22.如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=140°,则∠2= .
23.如图,在马路旁有一个村庄,现要在马路l上设立一个核酸检测点为方便该村村民参加核酸检测,核酸检测点最好设在 处,理由是 .
24.如图,已知直线a∥b∥c,直线d与它们分别垂直且相交于A,B,C三点,若AC=8,BC=5则平行线a,b之间的距离是 .
25.如图,直线l1,l2被直线l3所截,l3分别交l1,l2于点A和点B,过点B的直线l4交l1于点C.若∠1=130°,∠2=60°,∠3=50°,则∠4= .
26.如图,直线l1∥l2,∠1=34°,则∠2与∠3的度数和为 .
27.如图,a∥b,∠1=150°,∠2=90°,则∠3的度数是 °.
28.如图,将一张长方形的纸片沿折痕EF翻折,使点C,D分别落在点M,N的位置.
(1)若∠AEN=20°,则∠AEF的度数为 ;
(2)若∠BFM=∠EFM,则∠DEF的度数为 .
29.如图,二条直线l1与l2相交于点O,l1绕点O逆时针旋转50°得到l3,则∠1+∠2= .
30.光线在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射.如图,在空气中平行的两条入射光线,在水中的两条折射光线也是平行的.若水面和杯底互相平行,且∠1=132°,则∠2= .
三.解答题
31.完善证明过程:请在横线上填写结论并在括号中注明理由.
已知:如图,∠1+∠2=180°,∠3=∠4.
求证:EF∥GH.
证明:
∵∠1+∠2=180°(已知)
∠BEG=∠1 ( )
∴∠BEG+∠ =180°(等量代换)
∴AB∥CD ( )
∴∠BEG=∠EGC ( )
∵∠3=∠4 ( )
∴∠3+∠ =∠4+∠EGC(等式的性质)
即∠FEG=∠
∴EF∥GH ( )
32.如图,已知∠1=∠2,CD、EF分别是∠ACB、∠AED的平分线.求证:BC∥DE.
33.如图,AD既是△ABC的高也是它的角平分线,点G在线段BD上,过点G作EG⊥BC,交CA的延长线于点E,∠E与∠AFE相等吗?为什么?
34.如图,点B、C在直线AD上,∠DCG=70°,BF平分∠DBE,CG∥BF,求∠ABE的度数.
35.看图填空:(请将不完整的解题过程及根据补充完整)
已知:如图,AB∥CD,BC平分∠ABD,∠1=50°,求∠2的度数.
解:因为AB∥CD,∠1=50°,
根据
所以∠ABC=∠1=50°.
又因为BC平分∠ABD,∠ABC=50°
所以 =∠ABC=50°.
根据“两直线平行,同旁内角补”.
所以∠ABD+ =180°
所以∠CDB=180°﹣∠ABD=80°.
根据 ,
所以∠2=∠CDB=80°
第5章相交线与平行线练习题---吉林省榆树市八号镇第一中学2022-2023学年华东师大版七年级数学上册
一.选择题
1. C.2. D.3. D.4. C.5. C.6. B.7. B.8. B.9. D.10. C.11. B.12. B.13. A.14. D.15. D.
二.填空题
16.如图,∠1=∠2,∠DAB=83°,则∠B= 97 度.
17.如图,在△ABC中,DE∥BC,分别交AB、AC于D、E,且CD⊥BE,CD=3,BE=5,试求BC+DE的值为 .
18.如图,AO⊥BO,CO⊥DO,∠AOC=75°,则∠BOD= 105° .
19.如图已知:AB∥CD,CD∥EF,AE平分∠BAC,AC⊥CE,有下列结论:①AB∥EF;②2∠1﹣∠4=90°;③2∠3﹣∠2=180°;④∠3+∠4=135°.其中,正确的结论有 ①②③④ .(填序号)
20.如图,已知点D、E分别在AB,AC上,如果∠B=∠C,那么除对顶角外,写出图中一组相等的两个角 ∠BDO=∠CEO或∠ADC=∠AEB .
21.如图,AB∥CD,AF平分∠CAB,CF平分∠ACD.
(1)∠B+∠E+∠D= 360° ;
(2)∠AFC= 90° .
22.如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=140°,则∠2= 50° .
23.如图,在马路旁有一个村庄,现要在马路l上设立一个核酸检测点为方便该村村民参加核酸检测,核酸检测点最好设在 点C 处,理由是 垂线段最短 .
24.如图,已知直线a∥b∥c,直线d与它们分别垂直且相交于A,B,C三点,若AC=8,BC=5则平行线a,b之间的距离是 3 .
25.如图,直线l1,l2被直线l3所截,l3分别交l1,l2于点A和点B,过点B的直线l4交l1于点C.若∠1=130°,∠2=60°,∠3=50°,则∠4= 70° .
26.如图,直线l1∥l2,∠1=34°,则∠2与∠3的度数和为 214° .
27.如图,a∥b,∠1=150°,∠2=90°,则∠3的度数是 120 °.
28.如图,将一张长方形的纸片沿折痕EF翻折,使点C,D分别落在点M,N的位置.
(1)若∠AEN=20°,则∠AEF的度数为 80° ;
(2)若∠BFM=∠EFM,则∠DEF的度数为 108° .
29.如图,二条直线l1与l2相交于点O,l1绕点O逆时针旋转50°得到l3,则∠1+∠2= 130°. .
30.光线在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射.如图,在空气中平行的两条入射光线,在水中的两条折射光线也是平行的.若水面和杯底互相平行,且∠1=132°,则∠2= 48° .
三.解答题
31.
证明:∵∠1+∠2=180°(已知),∠BEG=∠1(对顶角相等),
∴∠BEG+∠2=180°,
∴AB∥CD(同旁内角互补,两直线平行),
∴∠BEG=∠EGC(两直线平行,内错角相等),
∵∠3=∠4(已知),
∴∠3+∠BEG=∠4+∠EGC(等式性质),
即∠FEG=∠HGE,
∴EF∥GH,
32.
证明:∵∠1=∠2,
∴EF∥CD,
∴∠3=∠4,
∵CD、EF分别是∠ACB、∠AED的平分线,
∴∠ACB=2∠3,∠AED=2∠4,
∴∠AED=∠ACB,
∴BC∥DE.
33.
解:∠E=∠AFE,
理由如下:
∵AD既是△ABC的高也是它的角平分线,
∴AD⊥BC,∠BAD=∠CAD,
∵EG⊥BC,
∴AD∥EG,
∴∠CAD=∠E,∠BAD=∠AFE,
∴∠E=∠AFE.
34.
解:∵CG∥BF,
∴∠DCG=∠CBF,
∵∠DCG=70°,
∴∠DCG=∠CBF,
∵BF平分∠DBE,
∴∠CBE=2∠CBF=140°,
∴∠ABE=180°﹣∠CBE=180°﹣140°=40°.
35.
解:因为AB∥CD,∠1=50°,
所以∠ABC=∠1=50°(两直线平行,同位角相等),
又因为BC平分∠ABD,∠ABC=50°,
所以∠CBD=∠ABC=50°(角平分线的定义),
又因为AB∥CD,
所以∠ABD+∠CDB=180°(两直线平行,同旁内角互补),
所以∠CDB=180°﹣∠ABD=80°,
所以∠2=∠CDB=80°(对顶角相等).
故答案为:两直线平行,同位角相等;∠CBD,∠CDB;对顶角相等.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
