第6单元正比例和反比例能力提升检测卷(单元测试)-小学数学六年级下册苏教版(含答案)
文档属性
| 名称 | 第6单元正比例和反比例能力提升检测卷(单元测试)-小学数学六年级下册苏教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-16 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第6单元正比例和反比例能力提升检测卷(单元测试)-小学数学六年级下册苏教版
一、选择题
1.已知a∶b=4∶5,那么a和b( )。
A.不成比例 B.成反比例 C.成正比例
2.如果5x=y,那么x和y( )。
A.成正比例 B.成反比例 C.不成比例
3.三个量x、y、k(k≠0)的关系是y=kx,当k一定时,x与y这两个量( )。
A.成正比例 B.成反比例 C.不成比例
4.下面图象中,表示和成反比例关系的是( )。
A. B. C.
5.每小时加工20个零件,加工零件的总数与加工时间( )。
A.成正比例 B.成反比例 C.不成比例
6.下面各题中的两个量成正比例的是( )。
A.一个人的身高和他的年龄
B.订《玉林日报》的份数和总钱数
C.要加工的零件总数一定,所需的天数与每天完成的件数
二、填空题
7.每天耕地的公顷数一定,耕地的天数和耕地的公顷数成( )比例。
8.正比例的图像是一条( )。
9.总人数一定,每行站的人数与站的行数成( )比例。
10.如图,在正方形内画一个最大的圆,圈的面积是正方形面积的( )%;圆的周长与正方形周长成( )比例。(填正、反或不成)
11.若3∶m=n∶7,则m和n成( )比例;若=(a,b≠0),则a和b成为( ) 比例。
12.甲、乙两人的速度比是8∶5,已知乙从A地到B地用了40分钟,那么甲行这段路需要用( )分钟。
三、判断题
13.全班人数一定,男生人数和女生人数成反比例。( )
14.A∶10=B(B不为0),A与B成反比例。( )
15.如果和成反比例,和成反比例,那么和也成反比例。( )
16.书院小学米接力赛中,运动员平均速度与他们所用的时间成反比例。( )
17.同一幅条形统计图中,直条长度和所表示的数量成正比例。( )
四、计算题
18.解方程。
x-x= 18%∶= (x+3)÷=19.5 2(x+1)=1-(x-4)
五、解答题
19.一个没拧紧的水龙头,一天要白白浪费掉12千克水。那么,2天、3天、4天……各流掉多少千克水?
(1)把下表填写完整。
天数/天 1 2 3 4 5 6 …
流掉的水量/千克 12 …
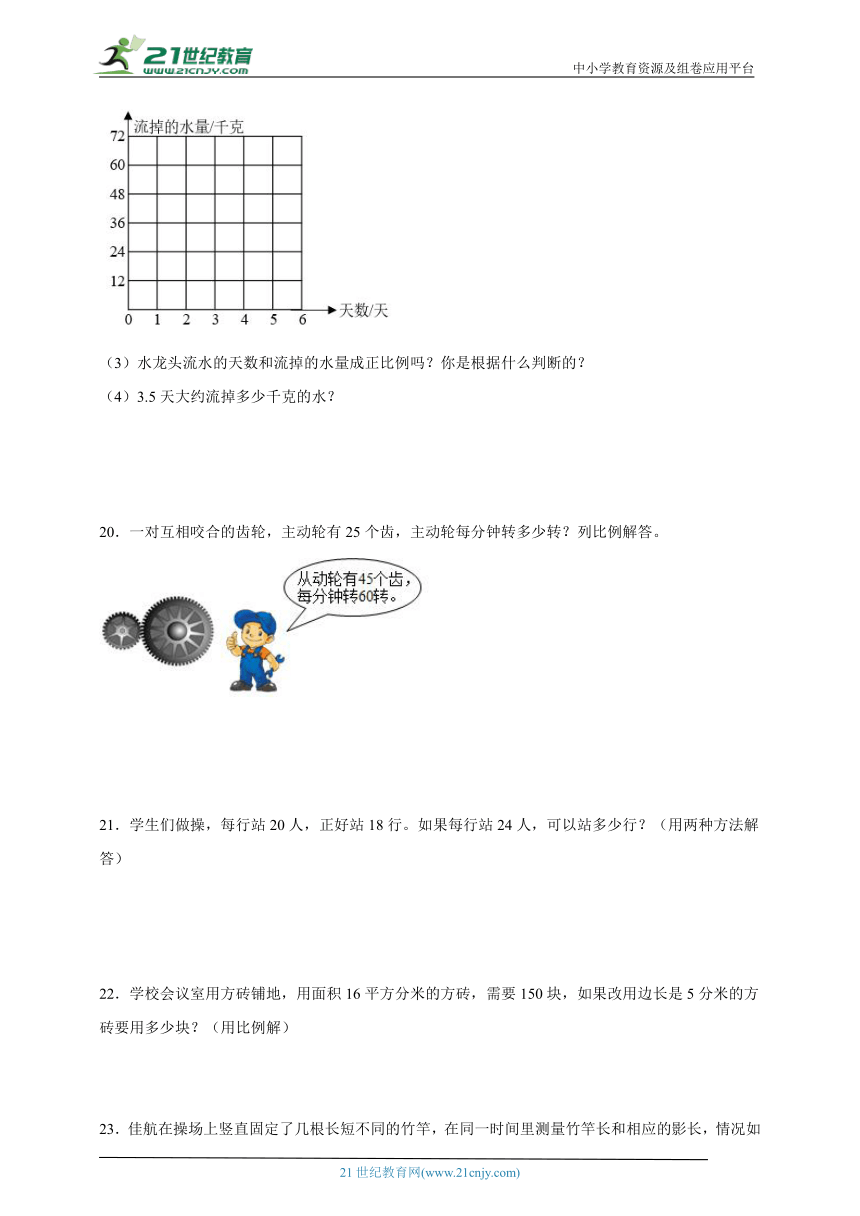
(2)根据表中的数量,在下图中描出天数和流掉的水量的对应点,再把它们按顺序连起来。
(3)水龙头流水的天数和流掉的水量成正比例吗?你是根据什么判断的?
(4)3.5天大约流掉多少千克的水?
20.一对互相咬合的齿轮,主动轮有25个齿,主动轮每分钟转多少转?列比例解答。
21.学生们做操,每行站20人,正好站18行。如果每行站24人,可以站多少行?(用两种方法解答)
22.学校会议室用方砖铺地,用面积16平方分米的方砖,需要150块,如果改用边长是5分米的方砖要用多少块?(用比例解)
23.佳航在操场上竖直固定了几根长短不同的竹竿,在同一时间里测量竹竿长和相应的影长,情况如表:
竹竿长米 1 1.4 1.6 1.8 2.2 3
影长米 0.5 0.7 0.8 0.9 1.1 1.5
这时,佳航身边的强强测量出了旗杆的影长是6米,旗杆的实际高度是多少米?
24.新冠肺炎疫情期间,口罩需求量大幅上升。某工厂接到任务紧急生产一批口罩,下面是每时生产口罩的数量与完成任务总共需要的时间的关系。
每时生产口罩的数量万只 2 3 4 6
时间时 72 48 36 24
(1)每时生产口罩的数量与时间有什么关系?
(2)如果每时生产8万只口罩,那么完成这项任务一共需要多少时?
参考答案:
1.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为a∶b=4∶5(比值一定),所以a和b成正比例。
故答案为:C
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,再做出选择。
2.A
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为5x=y,所以y∶x=5(一定)
是比值一定,所以x和y成正比例;
故答案为:A
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
3.A
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
【详解】因为y=kx,所以=k(一定),x与y成正比例。
三个量x、y、k(k≠0)的关系是y=kx,当k一定时,x与y这两个量成正比例。
故答案为:A
【点睛】熟练掌握正比例意义和辨识,反比例意义和辨识是解答本题的关键。
4.C
【分析】判断两个相关联的量之间成正比例,还是反比例,只要判断出这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;正比例图象由于的值一定,即斜率一定,当x=0时,y也等于0,所以图象是一条从原点出发的射线;成反比例的两个量,一个量随着另一个量的增大而变小,随着另一个量的减小而增大,所以表示反比例观察的图形是一条曲线。据此解答即可。
【详解】成反比例的两个量,一个量随着另一个量的增大而变小,随着另一个量的减小而增大,所以表示反比例观察的图形是一条曲线。
故答案为:C
【点睛】本题是成反比例关系知识的拓展,是把数和形结合起来,研究两个相关联的量之间的关系。
5.A
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
【详解】加工零件总数÷加工时间=每小时加工零件个数,每小时加工20个零件(比值一定),加工零件的总数与加工时间成正比例。
每小时加工20个零件,加工零件的总数与加工时间成正比例。
故答案为:A
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
6.B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】A.一个人的身高和年龄不成比例,通常在生长期,人的身高是随着年龄的增长而增长,但是生长期过了后,骨膜会闭合,停止长高;即人的身高与年龄的比值是不一定的;
B.总钱数÷份数=单价(一定),商一定,所以订《玉林日报》的份数和总钱数成正比例;
C.所需的天数×每天完成的件数=零件总数(一定),乘积一定,所以所需的天数与每天完成的件数成反比例。
故答案为:B
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
7.正
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,否则就不成比例,据此解答即可。
【详解】耕地的公顷数÷耕地的天数=每天耕地的公顷数(一定)
则耕地的天数和耕地的公顷数成正比例。
【点睛】此题属于根据正、反比例的意义,判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断。
8.直线
【分析】两种相关联的量中相对应的两个数的商一定,就成正比例关系,正比例的图像是一条过原点的直径,据此解答。
【详解】根据分析可知,正比例图形是一条直线。
如图:
总价与数量成正比例,图像是一条直线。
【点睛】本题考查正比例意义以及图像的特征。
9.反
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
【详解】因为每行站的人数和站的行数的乘积是总人数,总人数一定,所以每行站的人数和站的行数成反比例。
总人数一定,每行站的人数与站的行数成反比例。
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
10. 78.5 正
【分析】设正方形的边长为a,则正方形的面积是a2。根据圆的面积=πr2,可求出圆的面积是π×(a÷2)2=πa2。用圆的面积除以正方形的面积即可求出圆的面积是正方形面积的百分之几。
圆的周长=πa,正方形的周长=4a,圆的周长÷正方形的周长=πa÷4a=(一定),根据正比例的意义,圆的周长和正方形的周长的商一定,则圆的周长与正方形周长成正比例。
【详解】设正方形的边长和圆的直径为a,则正方形的面积是a2,圆的面积是πa2。
πa2÷a2=π=78.5%,则圆的面积是正方形面积的78.5%。
圆的周长÷正方形的周长=πa÷4a=(一定),则圆的周长与正方形周长成正比例。
【点睛】本题考查正方形和圆的周长、面积,正比例关系的辨认等。用含有字母的式子表示出正方形和圆的周长、面积是解题的关键。
11. 反 正
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例,据此解答。
【详解】3∶m=n∶7
mn=3×7
mn=21(一定),m和n成反比例。
=(a,b≠0)
=(一定),a和b成正比例。
若3∶m=n∶7,则m和n成反比例;若=(a,b≠0),则a和b成为正比例。
【点睛】根据正比例意义以及辨识,反比例意义以及辨识进行解答。
12.25
【分析】根据题意,甲、乙两人的速度比是8∶5,把甲的速度看作是“8”,乙的速度看作是“5”,根据乙从A地到B地用了40分钟,由于距离不变,速度和时间成反比例,甲行驶的路程=乙行驶的路程;设甲行这段路需要x分钟,列比例:8x=5×40,解比例,即可求出甲行这段路需要的时间。
【详解】解:设甲行这段路需要x分钟。
8x=5×40
8x=200
x=200÷8
x=25
甲、乙两人的速度比是8∶5,已知乙从A地到B地用了40分钟,那么甲行这段路需要用25分钟。
【点睛】熟练掌握反比例的意义和辨识是解答本题的关键。
13.×
【分析】根据反比例的意义:两个相关联的量,一个量变化,另一个量也随着变化,如果相对应的两个量x和y的乘积一定,即xy=k(定值),那么这两个量叫做成反比例的量,它们的关系叫做反比例关系;解答即可。
【详解】男生人数+女生人数=全班人数(和一定),不符合反比例意义,原题说法错误。
故答案为:×
【点睛】本题主要考查反比例的意义,解题时要明确:只有乘积一定的两种相关联的两种量,才成反比例。
14.×
【分析】由A∶10=B,可得出=10,符合正比例关系式:=k(一定),由此即可判断。
【详解】由A∶10=B,得出A∶B=10,所以A与B成正比例。
故答案为:×
【点睛】此题主要考查正比例与反比例的意义。
15.×
【分析】判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为和成反比例,所以(一定),则,因为,和成反比例,所以(一定),
把,代入式子(一定),
得出:(一定),是和对应的比值一定,所以和成正比例;
故答案为:×
【点睛】本题主要考查对于正、反比例的辨识。
16.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为运动员平均速度所用时间米(一定),符合反比例的意义,所以在400米赛跑中,运动员平均速度和所用时间成反比例。
故答案为:。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
17.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】直条所表示的数量直条的长度单位直条表示的数量(一定),也就是比值一定,直条的长度与直条所表示的数量成正比例。
故答案为:√
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
18.x=;x=7.8;x=3.6;x=1
【分析】根据等式的性质,方程两边同时除以计算即可;
根据比例的性质,将原来的式子转换成x=18%×6.5,根据等式的性质,方程两边同时除以计算即可;
根据等式的性质,方程两边同时乘,再同时减去3,最后同时除以计算即可;
根据等式的性质,方程两边同时减去x,再同时减去2,最后同时除以3计算即可。
【详解】x-x=
解:x=
x÷=÷
x=
18%∶=
解:x=18%×6.5
x=1.17
x÷=1.17÷
x=7.8
(x+3)÷=19.5
解:(x+3)÷×=19.5×
x+3=3.9
x+3-3=3.9-3
x=0.9
x÷=0.9÷
x=3.6
2(x+1)=1-(x-4)
解:2x+2=1-x+4
2x+2=5-x
2x+2+x=5-x+x
3x+2=5
3x+2-2=5-2
3x=3
3x÷3=3÷3
x=1
19.(1)见详解
(2)见详解
(3)成正比例,利用见详解
(4)42千克
【分析】(1)利用天数乘每天白白流掉的水的质量即可;
(2)根据统计表中的数据,绘制成统计图;
(3)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
(4)用每天流掉的水的质量×3.5天,即可解答。
【详解】(1)2×12=24(千克)
3×12=36(千克)
4×12=48(千克)
5×12=60(千克)
6×12=72(千克)
天数/天 1 2 3 4 5 6 …
流掉的水量/千克 12 24 36 48 60 72 …
(2)图如下:
(3)1÷12=2÷24=3÷36=4÷48=5÷60=6÷72=(一定),水龙头流水的天数和流掉的水量成正比例。
(4)12×3.5=42(千克)
答:3.5天大约流掉42千克的水。
【点睛】解答本题先根据问题从图中找出所需的信息。然后根据数量关系式“天数×每天的流水量=总流水量”即可作出解答。
20.108转
【分析】一对互相咬合的齿轮,说明在旋转过程中,主动轮与从动轮旋转的齿数相等,齿轮的齿数与每分钟旋转的圈数成反比例,设主动轮每分钟转x转;列比例:25x=45×60,解比例,即可解答。
【详解】解:设主动轮每分钟转x转。
25x=45×60
25x=2700
x=2700÷25
x=108
答:主动轮每分钟转108转。
【点睛】解答本题先判断齿轮的齿数与每分钟转的圈数是成什么比例,再列比例进行解答。
21.15行
【分析】第一种方法:原来每行人数×正好站成的行数=做操总人数,做操总人数÷现在每行站的人数=现在可以占的行数;
第二种方法:设可以站x行,总人数=每行站的人数×站成的行数;由于总人数不变,每行站的人数和行数成反比例。现在每行站的人数×现在可以站的行数=原来每行站的人数×正好站成的行数,列方程:24x=20×18,解方程,即可解答。
【详解】第一种:20×18÷24
=360÷24
=15(行)
第二种:解:设可以站x行。
24x=20×18
24x=360
24x÷24=360÷24
x=15
答:可以站15行。
【点睛】解答本题的关键明确总人数不变,利用总人数不变,进行解答。
22.96块
【分析】根据题意可知,会议室的面积是不变的,每一块方砖的面积与所需块数的乘积是一定的,即两种量成反比例;设如果改用边长是5分米的方砖要用x块,列比例:5×5×x=16×150,解比例,即可解答。
【详解】解:设如果改用边长是5分米的方砖要用x块。
5×5×x=16×150
25x=2400
x=2400÷25
x=96
答:如果改用边长是5分米的方砖要用96块。
【点睛】此题首先利用正、反比例的意义判定两种量的关系,解答时关键不要把边长当作面积进行计算。
23.12米
【分析】由于1÷0.5=2,1.4÷0.7=2,1.6÷0.8=2,由此即可知道同一时刻物高与影长成正比,可以设旗杆的实际高度是x米,当竹竿长是1米,影长0.5米时,即旗杆的高度∶旗杆的影长=1∶0.5,据此列出方程,求出未知数的值即可。
【详解】解:设旗杆的实际高度是米,
0.5x=6÷0.5
答:旗杆的实际高度是12米。
【点睛】找出等量关系,是解答此题的关键。
24.(1)成反比例。
(2)18小时
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,由于72×2=48×3=4×36=6×24=144(万只),可知乘积一定,即生产总数量一定,所以每时生产口罩的数量与时间成反比例。
(2)用总共生产的数量除以每时生产的等于一共需要的时间,把数代入即可求解。
【详解】(1)72×2=48×3=36×4=24×6=144(万只)
答:因为每时生产口罩的数量与时间的积一定,所以每时生产口罩的数量与时间成反比例。
(2)144÷8=18(时)
答:完成这项任务一共需要18小时。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第6单元正比例和反比例能力提升检测卷(单元测试)-小学数学六年级下册苏教版
一、选择题
1.已知a∶b=4∶5,那么a和b( )。
A.不成比例 B.成反比例 C.成正比例
2.如果5x=y,那么x和y( )。
A.成正比例 B.成反比例 C.不成比例
3.三个量x、y、k(k≠0)的关系是y=kx,当k一定时,x与y这两个量( )。
A.成正比例 B.成反比例 C.不成比例
4.下面图象中,表示和成反比例关系的是( )。
A. B. C.
5.每小时加工20个零件,加工零件的总数与加工时间( )。
A.成正比例 B.成反比例 C.不成比例
6.下面各题中的两个量成正比例的是( )。
A.一个人的身高和他的年龄
B.订《玉林日报》的份数和总钱数
C.要加工的零件总数一定,所需的天数与每天完成的件数
二、填空题
7.每天耕地的公顷数一定,耕地的天数和耕地的公顷数成( )比例。
8.正比例的图像是一条( )。
9.总人数一定,每行站的人数与站的行数成( )比例。
10.如图,在正方形内画一个最大的圆,圈的面积是正方形面积的( )%;圆的周长与正方形周长成( )比例。(填正、反或不成)
11.若3∶m=n∶7,则m和n成( )比例;若=(a,b≠0),则a和b成为( ) 比例。
12.甲、乙两人的速度比是8∶5,已知乙从A地到B地用了40分钟,那么甲行这段路需要用( )分钟。
三、判断题
13.全班人数一定,男生人数和女生人数成反比例。( )
14.A∶10=B(B不为0),A与B成反比例。( )
15.如果和成反比例,和成反比例,那么和也成反比例。( )
16.书院小学米接力赛中,运动员平均速度与他们所用的时间成反比例。( )
17.同一幅条形统计图中,直条长度和所表示的数量成正比例。( )
四、计算题
18.解方程。
x-x= 18%∶= (x+3)÷=19.5 2(x+1)=1-(x-4)
五、解答题
19.一个没拧紧的水龙头,一天要白白浪费掉12千克水。那么,2天、3天、4天……各流掉多少千克水?
(1)把下表填写完整。
天数/天 1 2 3 4 5 6 …
流掉的水量/千克 12 …
(2)根据表中的数量,在下图中描出天数和流掉的水量的对应点,再把它们按顺序连起来。
(3)水龙头流水的天数和流掉的水量成正比例吗?你是根据什么判断的?
(4)3.5天大约流掉多少千克的水?
20.一对互相咬合的齿轮,主动轮有25个齿,主动轮每分钟转多少转?列比例解答。
21.学生们做操,每行站20人,正好站18行。如果每行站24人,可以站多少行?(用两种方法解答)
22.学校会议室用方砖铺地,用面积16平方分米的方砖,需要150块,如果改用边长是5分米的方砖要用多少块?(用比例解)
23.佳航在操场上竖直固定了几根长短不同的竹竿,在同一时间里测量竹竿长和相应的影长,情况如表:
竹竿长米 1 1.4 1.6 1.8 2.2 3
影长米 0.5 0.7 0.8 0.9 1.1 1.5
这时,佳航身边的强强测量出了旗杆的影长是6米,旗杆的实际高度是多少米?
24.新冠肺炎疫情期间,口罩需求量大幅上升。某工厂接到任务紧急生产一批口罩,下面是每时生产口罩的数量与完成任务总共需要的时间的关系。
每时生产口罩的数量万只 2 3 4 6
时间时 72 48 36 24
(1)每时生产口罩的数量与时间有什么关系?
(2)如果每时生产8万只口罩,那么完成这项任务一共需要多少时?
参考答案:
1.C
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为a∶b=4∶5(比值一定),所以a和b成正比例。
故答案为:C
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,再做出选择。
2.A
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为5x=y,所以y∶x=5(一定)
是比值一定,所以x和y成正比例;
故答案为:A
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
3.A
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
【详解】因为y=kx,所以=k(一定),x与y成正比例。
三个量x、y、k(k≠0)的关系是y=kx,当k一定时,x与y这两个量成正比例。
故答案为:A
【点睛】熟练掌握正比例意义和辨识,反比例意义和辨识是解答本题的关键。
4.C
【分析】判断两个相关联的量之间成正比例,还是反比例,只要判断出这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;正比例图象由于的值一定,即斜率一定,当x=0时,y也等于0,所以图象是一条从原点出发的射线;成反比例的两个量,一个量随着另一个量的增大而变小,随着另一个量的减小而增大,所以表示反比例观察的图形是一条曲线。据此解答即可。
【详解】成反比例的两个量,一个量随着另一个量的增大而变小,随着另一个量的减小而增大,所以表示反比例观察的图形是一条曲线。
故答案为:C
【点睛】本题是成反比例关系知识的拓展,是把数和形结合起来,研究两个相关联的量之间的关系。
5.A
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
【详解】加工零件总数÷加工时间=每小时加工零件个数,每小时加工20个零件(比值一定),加工零件的总数与加工时间成正比例。
每小时加工20个零件,加工零件的总数与加工时间成正比例。
故答案为:A
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
6.B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【详解】A.一个人的身高和年龄不成比例,通常在生长期,人的身高是随着年龄的增长而增长,但是生长期过了后,骨膜会闭合,停止长高;即人的身高与年龄的比值是不一定的;
B.总钱数÷份数=单价(一定),商一定,所以订《玉林日报》的份数和总钱数成正比例;
C.所需的天数×每天完成的件数=零件总数(一定),乘积一定,所以所需的天数与每天完成的件数成反比例。
故答案为:B
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
7.正
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,否则就不成比例,据此解答即可。
【详解】耕地的公顷数÷耕地的天数=每天耕地的公顷数(一定)
则耕地的天数和耕地的公顷数成正比例。
【点睛】此题属于根据正、反比例的意义,判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断。
8.直线
【分析】两种相关联的量中相对应的两个数的商一定,就成正比例关系,正比例的图像是一条过原点的直径,据此解答。
【详解】根据分析可知,正比例图形是一条直线。
如图:
总价与数量成正比例,图像是一条直线。
【点睛】本题考查正比例意义以及图像的特征。
9.反
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
【详解】因为每行站的人数和站的行数的乘积是总人数,总人数一定,所以每行站的人数和站的行数成反比例。
总人数一定,每行站的人数与站的行数成反比例。
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
10. 78.5 正
【分析】设正方形的边长为a,则正方形的面积是a2。根据圆的面积=πr2,可求出圆的面积是π×(a÷2)2=πa2。用圆的面积除以正方形的面积即可求出圆的面积是正方形面积的百分之几。
圆的周长=πa,正方形的周长=4a,圆的周长÷正方形的周长=πa÷4a=(一定),根据正比例的意义,圆的周长和正方形的周长的商一定,则圆的周长与正方形周长成正比例。
【详解】设正方形的边长和圆的直径为a,则正方形的面积是a2,圆的面积是πa2。
πa2÷a2=π=78.5%,则圆的面积是正方形面积的78.5%。
圆的周长÷正方形的周长=πa÷4a=(一定),则圆的周长与正方形周长成正比例。
【点睛】本题考查正方形和圆的周长、面积,正比例关系的辨认等。用含有字母的式子表示出正方形和圆的周长、面积是解题的关键。
11. 反 正
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例,据此解答。
【详解】3∶m=n∶7
mn=3×7
mn=21(一定),m和n成反比例。
=(a,b≠0)
=(一定),a和b成正比例。
若3∶m=n∶7,则m和n成反比例;若=(a,b≠0),则a和b成为正比例。
【点睛】根据正比例意义以及辨识,反比例意义以及辨识进行解答。
12.25
【分析】根据题意,甲、乙两人的速度比是8∶5,把甲的速度看作是“8”,乙的速度看作是“5”,根据乙从A地到B地用了40分钟,由于距离不变,速度和时间成反比例,甲行驶的路程=乙行驶的路程;设甲行这段路需要x分钟,列比例:8x=5×40,解比例,即可求出甲行这段路需要的时间。
【详解】解:设甲行这段路需要x分钟。
8x=5×40
8x=200
x=200÷8
x=25
甲、乙两人的速度比是8∶5,已知乙从A地到B地用了40分钟,那么甲行这段路需要用25分钟。
【点睛】熟练掌握反比例的意义和辨识是解答本题的关键。
13.×
【分析】根据反比例的意义:两个相关联的量,一个量变化,另一个量也随着变化,如果相对应的两个量x和y的乘积一定,即xy=k(定值),那么这两个量叫做成反比例的量,它们的关系叫做反比例关系;解答即可。
【详解】男生人数+女生人数=全班人数(和一定),不符合反比例意义,原题说法错误。
故答案为:×
【点睛】本题主要考查反比例的意义,解题时要明确:只有乘积一定的两种相关联的两种量,才成反比例。
14.×
【分析】由A∶10=B,可得出=10,符合正比例关系式:=k(一定),由此即可判断。
【详解】由A∶10=B,得出A∶B=10,所以A与B成正比例。
故答案为:×
【点睛】此题主要考查正比例与反比例的意义。
15.×
【分析】判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为和成反比例,所以(一定),则,因为,和成反比例,所以(一定),
把,代入式子(一定),
得出:(一定),是和对应的比值一定,所以和成正比例;
故答案为:×
【点睛】本题主要考查对于正、反比例的辨识。
16.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为运动员平均速度所用时间米(一定),符合反比例的意义,所以在400米赛跑中,运动员平均速度和所用时间成反比例。
故答案为:。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
17.√
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】直条所表示的数量直条的长度单位直条表示的数量(一定),也就是比值一定,直条的长度与直条所表示的数量成正比例。
故答案为:√
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
18.x=;x=7.8;x=3.6;x=1
【分析】根据等式的性质,方程两边同时除以计算即可;
根据比例的性质,将原来的式子转换成x=18%×6.5,根据等式的性质,方程两边同时除以计算即可;
根据等式的性质,方程两边同时乘,再同时减去3,最后同时除以计算即可;
根据等式的性质,方程两边同时减去x,再同时减去2,最后同时除以3计算即可。
【详解】x-x=
解:x=
x÷=÷
x=
18%∶=
解:x=18%×6.5
x=1.17
x÷=1.17÷
x=7.8
(x+3)÷=19.5
解:(x+3)÷×=19.5×
x+3=3.9
x+3-3=3.9-3
x=0.9
x÷=0.9÷
x=3.6
2(x+1)=1-(x-4)
解:2x+2=1-x+4
2x+2=5-x
2x+2+x=5-x+x
3x+2=5
3x+2-2=5-2
3x=3
3x÷3=3÷3
x=1
19.(1)见详解
(2)见详解
(3)成正比例,利用见详解
(4)42千克
【分析】(1)利用天数乘每天白白流掉的水的质量即可;
(2)根据统计表中的数据,绘制成统计图;
(3)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
(4)用每天流掉的水的质量×3.5天,即可解答。
【详解】(1)2×12=24(千克)
3×12=36(千克)
4×12=48(千克)
5×12=60(千克)
6×12=72(千克)
天数/天 1 2 3 4 5 6 …
流掉的水量/千克 12 24 36 48 60 72 …
(2)图如下:
(3)1÷12=2÷24=3÷36=4÷48=5÷60=6÷72=(一定),水龙头流水的天数和流掉的水量成正比例。
(4)12×3.5=42(千克)
答:3.5天大约流掉42千克的水。
【点睛】解答本题先根据问题从图中找出所需的信息。然后根据数量关系式“天数×每天的流水量=总流水量”即可作出解答。
20.108转
【分析】一对互相咬合的齿轮,说明在旋转过程中,主动轮与从动轮旋转的齿数相等,齿轮的齿数与每分钟旋转的圈数成反比例,设主动轮每分钟转x转;列比例:25x=45×60,解比例,即可解答。
【详解】解:设主动轮每分钟转x转。
25x=45×60
25x=2700
x=2700÷25
x=108
答:主动轮每分钟转108转。
【点睛】解答本题先判断齿轮的齿数与每分钟转的圈数是成什么比例,再列比例进行解答。
21.15行
【分析】第一种方法:原来每行人数×正好站成的行数=做操总人数,做操总人数÷现在每行站的人数=现在可以占的行数;
第二种方法:设可以站x行,总人数=每行站的人数×站成的行数;由于总人数不变,每行站的人数和行数成反比例。现在每行站的人数×现在可以站的行数=原来每行站的人数×正好站成的行数,列方程:24x=20×18,解方程,即可解答。
【详解】第一种:20×18÷24
=360÷24
=15(行)
第二种:解:设可以站x行。
24x=20×18
24x=360
24x÷24=360÷24
x=15
答:可以站15行。
【点睛】解答本题的关键明确总人数不变,利用总人数不变,进行解答。
22.96块
【分析】根据题意可知,会议室的面积是不变的,每一块方砖的面积与所需块数的乘积是一定的,即两种量成反比例;设如果改用边长是5分米的方砖要用x块,列比例:5×5×x=16×150,解比例,即可解答。
【详解】解:设如果改用边长是5分米的方砖要用x块。
5×5×x=16×150
25x=2400
x=2400÷25
x=96
答:如果改用边长是5分米的方砖要用96块。
【点睛】此题首先利用正、反比例的意义判定两种量的关系,解答时关键不要把边长当作面积进行计算。
23.12米
【分析】由于1÷0.5=2,1.4÷0.7=2,1.6÷0.8=2,由此即可知道同一时刻物高与影长成正比,可以设旗杆的实际高度是x米,当竹竿长是1米,影长0.5米时,即旗杆的高度∶旗杆的影长=1∶0.5,据此列出方程,求出未知数的值即可。
【详解】解:设旗杆的实际高度是米,
0.5x=6÷0.5
答:旗杆的实际高度是12米。
【点睛】找出等量关系,是解答此题的关键。
24.(1)成反比例。
(2)18小时
【分析】(1)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,由于72×2=48×3=4×36=6×24=144(万只),可知乘积一定,即生产总数量一定,所以每时生产口罩的数量与时间成反比例。
(2)用总共生产的数量除以每时生产的等于一共需要的时间,把数代入即可求解。
【详解】(1)72×2=48×3=36×4=24×6=144(万只)
答:因为每时生产口罩的数量与时间的积一定,所以每时生产口罩的数量与时间成反比例。
(2)144÷8=18(时)
答:完成这项任务一共需要18小时。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
