4.3角 复习课件(共24张PPT) 人教版数学七年级上册
文档属性
| 名称 | 4.3角 复习课件(共24张PPT) 人教版数学七年级上册 |  | |
| 格式 | zip | ||
| 文件大小 | 294.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 10:50:13 | ||
图片预览




文档简介
(共24张PPT)
第四章复习——角
要点一
1.角的定义一:
有公共端点的两条射线组成的图形
叫做角,这个公共端点叫做角的顶点,这
两条射线叫做角的边.
2.角的定义二:
角可以看成是一条射线绕着它的
端点从一个位置旋转到另一个位置所形成
的图形.射线旋转时经过的平面部分叫角
的内部.
3.角的四种表示方法
表示方法
注意事项
1.用三个大写的字母表示
表示顶点的字母要写在中间
2.用一个顶点的字母来表示
一个字母只表示一个角
3.用一个数字
在靠近顶点的处画上弧线,
并写上数字
4.希腊字母表示
在靠近顶点的处画上弧线,
并写上希腊字母
4.平角、周角的概念
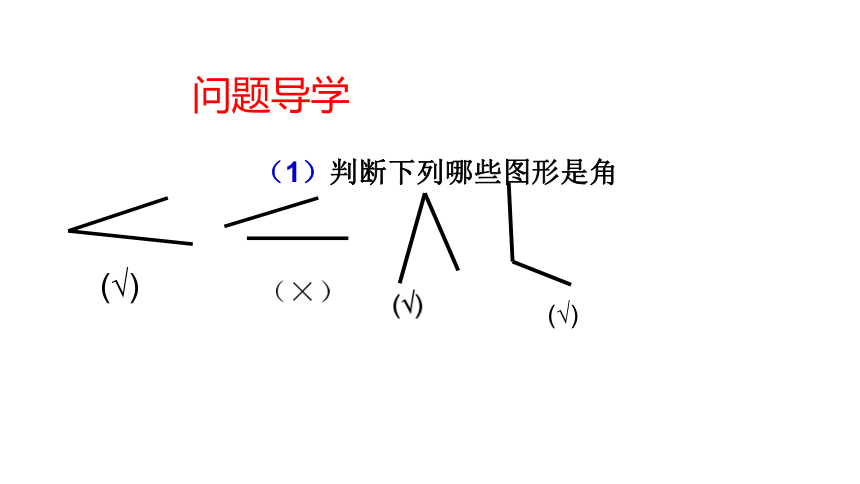
(1)判断下列哪些图形是角
问题导学
(√)
(×)
(√)
(√)
导入新课
复习引入
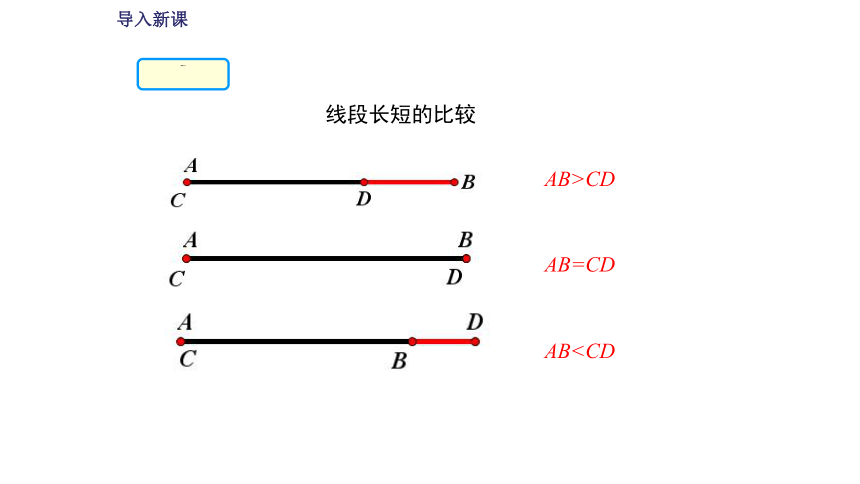
线段长短的比较
AB>CD
ABAB=CD
讲授新课
角的比较
一
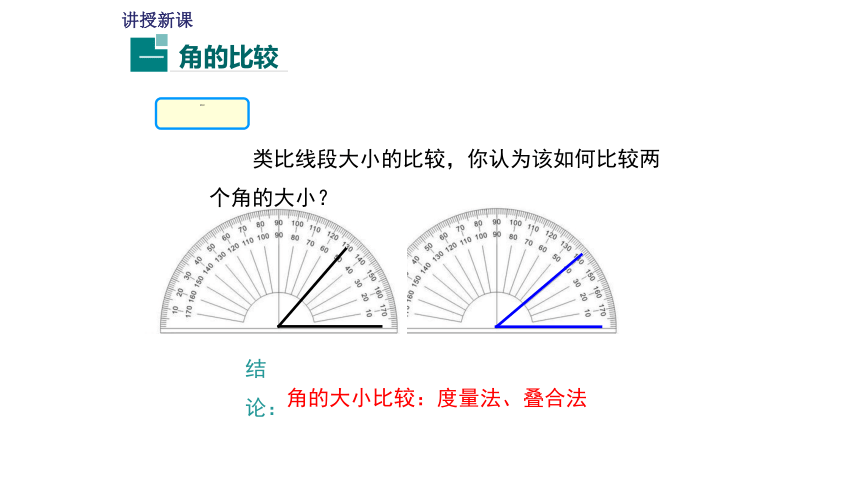
类比线段大小的比较,你认为该如何比较两个角的大小?
合作探究
结论:
角的大小比较:度量法、叠合法
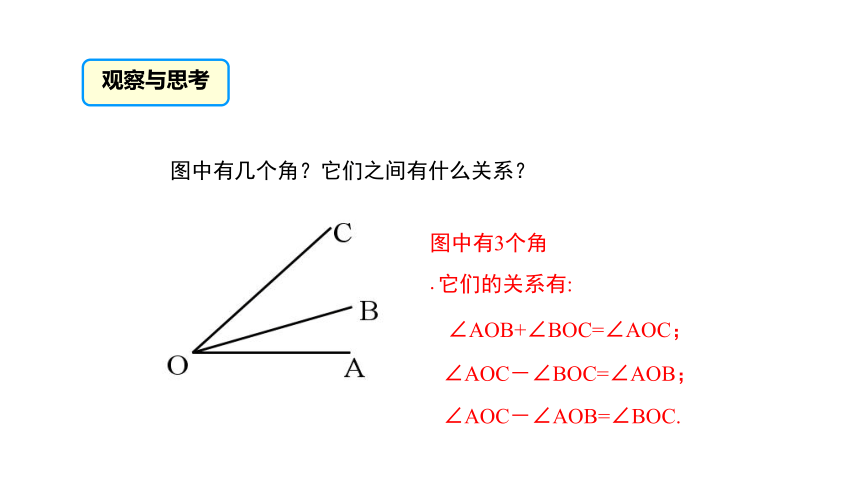
图中有几个角?它们之间有什么关系?
图中有3个角.
它们的关系有:
∠AOB+∠BOC=∠AOC;
∠AOC-∠BOC=∠AOB;
∠AOC-∠AOB=∠BOC.
观察与思考
1
O
A
B
2
C
B
O
顶点与一边重合
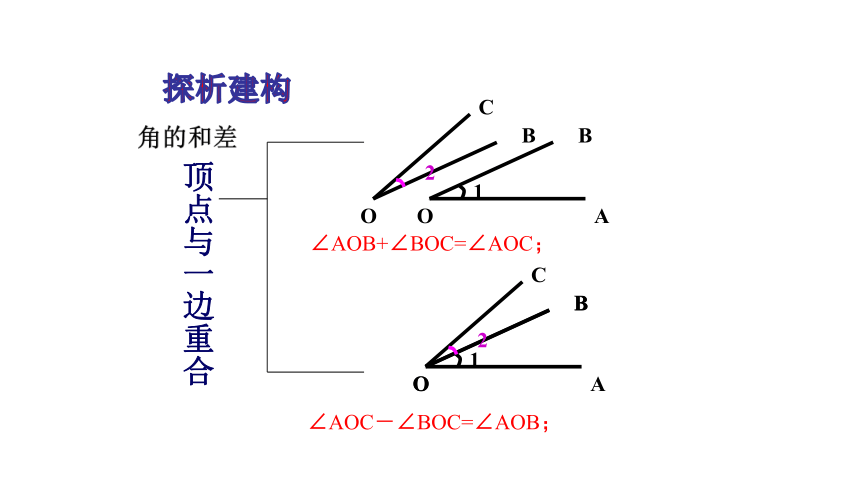
角的和差
探析建构
∠AOB+∠BOC=∠AOC;
1
O
A
B
2
C
B
O
∠AOC-∠BOC=∠AOB;
探析建构
如果∠AOC=60°∠AOB=20°
求∠BOC
解:因为∠AOB+∠BOC=∠AOC;
所以∠AOC-∠AOB=∠BOC.
∠BOC=60°-20°=40°
3.集体探究
我来当老师…
例2 如图,OB是∠ AOC的平分线,OD是∠COE的平分线.
(1)如果∠ AOC=80°,那么∠BOC是多少度?
解:因为OB平分∠ AOC,∠ AOC=80°
所以∠AOB=1/2∠AOC=80°/2=40°
所以∠BOC=∠AOB=40°
探析建构
例1 如图:O是直线AB上一点,∠AOC=53°17′
求∠BOC的度数
B
A
O
C
解:因为∠AOB是平角
∠AOB=∠AOC+∠BOC
所以∠BOC=∠AOB-∠AOC
=180°-53°17′
=126°43′
类比线段的中点,射线OB有没有一种特殊的位置,
若有,此时三个角之间有怎样的关系
B
B
B
B
角的平分线
二
观察思考
∵OC是∠AOB的角平分线,
∴∠AOC =∠BOC =1/2∠AOB
∠AOB =2∠BOC =2∠AOC
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线
应用格式:
O
B
A
C
例2 如图,OB是∠ AOC的平分线,OD是∠COE的平分线.
(2)如果∠ AOB=40°, ∠ DOE=30°那么∠BOD是多少度?
解:因为OB平分∠ AOC,
所以∠BOC=∠AOB=40°
因为OD平分∠ COE,
所以∠COD=∠DOE=30°
所以∠BOD=∠BOC+∠COD=40°+30°=70°
拓展提升
2
1
讲授新课
余角和补角的概念
一
如果两个角的和等于90°(直角),就说这两个角互为余角(简称互余).
定义:
如图,可以说∠1是∠2的余角或∠2是∠1的余角.
3
4
如果两个角的和等于180°(平角),就说这两个角互为补角(简称互补).
定义:
如图,可以说∠3是∠4的余角或∠4是∠3的补角.
典例精析
例1. 若一个角的补角等于它的余角的4 倍,求这个角的度数.
解:设这个角是x°,则它的补角是(180°-x°),余角是(90°-x°) .
根据题意,得
180°-x°= 4 (90°-x°)
解得
x=60
答:这个角的度数是60 °.
∠1与∠2,∠3都互为补角,
∠2与∠3的大小有什么关系?
余角和补角的性质
二
思考:
1
2
同角(等角)的补角相等
结论:
3
∠2=180°-∠1
∠3=180°-∠1
同角(等角)的余角相等
类似的可以得到:
例2 如图,点A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和∠BOC,图中哪些角互为余角?
解:因为点A,O,B在同一直线上,所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC和∠BOC,所以∠COD+∠COE=1/2∠AOC+1/2∠BOC
=1/2(∠AOC+∠BOC)=90°.
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠AOD和∠BOE也互为余角.
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:_________
东南方向:_________
东北方向:_________
射线 OA
A
B
C
D
OB
OC
OD
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
方位角
三
八大方位
东西方向的海岸线上有A、B两个观测站,分别观测到渔船C的位置如图所示,则渔船C在观测站A的 偏 °,渔船C在观测站B的 偏 °.你能说出观测站A在渔船C的什么方向吗?观测站B呢?
例4 如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上.同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位
的方法画出表示客轮B,货
轮C和海岛D方向的射线.
O
●
东
南
西
北
● A
60°
● B
● D
C ●
40°
10°
45°
度量法、叠合法
1.比较两个角大小的方法
2.角的和、差关系
3.角平分线
从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线
课堂小结
互余 互补
两角间的数量关系
对应图形
性质
同角或等角的
余角相等
同角或等角的
补角相等
课堂小结
第四章复习——角
要点一
1.角的定义一:
有公共端点的两条射线组成的图形
叫做角,这个公共端点叫做角的顶点,这
两条射线叫做角的边.
2.角的定义二:
角可以看成是一条射线绕着它的
端点从一个位置旋转到另一个位置所形成
的图形.射线旋转时经过的平面部分叫角
的内部.
3.角的四种表示方法
表示方法
注意事项
1.用三个大写的字母表示
表示顶点的字母要写在中间
2.用一个顶点的字母来表示
一个字母只表示一个角
3.用一个数字
在靠近顶点的处画上弧线,
并写上数字
4.希腊字母表示
在靠近顶点的处画上弧线,
并写上希腊字母
4.平角、周角的概念
(1)判断下列哪些图形是角
问题导学
(√)
(×)
(√)
(√)
导入新课
复习引入
线段长短的比较
AB>CD
AB
讲授新课
角的比较
一
类比线段大小的比较,你认为该如何比较两个角的大小?
合作探究
结论:
角的大小比较:度量法、叠合法
图中有几个角?它们之间有什么关系?
图中有3个角.
它们的关系有:
∠AOB+∠BOC=∠AOC;
∠AOC-∠BOC=∠AOB;
∠AOC-∠AOB=∠BOC.
观察与思考
1
O
A
B
2
C
B
O
顶点与一边重合
角的和差
探析建构
∠AOB+∠BOC=∠AOC;
1
O
A
B
2
C
B
O
∠AOC-∠BOC=∠AOB;
探析建构
如果∠AOC=60°∠AOB=20°
求∠BOC
解:因为∠AOB+∠BOC=∠AOC;
所以∠AOC-∠AOB=∠BOC.
∠BOC=60°-20°=40°
3.集体探究
我来当老师…
例2 如图,OB是∠ AOC的平分线,OD是∠COE的平分线.
(1)如果∠ AOC=80°,那么∠BOC是多少度?
解:因为OB平分∠ AOC,∠ AOC=80°
所以∠AOB=1/2∠AOC=80°/2=40°
所以∠BOC=∠AOB=40°
探析建构
例1 如图:O是直线AB上一点,∠AOC=53°17′
求∠BOC的度数
B
A
O
C
解:因为∠AOB是平角
∠AOB=∠AOC+∠BOC
所以∠BOC=∠AOB-∠AOC
=180°-53°17′
=126°43′
类比线段的中点,射线OB有没有一种特殊的位置,
若有,此时三个角之间有怎样的关系
B
B
B
B
角的平分线
二
观察思考
∵OC是∠AOB的角平分线,
∴∠AOC =∠BOC =1/2∠AOB
∠AOB =2∠BOC =2∠AOC
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线
应用格式:
O
B
A
C
例2 如图,OB是∠ AOC的平分线,OD是∠COE的平分线.
(2)如果∠ AOB=40°, ∠ DOE=30°那么∠BOD是多少度?
解:因为OB平分∠ AOC,
所以∠BOC=∠AOB=40°
因为OD平分∠ COE,
所以∠COD=∠DOE=30°
所以∠BOD=∠BOC+∠COD=40°+30°=70°
拓展提升
2
1
讲授新课
余角和补角的概念
一
如果两个角的和等于90°(直角),就说这两个角互为余角(简称互余).
定义:
如图,可以说∠1是∠2的余角或∠2是∠1的余角.
3
4
如果两个角的和等于180°(平角),就说这两个角互为补角(简称互补).
定义:
如图,可以说∠3是∠4的余角或∠4是∠3的补角.
典例精析
例1. 若一个角的补角等于它的余角的4 倍,求这个角的度数.
解:设这个角是x°,则它的补角是(180°-x°),余角是(90°-x°) .
根据题意,得
180°-x°= 4 (90°-x°)
解得
x=60
答:这个角的度数是60 °.
∠1与∠2,∠3都互为补角,
∠2与∠3的大小有什么关系?
余角和补角的性质
二
思考:
1
2
同角(等角)的补角相等
结论:
3
∠2=180°-∠1
∠3=180°-∠1
同角(等角)的余角相等
类似的可以得到:
例2 如图,点A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和∠BOC,图中哪些角互为余角?
解:因为点A,O,B在同一直线上,所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC和∠BOC,所以∠COD+∠COE=1/2∠AOC+1/2∠BOC
=1/2(∠AOC+∠BOC)=90°.
所以∠COD和∠COE互为余角,
同理∠AOD和∠BOE,∠AOD和∠COE,∠AOD和∠BOE也互为余角.
东
西
北
南
O
(1)正东,正南,正西,正北
(2)西北方向:_________
西南方向:_________
东南方向:_________
东北方向:_________
射线 OA
A
B
C
D
OB
OC
OD
45°
射线OE
射线OF
射线OG
射线OH
E
G
F
H
45°
45°
45°
方位角
三
八大方位
东西方向的海岸线上有A、B两个观测站,分别观测到渔船C的位置如图所示,则渔船C在观测站A的 偏 °,渔船C在观测站B的 偏 °.你能说出观测站A在渔船C的什么方向吗?观测站B呢?
例4 如图,货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上.同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位
的方法画出表示客轮B,货
轮C和海岛D方向的射线.
O
●
东
南
西
北
● A
60°
● B
● D
C ●
40°
10°
45°
度量法、叠合法
1.比较两个角大小的方法
2.角的和、差关系
3.角平分线
从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线
课堂小结
互余 互补
两角间的数量关系
对应图形
性质
同角或等角的
余角相等
同角或等角的
补角相等
课堂小结
