第七章:平面直角坐标系练习题(含解析)2021-2022学年吉林省各地七年级下学期人教版数学期末试题选编
文档属性
| 名称 | 第七章:平面直角坐标系练习题(含解析)2021-2022学年吉林省各地七年级下学期人教版数学期末试题选编 |
|
|
| 格式 | zip | ||
| 文件大小 | 634.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 00:00:00 | ||
图片预览




文档简介
第七章:平面直角坐标系
一、单选题
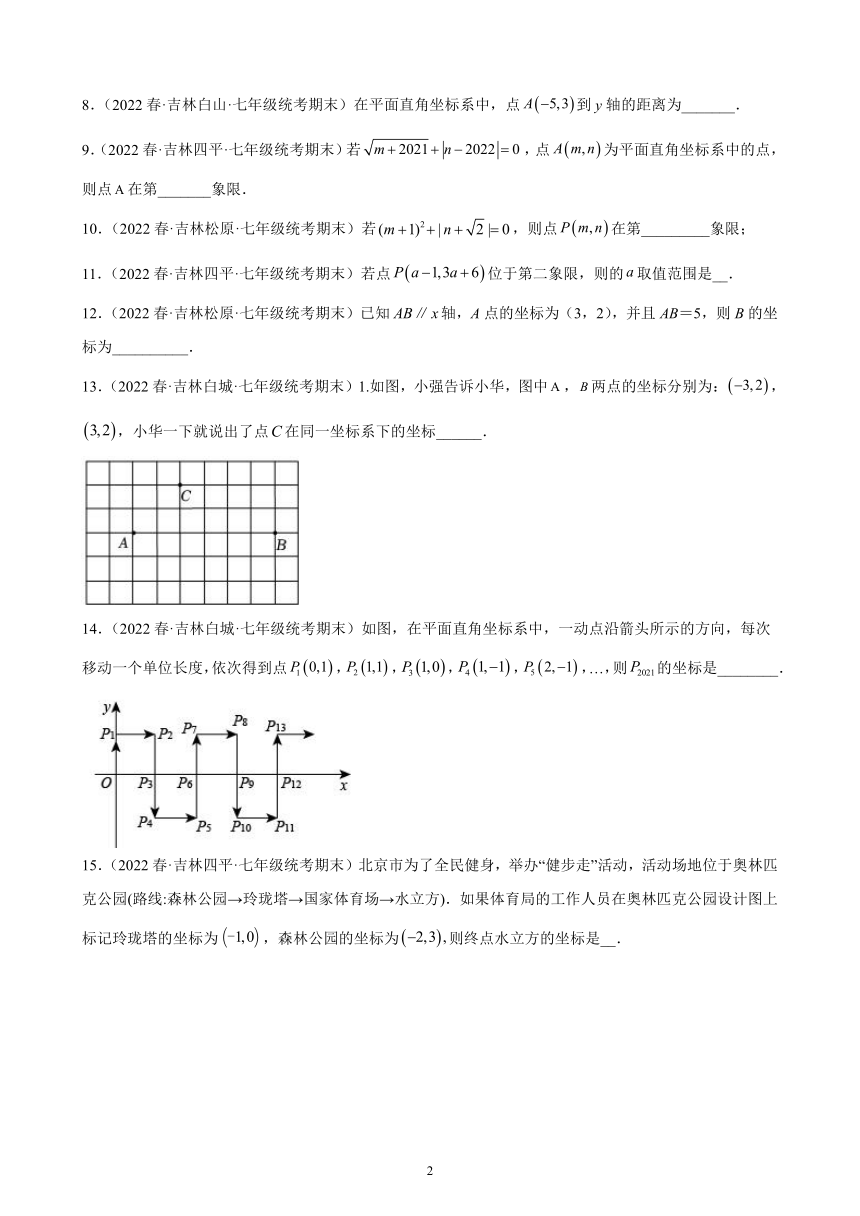
1.(2022春·吉林延边·七年级统考期末)象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )
A.(2,3) B.(1,3) C.(1,2) D.(2,3)
2.(2022春·吉林松原·七年级统考期末)若点P是第二象限内的点,且点P到x轴的距离是2,到y轴的距离是3,则点P的坐标是 ( )
A.(2,3) B.(2,-3) C.(-3,2) D.(3,-2)
3.(2022春·吉林四平·七年级统考期末)已知到轴的距离是( )
A. B. C. D.
4.(2022春·吉林四平·七年级统考期末)在平面直角坐标系中,位于第二象限的点的坐标可能是( )
A. B. C. D.
5.(2022春·吉林通化·七年级统考期末)点,在( )象限
A.第一 B.第二 C.第三 D.第四
6.(2022春·吉林白城·七年级统考期末)如果点P(5,y)在第四象限,则y的取值范围是( )
A.y<0 B.y>0 C.y≤0 D.y≥0
二、填空题
7.(2022春·吉林白城·七年级统考期末)已知点,过点A向y轴作垂线,垂足为M,则点M的坐标为________.
8.(2022春·吉林白山·七年级统考期末)在平面直角坐标系中,点到y轴的距离为_______.
9.(2022春·吉林四平·七年级统考期末)若,点为平面直角坐标系中的点,则点在第_______象限.
10.(2022春·吉林松原·七年级统考期末)若,则点在第_________象限;
11.(2022春·吉林四平·七年级统考期末)若点位于第二象限,则的取值范围是__.
12.(2022春·吉林松原·七年级统考期末)已知轴,A点的坐标为(3,2),并且AB=5,则B的坐标为__________.
13.(2022春·吉林白城·七年级统考期末)1.如图,小强告诉小华,图中,两点的坐标分别为:,,小华一下就说出了点在同一坐标系下的坐标______.
14.(2022春·吉林白城·七年级统考期末)如图,在平面直角坐标系中,一动点沿箭头所示的方向,每次移动一个单位长度,依次得到点,,,,,…,则的坐标是________.
15.(2022春·吉林四平·七年级统考期末)北京市为了全民健身,举办“健步走”活动,活动场地位于奥林匹克公园(路线:森林公园→玲珑塔→国家体育场→水立方).如果体育局的工作人员在奥林匹克公园设计图上标记玲珑塔的坐标为,森林公园的坐标为则终点水立方的坐标是__.
16.(2022春·吉林四平·七年级统考期末)如图,在平面直角坐标系中,将线段AB平移至线段CD的位置,连接.若点的对应点为,则点的对应点C的坐标是____________.
17.(2022春·吉林白城·七年级统考期末)将点B (-3, 2)先向右平移m个单位长度,再向上平移n个单位后得到点B.(-1,5),则mn的值为___________________
三、解答题
18.(2022春·吉林松原·七年级统考期末)已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P到x轴、y轴的距离相等.
19.(2022春·吉林四平·七年级统考期末)在平面直角坐标系中,已知点,点P在过点,且与x轴平行的直线上,求出点P的坐标.
20.(2022春·吉林延边·七年级统考期末)如图所示的方格纸中每个小正方形都是边长为1个单位长度的小正方形,在平面直角坐标系中,已知A(1,0),B(4,0),C(3,3),D(1,4).
(1)描出A、B、C、D四点的位置,并顺次连接ABCD;
(2)四边形的面积是 ;
(3)把四边形向左平移5个单位,再向下平移1个单位得到四边形A1B1C1D1,画出平移后的四边形A1B1C1D1,并写出A1、C1的坐标.
21.(2022春·吉林白城·七年级统考期末)如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a, 0),点C的坐标为(0,b),且a、b满足+|b- 12|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O→A→B→C→O的路线移动.
(1)点B的坐标为________;当点 P移动5秒时,点P的坐标为
(2)在移动过程中,当点P移动11秒时,求△OPB的面积.
(3)在(2)的条件下,坐标轴上是否存在点Q,使△OPQ与△OPB的面积相等.若存在,直接写出点Q的坐标;若不存在,请说明理由.
22.(2022春·吉林延边·七年级统考期末)如图,四边形OABC为长方形,以O为坐标原点,OC所在直线为x轴建立平面直角坐标系.已知点A的坐标为(0,5),点C的坐标为(9,0).
(1)直接写出点B的坐标为 ;
(2)有一动点D从原点O出发,以1个单位长度/秒的速度沿线段OA向终点A运动,当直线CD将长方形的周长分为3:4两部分时,求D点的运动时间t值;
(3)在(2)的条件下,点E为坐标轴上一点,若三角形CDE的面积为18,直接写出点E的坐标.
23.(2022春·吉林白山·七年级统考期末)如图在平面直角坐标系中(单位长度为),已知点,,且.
(1)求m,n的值;
(2)若点E是第一象限内的一点,且轴,点E到x轴的距高为4,过点E作x轴的平行线a,与y轴交于点A,点P从点E处出发,以每秒的速度沿直线a向左运动,点Q从原点O同时出发,以每秒的速度沿x轴向右运动,设点Q的运动时间为t秒,请解答下列问题:
①t为何值时,?
②若某一时刻以A,O,Q,P为顶点的四边形的面积是,请直接写出此时t的值.
24.(2022春·吉林松原·七年级统考期末)如图1,在平面直角坐标系中,点A,B的坐标分别为A(m,0),B(n,0)且m、n满足|m+2|+=0,现同时将点A,B分别向上平移3个单位,再向右平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标;
(2)求四边形OBDC的面积;
(3)如图2,点P是线段BD上的一个动点,连接PC、PO,当点P在线段BD上移动时(不与B,D重合)的值是否发生变化,并说明理由.
25.(2022春·吉林通化·七年级统考期末)平面直角坐标系上有一点,请根据题意回答下列问题:
(1)若点在轴上,求出点的坐标.
(2)点的坐标为且轴,求出点P的坐标.
(3)若点到轴的距离为2,直接写出a的值.
26.(2022春·吉林四平·七年级统考期末)1.在平面直角坐标系中,已知:点.
(1)若点在轴上,求出点的坐标;
(2)点________是坐标原点.(填“可能”或“不可能”)
27.(2022春·吉林通化·七年级统考期末)平面直角坐标系中有一点,已知点在第二象限,点到轴的距离为3个单位、到轴距离为4个单位,请回答下列问题:
(1)点的坐标为_________.
(2)若将点向右平移5个单位至,则坐标为_________,若将点向左平移5个单位至,则坐标为_________.
(3)该坐标系内有一点,点与点的横坐标相同,且线段长为3,点坐标为_________.
28.(2022春·吉林白山·七年级统考期末)如图,在平面直角坐标系中,三角形ABC三个顶点的坐标分别为A(-2,1),B(-3,-2),C(1,-2),若先将三角形ABC向上平移3个单位长度,再向右平移2个单位长度,得到三角形,请解答下列问题:
(1)写出点,,的坐标;
(2)在图中画出平移后的三角形;
(3)三角形的面积为 .
29.(2022春·吉林通化·七年级统考期末)如图,平面直角坐标系中有一个的正方形网格,每个小正方形的边长为1个单位长度,每个小正方形的顶点称为格点,点、、均在格点上,请完成下列问题.
(1)点坐标为_________.
(2)将先向_________平移_________个单位、再向_________平移_________个单位到达的位置.
(3)图中阴影部分的面积为_________.
参考答案:
1.B
【分析】根据棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),进而得出原点在帅的位置,进而得出答案.
【详解】解:如图所示:以帅的位置为原点建立平面直角坐标系,
则棋子“炮”的点的坐标为(1,3).
故选:B.
【点睛】本题主要考查了坐标确定位置,根据“馬”和“車”的点的坐标正确确定原点的位置是解题关键.
2.C
【分析】根据第二象限内点的坐标特点及点到坐标轴的距离定义,即可判断出点P的坐标.
【详解】解:点P到x轴的距离是2,则点P的纵坐标为±2,
点P到y轴的距离是3,则点P的横坐标为±3,
由于点P在第二象限,故P坐标为(-3,2),
故选:C.
【点睛】本题考查了各象限内点的坐标的符号特征以及点到坐标轴的距离,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
3.B
【分析】根据点到x轴的距离等于纵坐标的绝对值求解即可.
【详解】到轴的距离是
故答案为:B.
【点睛】本题考查了点到x轴的距离问题,掌握点到x轴的距离等于该点纵坐标的绝对值是解题的关键.
4.C
【分析】根据第二象限的点的横坐标小于0,纵坐标大于0,即可得出正确选项.
【详解】A. 在y轴上,不合题意;
B. 在第四象限,不合题意;
C. 在第二象限,符合题意;
D. 在第三象限,不合题意;
故选C
【点睛】本题主要考查了平面直角坐标系中各象限的点的坐标的符号特点,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
5.A
【分析】平面直角坐标系中各象限的点的特征:第一象限(+,+),第二象限(-,+),第三象限(-,-)第四象限(+,-),分析即可得出答案.
【详解】的横纵坐标均为正数,因此P点在第一象限.
故选A.
【点睛】本题考查了平面直角坐标系中各象限的点的特征,熟练掌握是本题解题的关键.
6.A
【分析】根据点在第四象限的坐标特点解答即可.
【详解】解:∵点P(5,y)在第四象限,
∴y<0.
故选:A.
【点睛】本题考查了平面直角坐标系内各象限点的特点,解答此题的关键是熟记平面直角坐标系中各个象限内点的符号.四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
7.
【分析】根据平面直角坐标系中坐标轴上的点的特点,再结合题意“已知点,过点A向y轴作垂线,垂足为M”,可得点M的横坐标为0,y轴的垂线上的点的纵坐标相同,应为2,综合即可得出点M的坐标.
【详解】解:∵过点A向y轴作垂线,垂足为M,
∴点M在y轴上,
∴点M的横坐标为0,
又∵点,过点A向y轴作垂线,垂足为M,
∴点M的纵坐标为2,
∴点M的坐标为.
故答案为:
【点睛】本题考查了平面直角坐标系中坐标轴上的点的特点,解本题的关键在理解坐标轴上的点的特点.在横坐标上的点,纵坐标为0;在纵坐标上的点,横坐标为0.
8.5
【分析】根据点到y轴的距离是横坐标的绝对值,可得答案.
【详解】解:点A(-5,3)到y轴的距离是:|-5|=5.
故答案为:5.
【点睛】本题考查了点的坐标,正确掌握点的坐标特点是解决的关键.
9.二
【分析】根据非负数的意义可求出m、n的值,再根据点A坐标的特征判定所在的象限.
【详解】解:∵
∴m+2021=0,n-2020=0,
即m=-2021,n=2020,
∴点A(-2021,2020),
∴点A在第二象限.
故答案为:二.
【点睛】本题考查非负数的性质,点的坐标,理解绝对值,算术平方根的性质以及点的坐标的特征是正确解答的关键.
10.三
【分析】先根据绝对值和平方的非负性求出m、n的值,然后判断其所在的象限即可.
【详解】解:∵,,,
∴,,
∴,,
∴,
∴P在第三象限,
故答案为:三.
【点睛】本题主要考查了绝对值和平方的非负性,根据点的坐标判断其所在的象限,解题的关键在于能够准确求出m、n的值.
11.
【分析】根据第二象限的点的特点列出不等式组求解即可.
【详解】∵点位于第二象限
∴
∴
故答案为:.
【点睛】本题考查了解一元一次不等式组的问题,掌握象限的性质、解一元一次不等式组的方法是解题的关键.
12.(-2,2)或(8,2)##(8,2)或(-2,2)
【分析】根据B点位置分类讨论求解.
【详解】解: 轴,
点B的纵坐标与点A的纵坐标相同,都是2;
∵AB=5
∴在直线AB上,过点A向左5个单位得(-2,2),过点A向右5个单位得(8,2).
∴满足条件的点有两个:(-2,2),(8,2).
故答案为:(-2,2)或(8,2).
【点睛】本题主要是对坐标系平行线的性质的直接考查,同时考查了数形结合思想,题目的条件既有数又有形,解决问题的方法也要既依托数也依托形,体现了数形的紧密结合.
13.
【分析】由点A、B的坐标结合平移规律即可得到点C的坐标.
【详解】已知,两点的坐标分别为,,建立如图所示的平面直角坐标系,观察可知,点C的坐标为.
故答案为:.
【点睛】本题考查了坐标确定位置:平面直角坐标系内点与有序实数对一一对应.
14.
【分析】先根据,,即可得到,,再根据,可得,进而得到.
【详解】解:由图可得,,,…,,,,,
,
∴,即,
故答案为:.
【点睛】本题主要考查了点的坐标变化规律,解决问题的关键是根据图形的变化规律得到P6n(2n,0).
15.
【分析】直接利用已知点得出原点位置进而得出答案即可.
【详解】如图所示,终点水立方的坐标是
故答案为:.
【点睛】本题考查了平面直角坐标系的点坐标问题,掌握平面直角坐标系的性质是解题的关键.
16.
【分析】根据点B、D的坐标确定出平移规律,再根据平移规律解答即可.
【详解】解:∵点的对应点为,
∴平移规律为向右平移3个单位,向上平移4个单位,
∴点的对应点C的坐标为.
故答案为: .
【点睛】本题考查了坐标与图形变化-平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
17.6
【分析】由平移的性质得到-3+m=-1,2+n=5,分别解得m,n的值,再代入计算.
【详解】解:由题意得-3+m=-1,2+n=5
解得m=2,n=3
mn=6
故答案为:6.
【点睛】本题考查坐标与平移变换,是基础考点,掌握相关知识是解题关键.
18.(1)P(-6,0);(2)P(-12,-12)或(-4,4)
【分析】(1)利用x轴上点的坐标性质纵坐标为0,进而得出a的值,即可得出答案;
(2)利用点P到x轴、y轴的距离相等,得出横纵坐标相等或互为相反数进而得出答案.
【详解】解:(1)∵点P(a-2,2a+8)在x轴上,
∴2a+8=0,
解得:a=-4,
故a-2=-4-2=-6,
则P(-6,0);
(2)∵点P到x轴、y轴的距离相等,
∴a-2=2a+8或a-2+2a+8=0,
解得:a=-10,或a=-2,
故当a=-10时,a-2=-12,2a+8=-12,
则P(-12,-12);
故当a=-2时,a-2=-4,2a+8=4,
则P(-4,4).
综上所述:P(-12,-12)或(-4,4).
【点睛】此题主要考查了点的坐标特征,用到的知识点为:点到两坐标轴的距离相等,那么点的横纵坐标相等或互为相反数以及点在坐标轴上的点的性质.
19.
【分析】根据点P在与x轴平行的直线上,可得点的纵坐标为 5,即可求得m的值,再代入点P的坐标即可求解.
【详解】解:由题意得,,
解得,
∴,
则点P的坐标为.
【点睛】本题考查了点的坐标,涉及的知识点为:平行于x轴的直线上的点的纵坐标相等,熟练掌握知识点是解题的关键.
20.(1)见解析;(2);(3)见解析,点A1的坐标为(﹣4,﹣1),点C1的坐标为(﹣2,2).
【分析】(1)根据平面直角坐标系和点的坐标,描点顺次连接即可;
(2)根据四边形ABCD的面积=△ACD的面积+△ABC的面积求解即可;
(3)根据平移方式,先确定对应点的坐标,然后描点,顺次连接即可.
【详解】解:(1)在平面直角坐标系中描出A(1,0),B(4,0),C(3,3),D(1,4),然后顺次连结,
如图,四边形ABCD为所作;
(2)四边形ABCD的面积=×4×2+×3×3=;
故答案为:;
(3)如图,四边形A1B1C1D1为所作,点A1的坐标为(﹣4,﹣1),点C1的坐标为(﹣2,2).
【点睛】本题主要考查了坐标与图形,平移作图,四边形面积,解题的关键在于能够熟练掌握相关知识进行求解.
21.(1)(8,12),(8,2);
(2)当点P移动11秒时,△OPB的面积为12;
(3)(0,4)、(0,-4)、(2,0)、(-2,0).
【分析】(1)利用非负数的性质求出a,b,可得B点坐标,再求出点P移动5秒的路程,可得P点坐标;
(2)求出点P的坐标,可得PB=2,然后根据三角形面积公式计算即可;
(3)分情况讨论:①当点Q在y轴上时,②当点Q在x轴上时,分别根据S△OPQ=S△OPB列式求出OQ,即可得到对应的点Q的坐标.
【详解】(1)解:∵,
∴,,
∴,,
∴A(8,0),B(0,12),
∴OA=BC=8,OC=AB=12,
∴B(8,12),
∵点P移动5秒时,移动的路程为5×2=10,
∴P(8,2),
故答案为:(8,12),(8,2);
(2)当点P移动11秒时,移动的路程为:11×2=22,
∴P(6,12),
∴PB=8-6=2,
∴S△OPB=;
(3)分情况讨论:
①当点Q在y轴上时,
∵点P移动11秒时,P点坐标为(6,12),S△OPB=,
∴由S△OPQ=S△OPB 得:,
∴,
∴点Q的坐标为:(0,4)或(0,-4);
②当点Q在x轴上时,
∵点P移动11秒时,P点坐标为(6,12),S△OPB=,
∴由S△OPQ=S△OPB 得:,
∴,
∴点Q的坐标为:(2,0)或(-2,0),
综上,点Q坐标为:(0,4)或(0,-4)或(2,0)或(-2,0).
【点睛】本题考查了算术平方根和绝对值的非负性,坐标与图形,三角形面积计算等知识,熟练掌握数形结合思想与分类讨论思想的应用是解题的关键.
22.(1)(9,5);(2)D点的运动时间为3 秒;(3)点E的坐标为(﹣3,0)或(21,0)或(0,7)或(0,﹣1).
【分析】(1)根据矩形的性质结合A、C的坐标求解即可;
(2)由题意得:OD=t,AD=5﹣t,OC=9,BC=5,AB=9,根据直线CD将长方形OABC的周长分为3:4两部分,得到(OD+OC):(AD+AB+BC)=3:4,即(t+9):(5﹣t+9+5)=3:4,由此求解即可;
(3)分E在x轴和在y轴上两种情况讨论求解即可得到答案
【详解】解:(1)∵四边形OABC为长方形,
而点A的坐标为(0,5),点C的坐标为(9,0),
∴B点坐标为(9,5);
故答案为(9,5);
(2)由题意得:OD=t,AD=5﹣t,OC=9,BC=5,AB=9,
∵直线CD将长方形OABC的周长分为3:4两部分,
∴(OD+OC):(AD+AB+BC)=3:4,
即(t+9):(5﹣t+9+5)=3:4,
∴t=3,
∴D点的运动时间为3 秒;
(3)由(2)得:D点坐标为(0,3),C点坐标为(9,0),
当E在x轴上时,设E点坐标为(a,0),
∵三角形CDE的面积是18,
∴×3×|9﹣a|=18,解得a=-3或a=21,
∴E点坐标为(-3,0)或(21,0).
当E在y轴上时,设E点坐标为(0,a),
∵三角形CDE的面积是18,
∴×9×|3﹣a|=18,解得a=﹣1或a=7,
∴E点坐标为(0,-1)或(0,7).
∴点E的坐标为(﹣3,0)或(21,0)或(0,7)或(0,﹣1).
【点睛】本题主要考查了坐标与图形,三角形面积,解题的关键在于能够熟练掌握相关知识进行求解.
23.(1)
(2)①秒或秒;②或
【分析】(1)根据平方根和绝对值的性质得出方程组,解方程组即可;
(2)①分为当P在AE上时及当P在AE延长线上时两种情况进行讨论,列出关于的方程,解方程即可;
②设秒后四边形的面积为,根据四边形的面积列出关于的方程,进而求出点的坐标.
(1),,,,,即,;
(2)①当P在AE上时,∵AP=OQ,AP=6 2t,OQ=t,∴6-2t=t∴t=2当P在AE延长线上时,∵AP=OQ,AP=2t 6,OQ=t,∴2t 6t=t∴t=6综上所述:当t=2秒或t=6秒时,AP=OQ②设秒后四边形的面积为,当点在轴右侧时,四边形的面积,,解得,,当点在轴左侧时:同理可得,解得,,综上所述,或.
【点睛】本题是四边形综合题,考查了坐标与图形性质,平移的性质,梯形的面积,难度适中.运用数形结合与方程思想是解题的关键.
24.(1)点C(0,3),D(7,3)
(2)18
(3)比值不变,见解析
【分析】(1)根据非负数的性质得到m=-2,n=5,即可求得A(-2,0),B(5,0);根据平移的性质得到点C(0,3),D(7,3);即可得到结果;
(2)根据A,B,C,D的坐标,分别求得OB,CD的长,根据梯形的面积公式进行计算即可求解;
(3)过点P作PE∥CD,根据两直线平行,内错角相等可得∠DCP=∠CPE,根据平行公理可得PE∥AB,再根据两直线平行,内错角相等可得∠BOP=∠OPE,然后求出∠DCP+∠BOP=∠CPE+∠OPE=∠CPO,再求出比值即可;
(1)∵|m+2|+=0,∴m=﹣2,n=5,∴A(﹣2,0),B(5,0),∵点A,B分别向上平移3个单位,再向右平移2个单位,∴点C(0,3),D(7,3)
(2)由(1)可知点C(0,3),D(7,3),B(5,0),∴OB=5,CD=7,OC=3∴S四边形OBDC=(OB+CD)×CO=(5+7)×3=18;
(3),比值不变.理由如下:由平移的性质可得AB∥CD,如图,过点P作PE∥AB,则PE∥CD,∴∠DCP=∠CPE,∠BOP=∠OPE,∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP,∴,比值不变
【点睛】本题考查了坐标与图形,平行线的性质,平移的性质,掌握以上知识是解题的关键.
25.(1)
(2)
(3)或
【分析】(1)在轴上的点纵坐标为0,代入即可求出点的坐标;
(2)平行于y轴的直线,横坐标相同,因此P、Q横坐标相同,代入即可求出点的坐标;
(3)点到轴的距离为2,分类讨论,分为在轴正半轴还是负半轴,因此P点横坐标为2或-2,代入即可算出答案.
(1)∵在轴上,∴,∴,∴,∴.
(2)∵,且轴,∴,∴,∴∴.
(3)∵点到轴的距离为2,∴P点横坐标为2或-2∴或∴或.
【点睛】本题考查了坐标轴上点的特征,平行于坐标轴的直线上的两个点的特征,以点到坐标轴距离等知识,准确掌握知识并进行运用是本题的关键.
26.(1)
(2)不可能
【分析】(1)根据y轴上点的横坐标为0列方程求出m的值,再求解即可;
(2)根据原点的横坐标与纵坐标都为0进行判断即可.
【详解】(1)根据题意,得
.
解得.
则.
.
(2)不可能,理由如下:
当时,
当时,矛盾
所以的横坐标与纵坐标不可能相等,所以点P不可能是坐标原点.
故答案为:不可能.
【点睛】本题考查了各个象限以及坐标轴上点的坐标特点,熟练掌握坐标轴上点的坐标特征是解题的关键.
27.(1)
(2),
(3)或
【分析】(1)根据点到坐标轴的距离可得横纵坐标的绝对值,进而根据第二象限点的坐标特征即可求得点A的坐标;
(2)根据平移方式,向右平移5个将点A的横坐标加5即可得到的坐标,左平移5个单位将点A的横坐标减5即可得到的坐标;
(3)根据题意设,由线段长为3,可得,解绝对值方程即可求解.
(1)
解:∵点到轴的距离为3个单位、到轴距离为4个单位,
设,
∴,
点在第二象限,
,
,
点的坐标为,
故答案为:;
(2)
若将点向右平移5个单位至,则坐标为;
若将点向左平移5个单位至,则坐标为,
故答案为:,;
(3)
根据题意设,线段长为3,
,
解得或,
点坐标为或.
【点睛】本题考查了点到坐标轴的距离,第二象限点的坐标特征,点的平移,平行于坐标轴的线段的长度,理解题意,数形结合是解题的关键.
28.(1)(0,4),(-1,1),(3,1)
(2)见解析
(3)6
【分析】(1)根据坐标的平移规律:横坐标向左平移减,向右平移加;纵坐标向上平移加,向下平移减;解答即可;
(2)根据坐标描点作图即可;
(3)根据坐标计算三角形的底和高,再求面积即可.
【详解】(1)解:点A(-2,1)、B(-3,-2)、C(1,-2)向上平移3个单位长度,再向右平移2个单位长度后,所得坐标为:点(0,4)、(-1,1)、(3,1);
(2)解:如图三角形即为所求;
(3)解:∵三角形的底B1C1=4,高为3,
三角形的面积==6,
故答案是:6.
【点睛】本题考查了坐标平移的规律,坐标的性质;掌握平移的规律是解题关键.
29.(1)(2,3)
(2)右,三,下,二(或下,二,右,三)
(3)9
【分析】(1)根据网格结构,确定点C在平面直角坐标系中的象限,及其到x轴、 y轴的距离分别为,即可得点C的坐标;
(2)根据网格结构,确定A、B、C三点分别同步平移到A1、B1、C1的方向和距离(单位数)即可得到结论;
(3)根据平面直角坐标系中网格结构和平移的性质,可知平行且等于,,根据平行四边形的判定,从而得=,计算即可得到结果.
【详解】(1)解:根据平面直角坐标系及网格结构,可得:
点C在第一象限
到x轴距离为3, y轴的距离为2
∴点C的坐标为(2,3);
(2)解:根据网格结构,
点A平移到A1,需先向,再向下平移2个单位, B、C同步移动;
或先向下平移2个格点,再向右平移3个单位, B、C同步移动.
∴将△ABC先向右平移3个单位、再向下平移2个单位或者先向下平移2个单位、再向右平移3个单位,到达△A1B1C1的位置;
(3)解:根据题意及平移的性质,
,,
∴四边形ABB1A1为平行四边形
∴==3×3=9
【点睛】本题主要考查平面直角坐标系点的坐标特征,作图-平移变换,平面直角坐标系中的图形面积,解题的关键是掌握平移变换的性质及要素(平移方向和平移距离).
一、单选题
1.(2022春·吉林延边·七年级统考期末)象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )
A.(2,3) B.(1,3) C.(1,2) D.(2,3)
2.(2022春·吉林松原·七年级统考期末)若点P是第二象限内的点,且点P到x轴的距离是2,到y轴的距离是3,则点P的坐标是 ( )
A.(2,3) B.(2,-3) C.(-3,2) D.(3,-2)
3.(2022春·吉林四平·七年级统考期末)已知到轴的距离是( )
A. B. C. D.
4.(2022春·吉林四平·七年级统考期末)在平面直角坐标系中,位于第二象限的点的坐标可能是( )
A. B. C. D.
5.(2022春·吉林通化·七年级统考期末)点,在( )象限
A.第一 B.第二 C.第三 D.第四
6.(2022春·吉林白城·七年级统考期末)如果点P(5,y)在第四象限,则y的取值范围是( )
A.y<0 B.y>0 C.y≤0 D.y≥0
二、填空题
7.(2022春·吉林白城·七年级统考期末)已知点,过点A向y轴作垂线,垂足为M,则点M的坐标为________.
8.(2022春·吉林白山·七年级统考期末)在平面直角坐标系中,点到y轴的距离为_______.
9.(2022春·吉林四平·七年级统考期末)若,点为平面直角坐标系中的点,则点在第_______象限.
10.(2022春·吉林松原·七年级统考期末)若,则点在第_________象限;
11.(2022春·吉林四平·七年级统考期末)若点位于第二象限,则的取值范围是__.
12.(2022春·吉林松原·七年级统考期末)已知轴,A点的坐标为(3,2),并且AB=5,则B的坐标为__________.
13.(2022春·吉林白城·七年级统考期末)1.如图,小强告诉小华,图中,两点的坐标分别为:,,小华一下就说出了点在同一坐标系下的坐标______.
14.(2022春·吉林白城·七年级统考期末)如图,在平面直角坐标系中,一动点沿箭头所示的方向,每次移动一个单位长度,依次得到点,,,,,…,则的坐标是________.
15.(2022春·吉林四平·七年级统考期末)北京市为了全民健身,举办“健步走”活动,活动场地位于奥林匹克公园(路线:森林公园→玲珑塔→国家体育场→水立方).如果体育局的工作人员在奥林匹克公园设计图上标记玲珑塔的坐标为,森林公园的坐标为则终点水立方的坐标是__.
16.(2022春·吉林四平·七年级统考期末)如图,在平面直角坐标系中,将线段AB平移至线段CD的位置,连接.若点的对应点为,则点的对应点C的坐标是____________.
17.(2022春·吉林白城·七年级统考期末)将点B (-3, 2)先向右平移m个单位长度,再向上平移n个单位后得到点B.(-1,5),则mn的值为___________________
三、解答题
18.(2022春·吉林松原·七年级统考期末)已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P到x轴、y轴的距离相等.
19.(2022春·吉林四平·七年级统考期末)在平面直角坐标系中,已知点,点P在过点,且与x轴平行的直线上,求出点P的坐标.
20.(2022春·吉林延边·七年级统考期末)如图所示的方格纸中每个小正方形都是边长为1个单位长度的小正方形,在平面直角坐标系中,已知A(1,0),B(4,0),C(3,3),D(1,4).
(1)描出A、B、C、D四点的位置,并顺次连接ABCD;
(2)四边形的面积是 ;
(3)把四边形向左平移5个单位,再向下平移1个单位得到四边形A1B1C1D1,画出平移后的四边形A1B1C1D1,并写出A1、C1的坐标.
21.(2022春·吉林白城·七年级统考期末)如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a, 0),点C的坐标为(0,b),且a、b满足+|b- 12|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O→A→B→C→O的路线移动.
(1)点B的坐标为________;当点 P移动5秒时,点P的坐标为
(2)在移动过程中,当点P移动11秒时,求△OPB的面积.
(3)在(2)的条件下,坐标轴上是否存在点Q,使△OPQ与△OPB的面积相等.若存在,直接写出点Q的坐标;若不存在,请说明理由.
22.(2022春·吉林延边·七年级统考期末)如图,四边形OABC为长方形,以O为坐标原点,OC所在直线为x轴建立平面直角坐标系.已知点A的坐标为(0,5),点C的坐标为(9,0).
(1)直接写出点B的坐标为 ;
(2)有一动点D从原点O出发,以1个单位长度/秒的速度沿线段OA向终点A运动,当直线CD将长方形的周长分为3:4两部分时,求D点的运动时间t值;
(3)在(2)的条件下,点E为坐标轴上一点,若三角形CDE的面积为18,直接写出点E的坐标.
23.(2022春·吉林白山·七年级统考期末)如图在平面直角坐标系中(单位长度为),已知点,,且.
(1)求m,n的值;
(2)若点E是第一象限内的一点,且轴,点E到x轴的距高为4,过点E作x轴的平行线a,与y轴交于点A,点P从点E处出发,以每秒的速度沿直线a向左运动,点Q从原点O同时出发,以每秒的速度沿x轴向右运动,设点Q的运动时间为t秒,请解答下列问题:
①t为何值时,?
②若某一时刻以A,O,Q,P为顶点的四边形的面积是,请直接写出此时t的值.
24.(2022春·吉林松原·七年级统考期末)如图1,在平面直角坐标系中,点A,B的坐标分别为A(m,0),B(n,0)且m、n满足|m+2|+=0,现同时将点A,B分别向上平移3个单位,再向右平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标;
(2)求四边形OBDC的面积;
(3)如图2,点P是线段BD上的一个动点,连接PC、PO,当点P在线段BD上移动时(不与B,D重合)的值是否发生变化,并说明理由.
25.(2022春·吉林通化·七年级统考期末)平面直角坐标系上有一点,请根据题意回答下列问题:
(1)若点在轴上,求出点的坐标.
(2)点的坐标为且轴,求出点P的坐标.
(3)若点到轴的距离为2,直接写出a的值.
26.(2022春·吉林四平·七年级统考期末)1.在平面直角坐标系中,已知:点.
(1)若点在轴上,求出点的坐标;
(2)点________是坐标原点.(填“可能”或“不可能”)
27.(2022春·吉林通化·七年级统考期末)平面直角坐标系中有一点,已知点在第二象限,点到轴的距离为3个单位、到轴距离为4个单位,请回答下列问题:
(1)点的坐标为_________.
(2)若将点向右平移5个单位至,则坐标为_________,若将点向左平移5个单位至,则坐标为_________.
(3)该坐标系内有一点,点与点的横坐标相同,且线段长为3,点坐标为_________.
28.(2022春·吉林白山·七年级统考期末)如图,在平面直角坐标系中,三角形ABC三个顶点的坐标分别为A(-2,1),B(-3,-2),C(1,-2),若先将三角形ABC向上平移3个单位长度,再向右平移2个单位长度,得到三角形,请解答下列问题:
(1)写出点,,的坐标;
(2)在图中画出平移后的三角形;
(3)三角形的面积为 .
29.(2022春·吉林通化·七年级统考期末)如图,平面直角坐标系中有一个的正方形网格,每个小正方形的边长为1个单位长度,每个小正方形的顶点称为格点,点、、均在格点上,请完成下列问题.
(1)点坐标为_________.
(2)将先向_________平移_________个单位、再向_________平移_________个单位到达的位置.
(3)图中阴影部分的面积为_________.
参考答案:
1.B
【分析】根据棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),进而得出原点在帅的位置,进而得出答案.
【详解】解:如图所示:以帅的位置为原点建立平面直角坐标系,
则棋子“炮”的点的坐标为(1,3).
故选:B.
【点睛】本题主要考查了坐标确定位置,根据“馬”和“車”的点的坐标正确确定原点的位置是解题关键.
2.C
【分析】根据第二象限内点的坐标特点及点到坐标轴的距离定义,即可判断出点P的坐标.
【详解】解:点P到x轴的距离是2,则点P的纵坐标为±2,
点P到y轴的距离是3,则点P的横坐标为±3,
由于点P在第二象限,故P坐标为(-3,2),
故选:C.
【点睛】本题考查了各象限内点的坐标的符号特征以及点到坐标轴的距离,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
3.B
【分析】根据点到x轴的距离等于纵坐标的绝对值求解即可.
【详解】到轴的距离是
故答案为:B.
【点睛】本题考查了点到x轴的距离问题,掌握点到x轴的距离等于该点纵坐标的绝对值是解题的关键.
4.C
【分析】根据第二象限的点的横坐标小于0,纵坐标大于0,即可得出正确选项.
【详解】A. 在y轴上,不合题意;
B. 在第四象限,不合题意;
C. 在第二象限,符合题意;
D. 在第三象限,不合题意;
故选C
【点睛】本题主要考查了平面直角坐标系中各象限的点的坐标的符号特点,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
5.A
【分析】平面直角坐标系中各象限的点的特征:第一象限(+,+),第二象限(-,+),第三象限(-,-)第四象限(+,-),分析即可得出答案.
【详解】的横纵坐标均为正数,因此P点在第一象限.
故选A.
【点睛】本题考查了平面直角坐标系中各象限的点的特征,熟练掌握是本题解题的关键.
6.A
【分析】根据点在第四象限的坐标特点解答即可.
【详解】解:∵点P(5,y)在第四象限,
∴y<0.
故选:A.
【点睛】本题考查了平面直角坐标系内各象限点的特点,解答此题的关键是熟记平面直角坐标系中各个象限内点的符号.四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
7.
【分析】根据平面直角坐标系中坐标轴上的点的特点,再结合题意“已知点,过点A向y轴作垂线,垂足为M”,可得点M的横坐标为0,y轴的垂线上的点的纵坐标相同,应为2,综合即可得出点M的坐标.
【详解】解:∵过点A向y轴作垂线,垂足为M,
∴点M在y轴上,
∴点M的横坐标为0,
又∵点,过点A向y轴作垂线,垂足为M,
∴点M的纵坐标为2,
∴点M的坐标为.
故答案为:
【点睛】本题考查了平面直角坐标系中坐标轴上的点的特点,解本题的关键在理解坐标轴上的点的特点.在横坐标上的点,纵坐标为0;在纵坐标上的点,横坐标为0.
8.5
【分析】根据点到y轴的距离是横坐标的绝对值,可得答案.
【详解】解:点A(-5,3)到y轴的距离是:|-5|=5.
故答案为:5.
【点睛】本题考查了点的坐标,正确掌握点的坐标特点是解决的关键.
9.二
【分析】根据非负数的意义可求出m、n的值,再根据点A坐标的特征判定所在的象限.
【详解】解:∵
∴m+2021=0,n-2020=0,
即m=-2021,n=2020,
∴点A(-2021,2020),
∴点A在第二象限.
故答案为:二.
【点睛】本题考查非负数的性质,点的坐标,理解绝对值,算术平方根的性质以及点的坐标的特征是正确解答的关键.
10.三
【分析】先根据绝对值和平方的非负性求出m、n的值,然后判断其所在的象限即可.
【详解】解:∵,,,
∴,,
∴,,
∴,
∴P在第三象限,
故答案为:三.
【点睛】本题主要考查了绝对值和平方的非负性,根据点的坐标判断其所在的象限,解题的关键在于能够准确求出m、n的值.
11.
【分析】根据第二象限的点的特点列出不等式组求解即可.
【详解】∵点位于第二象限
∴
∴
故答案为:.
【点睛】本题考查了解一元一次不等式组的问题,掌握象限的性质、解一元一次不等式组的方法是解题的关键.
12.(-2,2)或(8,2)##(8,2)或(-2,2)
【分析】根据B点位置分类讨论求解.
【详解】解: 轴,
点B的纵坐标与点A的纵坐标相同,都是2;
∵AB=5
∴在直线AB上,过点A向左5个单位得(-2,2),过点A向右5个单位得(8,2).
∴满足条件的点有两个:(-2,2),(8,2).
故答案为:(-2,2)或(8,2).
【点睛】本题主要是对坐标系平行线的性质的直接考查,同时考查了数形结合思想,题目的条件既有数又有形,解决问题的方法也要既依托数也依托形,体现了数形的紧密结合.
13.
【分析】由点A、B的坐标结合平移规律即可得到点C的坐标.
【详解】已知,两点的坐标分别为,,建立如图所示的平面直角坐标系,观察可知,点C的坐标为.
故答案为:.
【点睛】本题考查了坐标确定位置:平面直角坐标系内点与有序实数对一一对应.
14.
【分析】先根据,,即可得到,,再根据,可得,进而得到.
【详解】解:由图可得,,,…,,,,,
,
∴,即,
故答案为:.
【点睛】本题主要考查了点的坐标变化规律,解决问题的关键是根据图形的变化规律得到P6n(2n,0).
15.
【分析】直接利用已知点得出原点位置进而得出答案即可.
【详解】如图所示,终点水立方的坐标是
故答案为:.
【点睛】本题考查了平面直角坐标系的点坐标问题,掌握平面直角坐标系的性质是解题的关键.
16.
【分析】根据点B、D的坐标确定出平移规律,再根据平移规律解答即可.
【详解】解:∵点的对应点为,
∴平移规律为向右平移3个单位,向上平移4个单位,
∴点的对应点C的坐标为.
故答案为: .
【点睛】本题考查了坐标与图形变化-平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
17.6
【分析】由平移的性质得到-3+m=-1,2+n=5,分别解得m,n的值,再代入计算.
【详解】解:由题意得-3+m=-1,2+n=5
解得m=2,n=3
mn=6
故答案为:6.
【点睛】本题考查坐标与平移变换,是基础考点,掌握相关知识是解题关键.
18.(1)P(-6,0);(2)P(-12,-12)或(-4,4)
【分析】(1)利用x轴上点的坐标性质纵坐标为0,进而得出a的值,即可得出答案;
(2)利用点P到x轴、y轴的距离相等,得出横纵坐标相等或互为相反数进而得出答案.
【详解】解:(1)∵点P(a-2,2a+8)在x轴上,
∴2a+8=0,
解得:a=-4,
故a-2=-4-2=-6,
则P(-6,0);
(2)∵点P到x轴、y轴的距离相等,
∴a-2=2a+8或a-2+2a+8=0,
解得:a=-10,或a=-2,
故当a=-10时,a-2=-12,2a+8=-12,
则P(-12,-12);
故当a=-2时,a-2=-4,2a+8=4,
则P(-4,4).
综上所述:P(-12,-12)或(-4,4).
【点睛】此题主要考查了点的坐标特征,用到的知识点为:点到两坐标轴的距离相等,那么点的横纵坐标相等或互为相反数以及点在坐标轴上的点的性质.
19.
【分析】根据点P在与x轴平行的直线上,可得点的纵坐标为 5,即可求得m的值,再代入点P的坐标即可求解.
【详解】解:由题意得,,
解得,
∴,
则点P的坐标为.
【点睛】本题考查了点的坐标,涉及的知识点为:平行于x轴的直线上的点的纵坐标相等,熟练掌握知识点是解题的关键.
20.(1)见解析;(2);(3)见解析,点A1的坐标为(﹣4,﹣1),点C1的坐标为(﹣2,2).
【分析】(1)根据平面直角坐标系和点的坐标,描点顺次连接即可;
(2)根据四边形ABCD的面积=△ACD的面积+△ABC的面积求解即可;
(3)根据平移方式,先确定对应点的坐标,然后描点,顺次连接即可.
【详解】解:(1)在平面直角坐标系中描出A(1,0),B(4,0),C(3,3),D(1,4),然后顺次连结,
如图,四边形ABCD为所作;
(2)四边形ABCD的面积=×4×2+×3×3=;
故答案为:;
(3)如图,四边形A1B1C1D1为所作,点A1的坐标为(﹣4,﹣1),点C1的坐标为(﹣2,2).
【点睛】本题主要考查了坐标与图形,平移作图,四边形面积,解题的关键在于能够熟练掌握相关知识进行求解.
21.(1)(8,12),(8,2);
(2)当点P移动11秒时,△OPB的面积为12;
(3)(0,4)、(0,-4)、(2,0)、(-2,0).
【分析】(1)利用非负数的性质求出a,b,可得B点坐标,再求出点P移动5秒的路程,可得P点坐标;
(2)求出点P的坐标,可得PB=2,然后根据三角形面积公式计算即可;
(3)分情况讨论:①当点Q在y轴上时,②当点Q在x轴上时,分别根据S△OPQ=S△OPB列式求出OQ,即可得到对应的点Q的坐标.
【详解】(1)解:∵,
∴,,
∴,,
∴A(8,0),B(0,12),
∴OA=BC=8,OC=AB=12,
∴B(8,12),
∵点P移动5秒时,移动的路程为5×2=10,
∴P(8,2),
故答案为:(8,12),(8,2);
(2)当点P移动11秒时,移动的路程为:11×2=22,
∴P(6,12),
∴PB=8-6=2,
∴S△OPB=;
(3)分情况讨论:
①当点Q在y轴上时,
∵点P移动11秒时,P点坐标为(6,12),S△OPB=,
∴由S△OPQ=S△OPB 得:,
∴,
∴点Q的坐标为:(0,4)或(0,-4);
②当点Q在x轴上时,
∵点P移动11秒时,P点坐标为(6,12),S△OPB=,
∴由S△OPQ=S△OPB 得:,
∴,
∴点Q的坐标为:(2,0)或(-2,0),
综上,点Q坐标为:(0,4)或(0,-4)或(2,0)或(-2,0).
【点睛】本题考查了算术平方根和绝对值的非负性,坐标与图形,三角形面积计算等知识,熟练掌握数形结合思想与分类讨论思想的应用是解题的关键.
22.(1)(9,5);(2)D点的运动时间为3 秒;(3)点E的坐标为(﹣3,0)或(21,0)或(0,7)或(0,﹣1).
【分析】(1)根据矩形的性质结合A、C的坐标求解即可;
(2)由题意得:OD=t,AD=5﹣t,OC=9,BC=5,AB=9,根据直线CD将长方形OABC的周长分为3:4两部分,得到(OD+OC):(AD+AB+BC)=3:4,即(t+9):(5﹣t+9+5)=3:4,由此求解即可;
(3)分E在x轴和在y轴上两种情况讨论求解即可得到答案
【详解】解:(1)∵四边形OABC为长方形,
而点A的坐标为(0,5),点C的坐标为(9,0),
∴B点坐标为(9,5);
故答案为(9,5);
(2)由题意得:OD=t,AD=5﹣t,OC=9,BC=5,AB=9,
∵直线CD将长方形OABC的周长分为3:4两部分,
∴(OD+OC):(AD+AB+BC)=3:4,
即(t+9):(5﹣t+9+5)=3:4,
∴t=3,
∴D点的运动时间为3 秒;
(3)由(2)得:D点坐标为(0,3),C点坐标为(9,0),
当E在x轴上时,设E点坐标为(a,0),
∵三角形CDE的面积是18,
∴×3×|9﹣a|=18,解得a=-3或a=21,
∴E点坐标为(-3,0)或(21,0).
当E在y轴上时,设E点坐标为(0,a),
∵三角形CDE的面积是18,
∴×9×|3﹣a|=18,解得a=﹣1或a=7,
∴E点坐标为(0,-1)或(0,7).
∴点E的坐标为(﹣3,0)或(21,0)或(0,7)或(0,﹣1).
【点睛】本题主要考查了坐标与图形,三角形面积,解题的关键在于能够熟练掌握相关知识进行求解.
23.(1)
(2)①秒或秒;②或
【分析】(1)根据平方根和绝对值的性质得出方程组,解方程组即可;
(2)①分为当P在AE上时及当P在AE延长线上时两种情况进行讨论,列出关于的方程,解方程即可;
②设秒后四边形的面积为,根据四边形的面积列出关于的方程,进而求出点的坐标.
(1),,,,,即,;
(2)①当P在AE上时,∵AP=OQ,AP=6 2t,OQ=t,∴6-2t=t∴t=2当P在AE延长线上时,∵AP=OQ,AP=2t 6,OQ=t,∴2t 6t=t∴t=6综上所述:当t=2秒或t=6秒时,AP=OQ②设秒后四边形的面积为,当点在轴右侧时,四边形的面积,,解得,,当点在轴左侧时:同理可得,解得,,综上所述,或.
【点睛】本题是四边形综合题,考查了坐标与图形性质,平移的性质,梯形的面积,难度适中.运用数形结合与方程思想是解题的关键.
24.(1)点C(0,3),D(7,3)
(2)18
(3)比值不变,见解析
【分析】(1)根据非负数的性质得到m=-2,n=5,即可求得A(-2,0),B(5,0);根据平移的性质得到点C(0,3),D(7,3);即可得到结果;
(2)根据A,B,C,D的坐标,分别求得OB,CD的长,根据梯形的面积公式进行计算即可求解;
(3)过点P作PE∥CD,根据两直线平行,内错角相等可得∠DCP=∠CPE,根据平行公理可得PE∥AB,再根据两直线平行,内错角相等可得∠BOP=∠OPE,然后求出∠DCP+∠BOP=∠CPE+∠OPE=∠CPO,再求出比值即可;
(1)∵|m+2|+=0,∴m=﹣2,n=5,∴A(﹣2,0),B(5,0),∵点A,B分别向上平移3个单位,再向右平移2个单位,∴点C(0,3),D(7,3)
(2)由(1)可知点C(0,3),D(7,3),B(5,0),∴OB=5,CD=7,OC=3∴S四边形OBDC=(OB+CD)×CO=(5+7)×3=18;
(3),比值不变.理由如下:由平移的性质可得AB∥CD,如图,过点P作PE∥AB,则PE∥CD,∴∠DCP=∠CPE,∠BOP=∠OPE,∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP,∴,比值不变
【点睛】本题考查了坐标与图形,平行线的性质,平移的性质,掌握以上知识是解题的关键.
25.(1)
(2)
(3)或
【分析】(1)在轴上的点纵坐标为0,代入即可求出点的坐标;
(2)平行于y轴的直线,横坐标相同,因此P、Q横坐标相同,代入即可求出点的坐标;
(3)点到轴的距离为2,分类讨论,分为在轴正半轴还是负半轴,因此P点横坐标为2或-2,代入即可算出答案.
(1)∵在轴上,∴,∴,∴,∴.
(2)∵,且轴,∴,∴,∴∴.
(3)∵点到轴的距离为2,∴P点横坐标为2或-2∴或∴或.
【点睛】本题考查了坐标轴上点的特征,平行于坐标轴的直线上的两个点的特征,以点到坐标轴距离等知识,准确掌握知识并进行运用是本题的关键.
26.(1)
(2)不可能
【分析】(1)根据y轴上点的横坐标为0列方程求出m的值,再求解即可;
(2)根据原点的横坐标与纵坐标都为0进行判断即可.
【详解】(1)根据题意,得
.
解得.
则.
.
(2)不可能,理由如下:
当时,
当时,矛盾
所以的横坐标与纵坐标不可能相等,所以点P不可能是坐标原点.
故答案为:不可能.
【点睛】本题考查了各个象限以及坐标轴上点的坐标特点,熟练掌握坐标轴上点的坐标特征是解题的关键.
27.(1)
(2),
(3)或
【分析】(1)根据点到坐标轴的距离可得横纵坐标的绝对值,进而根据第二象限点的坐标特征即可求得点A的坐标;
(2)根据平移方式,向右平移5个将点A的横坐标加5即可得到的坐标,左平移5个单位将点A的横坐标减5即可得到的坐标;
(3)根据题意设,由线段长为3,可得,解绝对值方程即可求解.
(1)
解:∵点到轴的距离为3个单位、到轴距离为4个单位,
设,
∴,
点在第二象限,
,
,
点的坐标为,
故答案为:;
(2)
若将点向右平移5个单位至,则坐标为;
若将点向左平移5个单位至,则坐标为,
故答案为:,;
(3)
根据题意设,线段长为3,
,
解得或,
点坐标为或.
【点睛】本题考查了点到坐标轴的距离,第二象限点的坐标特征,点的平移,平行于坐标轴的线段的长度,理解题意,数形结合是解题的关键.
28.(1)(0,4),(-1,1),(3,1)
(2)见解析
(3)6
【分析】(1)根据坐标的平移规律:横坐标向左平移减,向右平移加;纵坐标向上平移加,向下平移减;解答即可;
(2)根据坐标描点作图即可;
(3)根据坐标计算三角形的底和高,再求面积即可.
【详解】(1)解:点A(-2,1)、B(-3,-2)、C(1,-2)向上平移3个单位长度,再向右平移2个单位长度后,所得坐标为:点(0,4)、(-1,1)、(3,1);
(2)解:如图三角形即为所求;
(3)解:∵三角形的底B1C1=4,高为3,
三角形的面积==6,
故答案是:6.
【点睛】本题考查了坐标平移的规律,坐标的性质;掌握平移的规律是解题关键.
29.(1)(2,3)
(2)右,三,下,二(或下,二,右,三)
(3)9
【分析】(1)根据网格结构,确定点C在平面直角坐标系中的象限,及其到x轴、 y轴的距离分别为,即可得点C的坐标;
(2)根据网格结构,确定A、B、C三点分别同步平移到A1、B1、C1的方向和距离(单位数)即可得到结论;
(3)根据平面直角坐标系中网格结构和平移的性质,可知平行且等于,,根据平行四边形的判定,从而得=,计算即可得到结果.
【详解】(1)解:根据平面直角坐标系及网格结构,可得:
点C在第一象限
到x轴距离为3, y轴的距离为2
∴点C的坐标为(2,3);
(2)解:根据网格结构,
点A平移到A1,需先向,再向下平移2个单位, B、C同步移动;
或先向下平移2个格点,再向右平移3个单位, B、C同步移动.
∴将△ABC先向右平移3个单位、再向下平移2个单位或者先向下平移2个单位、再向右平移3个单位,到达△A1B1C1的位置;
(3)解:根据题意及平移的性质,
,,
∴四边形ABB1A1为平行四边形
∴==3×3=9
【点睛】本题主要考查平面直角坐标系点的坐标特征,作图-平移变换,平面直角坐标系中的图形面积,解题的关键是掌握平移变换的性质及要素(平移方向和平移距离).
