安徽省滁州市定远县青山初级中学2022-2023学年九年级下学期4月质检数学试卷(含解析)
文档属性
| 名称 | 安徽省滁州市定远县青山初级中学2022-2023学年九年级下学期4月质检数学试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 178.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 10:41:09 | ||
图片预览



文档简介
2022-2023学年九年级(下)4月质检试卷
数 学
注意事项:
1.你拿到的试卷满分为150分,考试时间为150分钟;
2.试卷包括“试题卷”和“答题卷”两部分,请务必在“答题卷”上答题,在“试题卷”上答题是无效的;
3.考试结束后,请将“试题卷”和“答题卷”一并交回。
一、选择题(本大题共10小题,每小题4分,共40分。在每小题列出的选项中,选出符合题目的一项)
1. 的绝对值是( )
A. B. C. D.
2. 以反映伟大抗美援朝精神为题材的电影长津湖,作为国庆献礼片,截止到年月底,票房已突破亿,试用科学记数法表示亿为( )
A. B. C. D.
3. 如图,是由个同样大小的正方体摆成的几何体,将正方体移走后,所得几何体( )
A. 主视图不变,左视图改变
B. 主视图不变,左视图不变
C. 主视图改变,左视图不变
D. 主视图改变,左视图改变
4. 下列计算正确的是( )
A. B. C. D.
5. 阳光中学举行学生运动会,小汪和小勇参加了米跑.路程单位:米与时间单位:分钟之间的函数图象如图所示,两位同学在跑步中均保持匀速,则下列说法错误的是( )
A. 小勇的平均速度为米分
B. 到终点前分钟,小汪的速度比小勇的速度快米分
C. 小勇和小汪同时达到终点
D. 小汪和小勇的平均速度相等
6. “宫商角徵羽”是中国古乐的五个基本音阶相当于西乐的,,,,,是采用“三分损益法”通过数学方法获得现有一款“一起听古音”的音乐玩具,音乐小球从处沿轨道进入小洞就可以发出相应的声音,且小球进入每个小洞中可能性大小相同现有一个音乐小球从处先后两次进入小洞,先发出“商”音,再发出“羽”音的概率是( )
A. B. C. D.
7. 如图,在中,,,点,分别在和上,,若以为直径的交的中点,可知的直径是( )
A.
B.
C.
D.
8. 如图,在中,分别以,为圆心,大于长为半径作弧,两弧分别相交于,两点,作直线,分别交线段,于点,,若,的周长为,则的长度为( )
A. B. C. D.
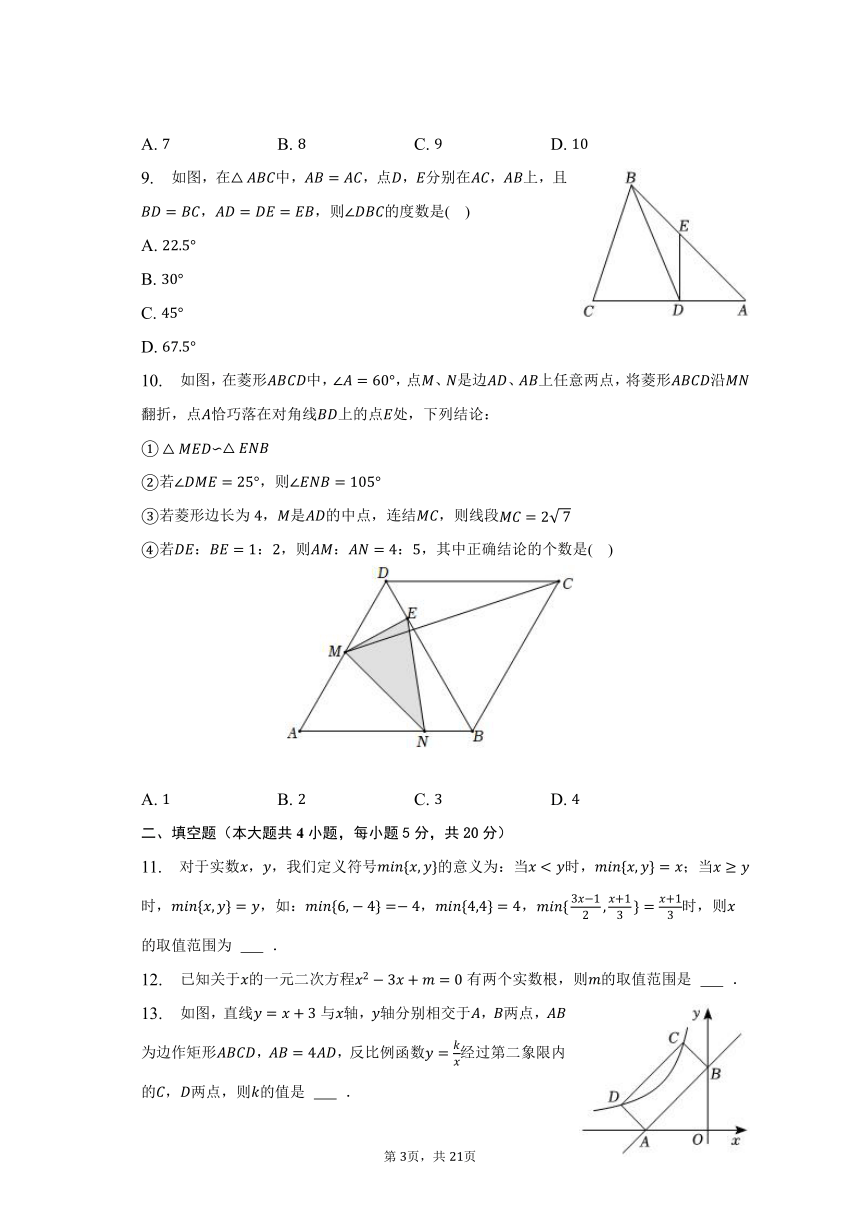
9. 如图,在中,,点,分别在,上,且,,则的度数是( )
A.
B.
C.
D.
10. 如图,在菱形中,,点、是边、上任意两点,将菱形沿翻折,点恰巧落在对角线上的点处,下列结论:
∽
若,则
若菱形边长为,是的中点,连结,则线段
若::,则::,其中正确结论的个数是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
11. 对于实数,,我们定义符号的意义为:当时,;当时,,如:,,时,则的取值范围为 .
12. 已知关于的一元二次方程有两个实数根,则的取值范围是 .
13. 如图,直线与轴,轴分别相交于,两点,为边作矩形,,反比例函数经过第二象限内的,两点,则的值是 .
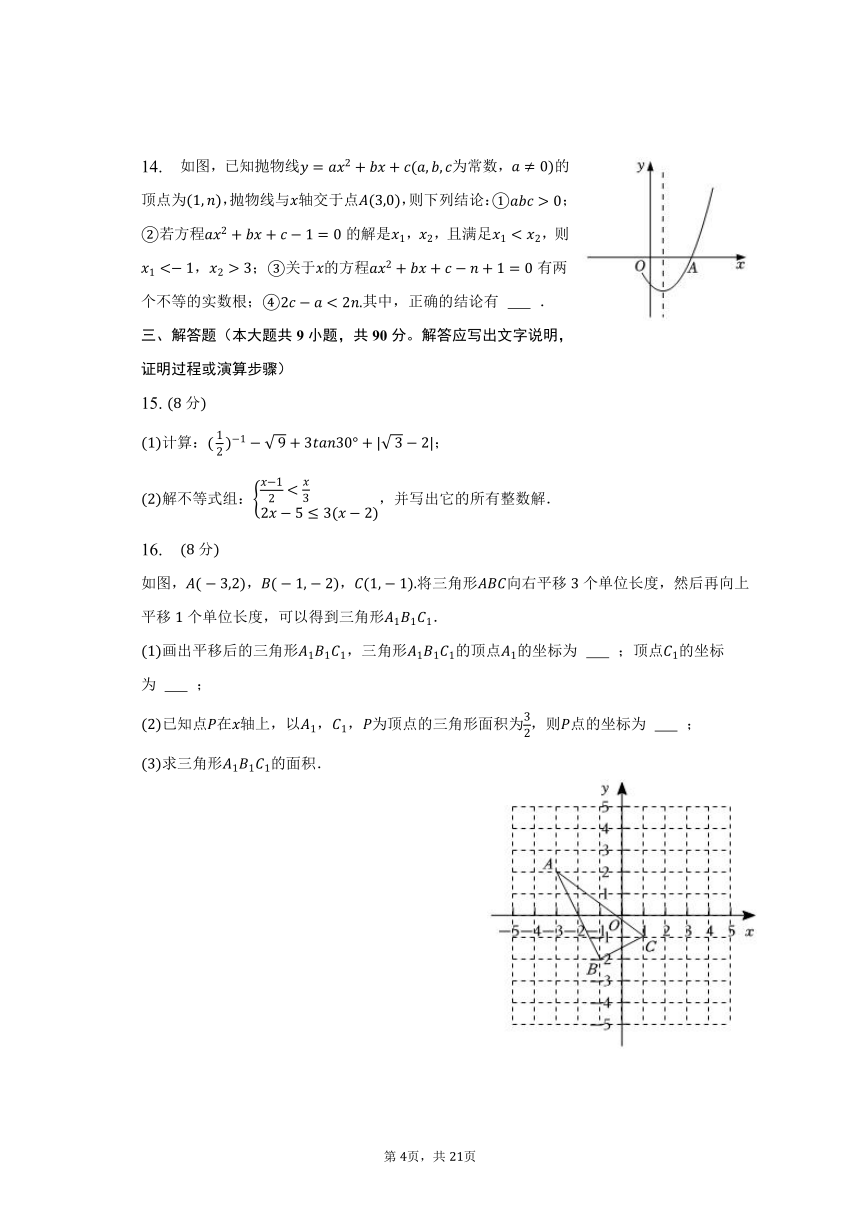
14. 如图,已知抛物线为常数,的顶点为,抛物线与轴交于点,则下列结论:;若方程的解是,,且满足,则,;关于的方程有两个不等的实数根;其中,正确的结论有 .
三、解答题(本大题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤)
15. 分
计算:;
解不等式组:,并写出它的所有整数解.
16. 分
如图,,,将三角形向右平移个单位长度,然后再向上平移个单位长度,可以得到三角形.
画出平移后的三角形,三角形的顶点的坐标为 ;顶点的坐标为 ;
已知点在轴上,以,,为顶点的三角形面积为,则点的坐标为 ;
求三角形的面积.
17. 分
某商场销售甲、乙两种商品,其中甲种商品进价为元件,售价为元件;乙种商品进价为元件,售价为元件现商场用元购进这两种商品并全部售出,两种商品的总利润为元,问该商场购进甲、乙两种商品各多少件?
18. 分
某市采用分段收费的方式按月计算每户家庭的水费,收费标准如表:
户月用水量 收费标准元
不超过
超过,但不超过的部分
超过的部分
小明家月份用水量为,应缴纳水费 元;
设某户某月的用水量为,应缴纳水费多少元?用含的代数式表示
小红家月份和月份的用水量共,且月份用水量比月份多,这两个月共缴纳水费元,则小红家月份和月份的用水量分别为 , .
19. 分
如图,是的外接圆,直径的长为,过点的切线交的延长线于点,连接.
若,求的长;
若,求证:.
20. 分
如图,大楼底部堆放着一堆装修垃圾,在装修垃圾的旁边有一幢别墅,在别墅的顶端处测得装修垃圾边缘点的俯角为,测得大楼顶端的仰角为点,,在同一水平直线上已知,装修垃圾底部,求大楼的高.
21. 分
年月日,“天宫课堂”第三课开讲为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下组满分分,组:,组:,组:,组:,组:,并绘制了如图不完整的统计图请结合统计图,解答下列问题:
频数分布直方图中 ,所抽取学生成绩的中位数落在 组;
补全学生成绩频数分布直方图;
若成绩在分及以上为优秀,学校共有名学生,估计该校成绩优秀的学生有多少人?
22. 分
如图,为四边形的对角线,与关于直线对称,经过的中点,连接,.
求证:;
若,求证:;
如图,在的条件下,连接交于点,若,求的长.
23. 分
已知:如图,二次函数与轴交于点,,点在点左侧,交轴于点,.
求抛物线的解析式;
在第一象限的抛物线上有一点,连接,若,求点坐标;
点在第一象限的抛物线上,于点,求的最大值?
答案和解析
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
【解析】解:根据题意画图如下:
共有种等可能的情况数,其中先发出“商”音,再发出“羽”音的有种,
则先发出“商”音,再发出“羽”音的概率是.
故选:.
画树状图,共有种等可能的结果,其中先发出“商”音,再发出“羽”音的结果有种,再由概率公式求解即可.
本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.掌握概率公式:概率所求情况数与总情况数之比是解题的关键.
7.【答案】
【解析】解:如图,连接,
,是的中点,,
,,,
,
是的直径,
,
,
≌,
,
由勾股定理得:.
故选:.
8.【答案】
【解析】解:由题意得,直线为线段的垂直平分线,
,
的周长为,
.
故答案为:.
由题意得,直线为线段的垂直平分线,则,的周长为,即可得出答案.
本题考查作图基本作图、线段垂直平分线的性质,熟练掌握线段垂直平分线的性质是解答本题的关键.
9.【答案】
【解析】解:设,
,
,
,
,
,
,
,
,
,
,
,
,
,
,,
,
故选:.
设,利用等腰三角形的性质可得,从而利用三角形的外角性质可得,再利用等腰三角形的性质可得,从而利用三角形的外角性质可得,然后利用等腰三角形的性质可得,从而利用三角形内角和定理列出关于的方程,进行计算可求出,,最后利用角的和差关系进行计算,即可解答.
10.【答案】
【解析】解:四边形是菱形,
,
,
是等边三角形,
,
,
,
,
,
∽,
故正确;
,
,
,
故错误;
如图,作交的延长线于点,
在中,,,,
,,,
,
故正确;
设,,则,
∽,
,
故正确,
故选:.
根据一线三等角基本模型可得∽,可知正确;根据相似三角形的性质可得,再利用三角形内角和定理可知错误;作交的延长线于点,利用含角的直角三角形的性质得,,,再根据勾股定理可得的长,则正确;设,,则,利用相似三角形的周长比等于相似比可得答案.
11.【答案】
【解析】解:由题意可得,,
去分母得,,
去括号得,,
移项得,,
合并同类项得,,
系数化为得,,
的取值范围为.
故答案为:.
12.【答案】
【解析】解:根据题意,得,
解得,
故答案为:.
13.【答案】
【解析】解:过点作轴于点,如图所示:
则,
,
在矩形中,,
,
,
,
,
∽,
:::,
,
:::,
直线与轴,轴分别相交于,两点,
当时,,
点坐标为,
,
当时,,
点坐标为,
,
,
,
点坐标为,
反比例函数经过第二象限内的,两点,
,
故答案为:.
14.【答案】
【解析】解:由题意得:,
.
抛物线的开口方向向上,
.
.
抛物线与轴的交点在轴的负半轴,
.
.
的结论正确;
方程的解是,,
抛物线与直线的交点的横坐标为,,
对称轴为直线,抛物线与轴交于点,
抛物线与轴的另一个交点为,
抛物线开口向上,
,,
的结论正确;
抛物线是常数,的顶点坐标是,
二次函数有最小值.
抛物线与直线没有公共点.
方程无解.
即方程没有实数根.
的结论错误;
抛物线是常数,的顶点坐标是,
.
,
,
,
,
,
的结论错误.
综上,正确的结论为:,
故答案为:.
15.【答案】解:
;
,
解不等式,得,
解不等式,得,
所以不等式组的解集是,
所以不等式组的整数解是,.
16.【答案】 或
【解析】解:如图,三角形即为所求.
点的坐标为,点的坐标为.
故答案为:;.
设点的坐标为,
则,
解得或,
点的坐标为或.
故答案为:或.
三角形的面积为.
17.【答案】解:设购进甲种商品件,乙种商品件,
根据题意,得,
解得,
答:该商场购进甲种商品件,乙种商品件.
18.【答案】
【解析】解:根据题意得:
元.
故答案为:;
根据题意得:当时,应缴纳水费元;
当时,应缴纳水费元;
当时,应缴纳水费元.
应缴纳水费元;
设小红家月份的用水量为,则月份的用水量为.
当时,,
解得:;
当时,,
解得:不符合题意,舍去.
,
,
小红家月份的用水量为,月份的用水量为.
故答案为:,.
19.【答案】解:直径的长为,
,
为的切线,
,
,
,
,
;
证明:,
,
,
,
,
.
20.【答案】解:过点作,垂足为,
由题意得:,,,,,
,
在中,,
,
,
在中,,
,
大楼的高为.
21.【答案】
【解析】解:本次调查一共随机抽取的学生总人数为:名,
组的人数为:名,
,
所抽取学生成绩的中位数是第个和第个成绩的平均数,,
所抽取学生成绩的中位数落在组,
故答案为:,;
组的人数为:人,
补全学生成绩频数分布直方图如下:
人,
答:估计该校成绩优秀的学生有人.
22.【答案】证明:如图,延长至点,则,
,
,
,
;
证明:如图,在上截取,连接,
,
四边形为平行四边形,
,,
,
,
,
,
∽,
::,
,
,
;
解:设,,
,,,
∽,
::,
即,
即,
,
解得负值舍去,
.
::,
,
又,
,
,
由折叠知:,
,
,
,
,
由折叠知:,
,
,
,
,
:::,
,
::,
:,
,
.
23.【答案】解:当时,,
解得,,
,
.
,
,
,
抛物线的解析式为;
如图,作于,
,
,
设,则,
,
,
解得,
,
,
;
如图,作轴,交于,
则,
,
,
,
,
由,可知,直线的解析式为,
设,则,
,
,
时,的最大值为,
的最大值为.
【解析】令可得,,从而得出点、的坐标,即可得出的长,从而得出答案;
作于,设,则,再将点的坐标代入抛物线解析式即可;
作轴,交于,根据,可得,利用铅垂高求出的最大值,进而解决问题.
第20页,共21页
数 学
注意事项:
1.你拿到的试卷满分为150分,考试时间为150分钟;
2.试卷包括“试题卷”和“答题卷”两部分,请务必在“答题卷”上答题,在“试题卷”上答题是无效的;
3.考试结束后,请将“试题卷”和“答题卷”一并交回。
一、选择题(本大题共10小题,每小题4分,共40分。在每小题列出的选项中,选出符合题目的一项)
1. 的绝对值是( )
A. B. C. D.
2. 以反映伟大抗美援朝精神为题材的电影长津湖,作为国庆献礼片,截止到年月底,票房已突破亿,试用科学记数法表示亿为( )
A. B. C. D.
3. 如图,是由个同样大小的正方体摆成的几何体,将正方体移走后,所得几何体( )
A. 主视图不变,左视图改变
B. 主视图不变,左视图不变
C. 主视图改变,左视图不变
D. 主视图改变,左视图改变
4. 下列计算正确的是( )
A. B. C. D.
5. 阳光中学举行学生运动会,小汪和小勇参加了米跑.路程单位:米与时间单位:分钟之间的函数图象如图所示,两位同学在跑步中均保持匀速,则下列说法错误的是( )
A. 小勇的平均速度为米分
B. 到终点前分钟,小汪的速度比小勇的速度快米分
C. 小勇和小汪同时达到终点
D. 小汪和小勇的平均速度相等
6. “宫商角徵羽”是中国古乐的五个基本音阶相当于西乐的,,,,,是采用“三分损益法”通过数学方法获得现有一款“一起听古音”的音乐玩具,音乐小球从处沿轨道进入小洞就可以发出相应的声音,且小球进入每个小洞中可能性大小相同现有一个音乐小球从处先后两次进入小洞,先发出“商”音,再发出“羽”音的概率是( )
A. B. C. D.
7. 如图,在中,,,点,分别在和上,,若以为直径的交的中点,可知的直径是( )
A.
B.
C.
D.
8. 如图,在中,分别以,为圆心,大于长为半径作弧,两弧分别相交于,两点,作直线,分别交线段,于点,,若,的周长为,则的长度为( )
A. B. C. D.
9. 如图,在中,,点,分别在,上,且,,则的度数是( )
A.
B.
C.
D.
10. 如图,在菱形中,,点、是边、上任意两点,将菱形沿翻折,点恰巧落在对角线上的点处,下列结论:
∽
若,则
若菱形边长为,是的中点,连结,则线段
若::,则::,其中正确结论的个数是( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
11. 对于实数,,我们定义符号的意义为:当时,;当时,,如:,,时,则的取值范围为 .
12. 已知关于的一元二次方程有两个实数根,则的取值范围是 .
13. 如图,直线与轴,轴分别相交于,两点,为边作矩形,,反比例函数经过第二象限内的,两点,则的值是 .
14. 如图,已知抛物线为常数,的顶点为,抛物线与轴交于点,则下列结论:;若方程的解是,,且满足,则,;关于的方程有两个不等的实数根;其中,正确的结论有 .
三、解答题(本大题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤)
15. 分
计算:;
解不等式组:,并写出它的所有整数解.
16. 分
如图,,,将三角形向右平移个单位长度,然后再向上平移个单位长度,可以得到三角形.
画出平移后的三角形,三角形的顶点的坐标为 ;顶点的坐标为 ;
已知点在轴上,以,,为顶点的三角形面积为,则点的坐标为 ;
求三角形的面积.
17. 分
某商场销售甲、乙两种商品,其中甲种商品进价为元件,售价为元件;乙种商品进价为元件,售价为元件现商场用元购进这两种商品并全部售出,两种商品的总利润为元,问该商场购进甲、乙两种商品各多少件?
18. 分
某市采用分段收费的方式按月计算每户家庭的水费,收费标准如表:
户月用水量 收费标准元
不超过
超过,但不超过的部分
超过的部分
小明家月份用水量为,应缴纳水费 元;
设某户某月的用水量为,应缴纳水费多少元?用含的代数式表示
小红家月份和月份的用水量共,且月份用水量比月份多,这两个月共缴纳水费元,则小红家月份和月份的用水量分别为 , .
19. 分
如图,是的外接圆,直径的长为,过点的切线交的延长线于点,连接.
若,求的长;
若,求证:.
20. 分
如图,大楼底部堆放着一堆装修垃圾,在装修垃圾的旁边有一幢别墅,在别墅的顶端处测得装修垃圾边缘点的俯角为,测得大楼顶端的仰角为点,,在同一水平直线上已知,装修垃圾底部,求大楼的高.
21. 分
年月日,“天宫课堂”第三课开讲为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下组满分分,组:,组:,组:,组:,组:,并绘制了如图不完整的统计图请结合统计图,解答下列问题:
频数分布直方图中 ,所抽取学生成绩的中位数落在 组;
补全学生成绩频数分布直方图;
若成绩在分及以上为优秀,学校共有名学生,估计该校成绩优秀的学生有多少人?
22. 分
如图,为四边形的对角线,与关于直线对称,经过的中点,连接,.
求证:;
若,求证:;
如图,在的条件下,连接交于点,若,求的长.
23. 分
已知:如图,二次函数与轴交于点,,点在点左侧,交轴于点,.
求抛物线的解析式;
在第一象限的抛物线上有一点,连接,若,求点坐标;
点在第一象限的抛物线上,于点,求的最大值?
答案和解析
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
【解析】解:根据题意画图如下:
共有种等可能的情况数,其中先发出“商”音,再发出“羽”音的有种,
则先发出“商”音,再发出“羽”音的概率是.
故选:.
画树状图,共有种等可能的结果,其中先发出“商”音,再发出“羽”音的结果有种,再由概率公式求解即可.
本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.掌握概率公式:概率所求情况数与总情况数之比是解题的关键.
7.【答案】
【解析】解:如图,连接,
,是的中点,,
,,,
,
是的直径,
,
,
≌,
,
由勾股定理得:.
故选:.
8.【答案】
【解析】解:由题意得,直线为线段的垂直平分线,
,
的周长为,
.
故答案为:.
由题意得,直线为线段的垂直平分线,则,的周长为,即可得出答案.
本题考查作图基本作图、线段垂直平分线的性质,熟练掌握线段垂直平分线的性质是解答本题的关键.
9.【答案】
【解析】解:设,
,
,
,
,
,
,
,
,
,
,
,
,
,
,,
,
故选:.
设,利用等腰三角形的性质可得,从而利用三角形的外角性质可得,再利用等腰三角形的性质可得,从而利用三角形的外角性质可得,然后利用等腰三角形的性质可得,从而利用三角形内角和定理列出关于的方程,进行计算可求出,,最后利用角的和差关系进行计算,即可解答.
10.【答案】
【解析】解:四边形是菱形,
,
,
是等边三角形,
,
,
,
,
,
∽,
故正确;
,
,
,
故错误;
如图,作交的延长线于点,
在中,,,,
,,,
,
故正确;
设,,则,
∽,
,
故正确,
故选:.
根据一线三等角基本模型可得∽,可知正确;根据相似三角形的性质可得,再利用三角形内角和定理可知错误;作交的延长线于点,利用含角的直角三角形的性质得,,,再根据勾股定理可得的长,则正确;设,,则,利用相似三角形的周长比等于相似比可得答案.
11.【答案】
【解析】解:由题意可得,,
去分母得,,
去括号得,,
移项得,,
合并同类项得,,
系数化为得,,
的取值范围为.
故答案为:.
12.【答案】
【解析】解:根据题意,得,
解得,
故答案为:.
13.【答案】
【解析】解:过点作轴于点,如图所示:
则,
,
在矩形中,,
,
,
,
,
∽,
:::,
,
:::,
直线与轴,轴分别相交于,两点,
当时,,
点坐标为,
,
当时,,
点坐标为,
,
,
,
点坐标为,
反比例函数经过第二象限内的,两点,
,
故答案为:.
14.【答案】
【解析】解:由题意得:,
.
抛物线的开口方向向上,
.
.
抛物线与轴的交点在轴的负半轴,
.
.
的结论正确;
方程的解是,,
抛物线与直线的交点的横坐标为,,
对称轴为直线,抛物线与轴交于点,
抛物线与轴的另一个交点为,
抛物线开口向上,
,,
的结论正确;
抛物线是常数,的顶点坐标是,
二次函数有最小值.
抛物线与直线没有公共点.
方程无解.
即方程没有实数根.
的结论错误;
抛物线是常数,的顶点坐标是,
.
,
,
,
,
,
的结论错误.
综上,正确的结论为:,
故答案为:.
15.【答案】解:
;
,
解不等式,得,
解不等式,得,
所以不等式组的解集是,
所以不等式组的整数解是,.
16.【答案】 或
【解析】解:如图,三角形即为所求.
点的坐标为,点的坐标为.
故答案为:;.
设点的坐标为,
则,
解得或,
点的坐标为或.
故答案为:或.
三角形的面积为.
17.【答案】解:设购进甲种商品件,乙种商品件,
根据题意,得,
解得,
答:该商场购进甲种商品件,乙种商品件.
18.【答案】
【解析】解:根据题意得:
元.
故答案为:;
根据题意得:当时,应缴纳水费元;
当时,应缴纳水费元;
当时,应缴纳水费元.
应缴纳水费元;
设小红家月份的用水量为,则月份的用水量为.
当时,,
解得:;
当时,,
解得:不符合题意,舍去.
,
,
小红家月份的用水量为,月份的用水量为.
故答案为:,.
19.【答案】解:直径的长为,
,
为的切线,
,
,
,
,
;
证明:,
,
,
,
,
.
20.【答案】解:过点作,垂足为,
由题意得:,,,,,
,
在中,,
,
,
在中,,
,
大楼的高为.
21.【答案】
【解析】解:本次调查一共随机抽取的学生总人数为:名,
组的人数为:名,
,
所抽取学生成绩的中位数是第个和第个成绩的平均数,,
所抽取学生成绩的中位数落在组,
故答案为:,;
组的人数为:人,
补全学生成绩频数分布直方图如下:
人,
答:估计该校成绩优秀的学生有人.
22.【答案】证明:如图,延长至点,则,
,
,
,
;
证明:如图,在上截取,连接,
,
四边形为平行四边形,
,,
,
,
,
,
∽,
::,
,
,
;
解:设,,
,,,
∽,
::,
即,
即,
,
解得负值舍去,
.
::,
,
又,
,
,
由折叠知:,
,
,
,
,
由折叠知:,
,
,
,
,
:::,
,
::,
:,
,
.
23.【答案】解:当时,,
解得,,
,
.
,
,
,
抛物线的解析式为;
如图,作于,
,
,
设,则,
,
,
解得,
,
,
;
如图,作轴,交于,
则,
,
,
,
,
由,可知,直线的解析式为,
设,则,
,
,
时,的最大值为,
的最大值为.
【解析】令可得,,从而得出点、的坐标,即可得出的长,从而得出答案;
作于,设,则,再将点的坐标代入抛物线解析式即可;
作轴,交于,根据,可得,利用铅垂高求出的最大值,进而解决问题.
第20页,共21页
同课章节目录
