19.2一次函数(第7课时)
文档属性
| 名称 | 19.2一次函数(第7课时) |  | |
| 格式 | zip | ||
| 文件大小 | 452.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-29 07:22:41 | ||
图片预览




文档简介
课件11张PPT。 第7课时 一次函数
与一元一次不等式
教学目标知识与技能:掌握一元一次不等式与一次函数的关系,会运用函数解决不等式有关问题。
过程与方法:通过具体问题初步体会一次函数的变化规律与一元一次不等式解集的联系。
情感、态度与价值观:感知不等式、函数、方程的不同作用与内在联系,并体会分类讨论的数学思想。自学指导:阅读教材96页思考:
1、你能得到“解不等式5x+6>3x+10”与“求自变量x为何值时,不等式函数y=2x-4的值大于0”有什么关系?
2、学习不等式和一次函数的关系有什么意义?
探究新知:解:(1)把5x+6>3x+10转化为2x-4>0,解得x >2
⑵就是要解不等式2x-4>0, 解得x >2时
函数y=2x-4的值大于0
(1)解不等式:5x+6>3x+10
(2)当x为何值时,函数y=2x-4的值大于0议一议:在上面的问题解
决过程中,你能发现它们
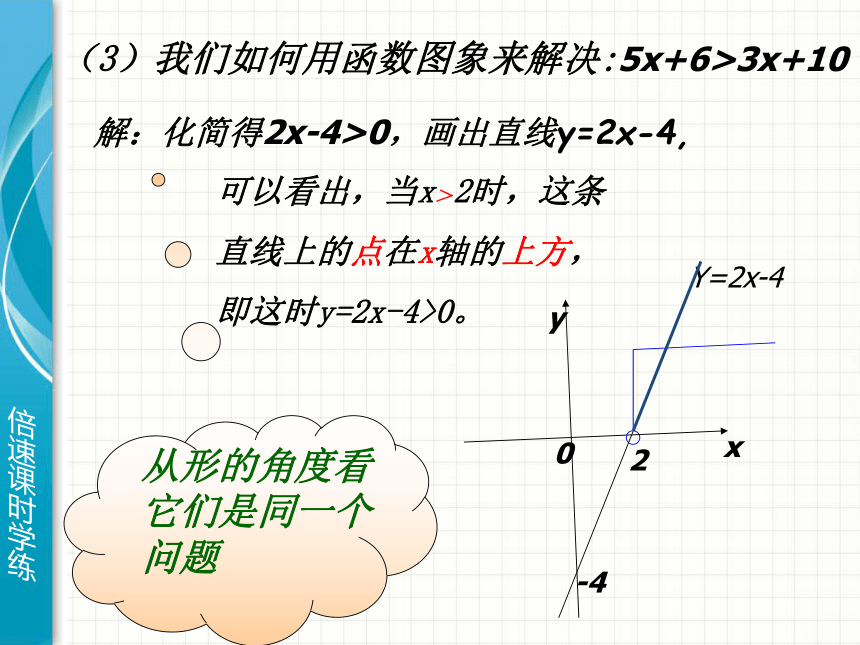
之间有什么关系吗?从数的角度看它们是同一个问题的两种不同表达方式(3)我们如何用函数图象来解决:5x+6>3x+10
解:化简得2x-4>0,画出直线y=2x-4,可以看出,当x>2时,这条
直线上的点在x轴的上方,
即这时y=2x-4>0。
从形的角度看它们是同一个问题 根据下列一次函数的图象,你能写出哪些不等式?并直接写出相应的不等式的解集。3x+6>0 ( x>- 2)3x+6<0 ( x<- 2)
3x+6≥0 ( x ≥- 2)3x+6≤0 ( x ≤ - 2)
尝试练习可以看出,当x<2时这条直线上的点在x轴的下方,解(方法一):化简得3x-6<0,画出直线y=3x-6,即这时y=3x-6<0,所以不等式的解集为x<2
用两种画函数图象的方法解不等式 5x+4<2x+10
拓展延伸:
解(方法二):将原不等式的两边分别看成两个一次函数,画出直线y1=5x+4与直线y2=2x+10的图像,可以看出,它们交点的横坐标为2,当X<2时,对于同一个X,直线
Y=5X+4上的点在直线
Y=2X+10上相应点的下方,这时
5X+4 < 2X+10,所以不等式的解集为X<2。你能有几种方法解不等式
5x+4<2x+10-22、如图,直线L1, L2交于一点P,若y1 ≥y2 ,则( )
x ≥ 3
x ≤3
2 ≤ x ≤ 3
x ≤ 4
3、完成试卷P71-72页1、已知函数Y=3X+8,当X————————,函数
的值等于0。当X————————,函数的值大于0。当X———————— ,函数的值不大于2。= ≤- 2>B巩固练习五.小结一下 1、通过本节课所学内容你认为一次函数、一元一次方程、一 元一次不等式有何关系?
2、你对用一次函数图像来解一元一次不等式有何感受?
课堂小结再见
过程与方法:通过具体问题初步体会一次函数的变化规律与一元一次不等式解集的联系。
情感、态度与价值观:感知不等式、函数、方程的不同作用与内在联系,并体会分类讨论的数学思想。自学指导:阅读教材96页思考:
1、你能得到“解不等式5x+6>3x+10”与“求自变量x为何值时,不等式函数y=2x-4的值大于0”有什么关系?
2、学习不等式和一次函数的关系有什么意义?
探究新知:解:(1)把5x+6>3x+10转化为2x-4>0,解得x >2
⑵就是要解不等式2x-4>0, 解得x >2时
函数y=2x-4的值大于0
(1)解不等式:5x+6>3x+10
(2)当x为何值时,函数y=2x-4的值大于0议一议:在上面的问题解
决过程中,你能发现它们
之间有什么关系吗?从数的角度看它们是同一个问题的两种不同表达方式(3)我们如何用函数图象来解决:5x+6>3x+10
解:化简得2x-4>0,画出直线y=2x-4,可以看出,当x>2时,这条
直线上的点在x轴的上方,
即这时y=2x-4>0。
从形的角度看它们是同一个问题 根据下列一次函数的图象,你能写出哪些不等式?并直接写出相应的不等式的解集。3x+6>0 ( x>- 2)3x+6<0 ( x<- 2)
3x+6≥0 ( x ≥- 2)3x+6≤0 ( x ≤ - 2)
尝试练习可以看出,当x<2时这条直线上的点在x轴的下方,解(方法一):化简得3x-6<0,画出直线y=3x-6,即这时y=3x-6<0,所以不等式的解集为x<2
用两种画函数图象的方法解不等式 5x+4<2x+10
拓展延伸:
解(方法二):将原不等式的两边分别看成两个一次函数,画出直线y1=5x+4与直线y2=2x+10的图像,可以看出,它们交点的横坐标为2,当X<2时,对于同一个X,直线
Y=5X+4上的点在直线
Y=2X+10上相应点的下方,这时
5X+4 < 2X+10,所以不等式的解集为X<2。你能有几种方法解不等式
5x+4<2x+10-22、如图,直线L1, L2交于一点P,若y1 ≥y2 ,则( )
x ≥ 3
x ≤3
2 ≤ x ≤ 3
x ≤ 4
3、完成试卷P71-72页1、已知函数Y=3X+8,当X————————,函数
的值等于0。当X————————,函数的值大于0。当X———————— ,函数的值不大于2。= ≤- 2>B巩固练习五.小结一下 1、通过本节课所学内容你认为一次函数、一元一次方程、一 元一次不等式有何关系?
2、你对用一次函数图像来解一元一次不等式有何感受?
课堂小结再见
