21.3.5实际问题与一元二次方程(动点问题)
文档属性
| 名称 | 21.3.5实际问题与一元二次方程(动点问题) |  | |
| 格式 | zip | ||
| 文件大小 | 166.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-27 23:51:52 | ||
图片预览



文档简介
课件10张PPT。实际问题与一元二次方程(五)动点问题每日一练用适当的方法解方程有关“动点”的运动问题”1)关键—— 以静代动
把动的点进行转换,变为线段的长度, 2)方法—— 时间变路程
求“动点的运动时间”可以转化为求“动点的运动路程”,也是求线段的长度;由此,学会把动点的问题转化为静点的问题,
是解这类问题的关键.3)常找的数量关系——
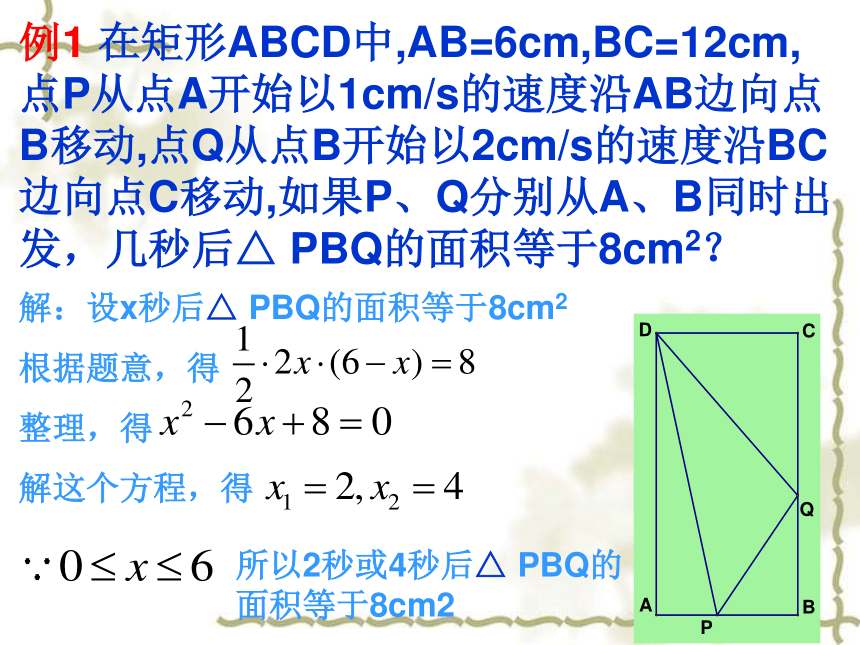
面积,勾股定理等;例1 在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向点B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移动,如果P、Q分别从A、B同时出发,几秒后△ PBQ的面积等于8cm2?解:设x秒后△ PBQ的面积等于8cm2
根据题意,得
整理,得
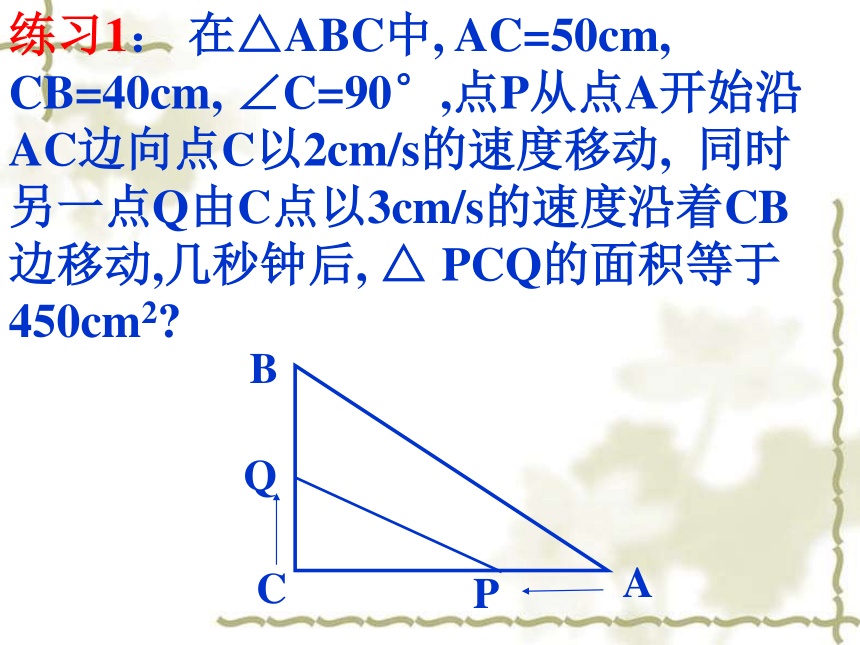
解这个方程,得所以2秒或4秒后△ PBQ的面积等于8cm2练习1: 在△ABC中, AC=50cm, CB=40cm, ∠C=90°,点P从点A开始沿AC边向点C以2cm/s的速度移动, 同时另一点Q由C点以3cm/s的速度沿着CB边移动,几秒钟后, △ PCQ的面积等于450cm2?QBACP例2:等腰直角 △A B中,AB=BC=8cm,动点P从A点出发,沿AB向B移动,经过点P引平行于BC,AC的直线与AC,BC分别交于R、Q.当AP等于多少厘米时,平行四边形PQCR的面积等于16cm2?练习2:在直角三角形ABC中,AB=BC=12cm,点D从点A开始以2cm/s的速度沿AB边向点B移动,过点D做DE平行于BC,DF平行于AC,点E.F分别在AC,BC上,问:点D出发几秒后四边形DFCE的面积为20cm2?例3: △ ABC中,AB=3, ∠ BAC=45°,CD⊥ AB,垂足为D,CD=2,P是AB上的一动点(不与A,B重合),且AP=x,过点P作直线l与AB垂直.
i)设△ ABC位于直线l左侧部分的面积为S,写出S与x之间的函数关系式;
ii)当x为何值时,直线l平分△ ABC的面积? 例4:客轮沿折线A-B-C从A出发经B再到C匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批物品送达客轮,两船若同时起航,并同时到达折线A-B-C上的某点E处,已知AB=BC=200海里, ∠ABC=90°,客轮速度是货轮速度的2倍.
(1)选择:两船相遇之处E点( )
A.在线段AB上;
B.在线段BC上;
C.可以在线段AB上,也可以在线段BC上;ii)求货轮从出发到两船相遇共航行了多少海里?(结果保留根号)解:设货轮从出发到两船相遇共航行了x海里,过D作DF⊥ CB,交BD于F,则DE=x,AB+BE=2x,DF=100,EF=300-2x
在Rt⊿DEF 中,
把动的点进行转换,变为线段的长度, 2)方法—— 时间变路程
求“动点的运动时间”可以转化为求“动点的运动路程”,也是求线段的长度;由此,学会把动点的问题转化为静点的问题,
是解这类问题的关键.3)常找的数量关系——
面积,勾股定理等;例1 在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向点B移动,点Q从点B开始以2cm/s的速度沿BC边向点C移动,如果P、Q分别从A、B同时出发,几秒后△ PBQ的面积等于8cm2?解:设x秒后△ PBQ的面积等于8cm2
根据题意,得
整理,得
解这个方程,得所以2秒或4秒后△ PBQ的面积等于8cm2练习1: 在△ABC中, AC=50cm, CB=40cm, ∠C=90°,点P从点A开始沿AC边向点C以2cm/s的速度移动, 同时另一点Q由C点以3cm/s的速度沿着CB边移动,几秒钟后, △ PCQ的面积等于450cm2?QBACP例2:等腰直角 △A B中,AB=BC=8cm,动点P从A点出发,沿AB向B移动,经过点P引平行于BC,AC的直线与AC,BC分别交于R、Q.当AP等于多少厘米时,平行四边形PQCR的面积等于16cm2?练习2:在直角三角形ABC中,AB=BC=12cm,点D从点A开始以2cm/s的速度沿AB边向点B移动,过点D做DE平行于BC,DF平行于AC,点E.F分别在AC,BC上,问:点D出发几秒后四边形DFCE的面积为20cm2?例3: △ ABC中,AB=3, ∠ BAC=45°,CD⊥ AB,垂足为D,CD=2,P是AB上的一动点(不与A,B重合),且AP=x,过点P作直线l与AB垂直.
i)设△ ABC位于直线l左侧部分的面积为S,写出S与x之间的函数关系式;
ii)当x为何值时,直线l平分△ ABC的面积? 例4:客轮沿折线A-B-C从A出发经B再到C匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批物品送达客轮,两船若同时起航,并同时到达折线A-B-C上的某点E处,已知AB=BC=200海里, ∠ABC=90°,客轮速度是货轮速度的2倍.
(1)选择:两船相遇之处E点( )
A.在线段AB上;
B.在线段BC上;
C.可以在线段AB上,也可以在线段BC上;ii)求货轮从出发到两船相遇共航行了多少海里?(结果保留根号)解:设货轮从出发到两船相遇共航行了x海里,过D作DF⊥ CB,交BD于F,则DE=x,AB+BE=2x,DF=100,EF=300-2x
在Rt⊿DEF 中,
同课章节目录
