4.7正反比例的整理和练习导学案1 六年级数学下册-北师大版(含答案)
文档属性
| 名称 | 4.7正反比例的整理和练习导学案1 六年级数学下册-北师大版(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 723.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-16 00:00:00 | ||
图片预览

文档简介
4.7正反比例的整理和练习
(一)知识梳理
填空:
1、两种量,一种量可以随着另一个种量的变化而变化。而且它们的比值一定,我们就说这两种量成( )。
2、成正比例的两种量的比值是( )的。
3、速度一定时,路程和时间成( )比例。
4、两种量,一种量可以随着另一个种量的变化而变化。而且它们的( )一定,我们就说这两种量成反比例。
5、成反比例的两种量的( )是一定的。
6、判断两种量是否成反比例关键看着两种量的( )是否相等。
7、表示正比例关系的图象是从横轴和竖轴的交点画出的一条( ),相关联两种量的所有对应点都在( )上。
(二)题型、方法归纳与典例精讲
1、正、反比例的意义和判断。
例:下面各题中的两个量,哪些成正比例,哪些成反比例,哪些既不成正比例也不成反比例?
等边三角形的周长和边长。
妙想从家步行到学校的平均速度与所花的时间。
每年体检,你们班视力正常的人与近视的人数。
2、正、反比例的应用。
例:给一间教室铺地砖,每块地砖的面积与所需地砖的数量如下。
每块地砖的面积和所需地砖的数量有什么关系?
如果每块地砖的面积是0.5平方米,铺这一地面需要多少块地砖?
铺这一地面用了500块地砖,所用的地砖每块面积是多大?
随堂检测
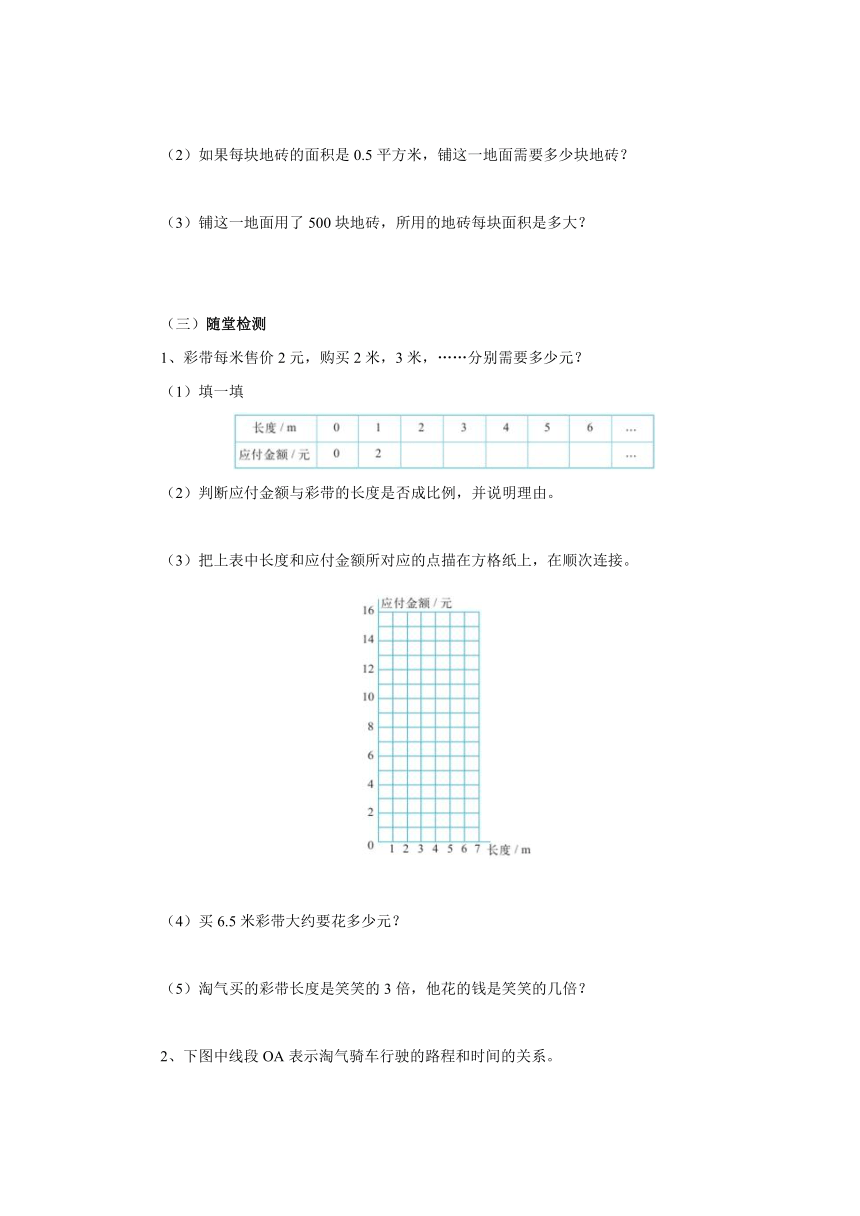
1、彩带每米售价2元,购买2米,3米,……分别需要多少元?
填一填
判断应付金额与彩带的长度是否成比例,并说明理由。
把上表中长度和应付金额所对应的点描在方格纸上,在顺次连接。
买6.5米彩带大约要花多少元?
淘气买的彩带长度是笑笑的3倍,他花的钱是笑笑的几倍?
下图中线段OA表示淘气骑车行驶的路程和时间的关系。
请根据上图回答下列问题。
淘气骑车行驶了多长时间?行驶了多少千米?
骑车1.5时,淘气行驶了多长千米?
行驶30千米,淘气用了多长时间?
淘气骑车的速度是多少?
用36个边长为1厘米的小正方形,你能拼成几种不同的长方形?
从表中,你能发现长和宽有怎样的关系吗?与同伴进行交流。
参考答案
知识梳理
正比例;2、一定;3、正比例;4、积;5、积;6、积;7、射线 射线
题型、方法归纳与典例精讲
1、(1)成正比例
(2)成反比例
(3)既不成正比例,也不成反比例。
2、(1)每块地砖的面积和所需要的数量成反比例
(2)0.2×600÷0.5=240(块)
答:铺这一地面需要240块地砖。
(3)0.2×600÷500=0.24(平方米)
答:所用的地砖每块面积是0.24平方米。
随堂检测
(1)
(2)应付金额与彩带的长度成比例。应付金额与彩带的长度的比值一定。
(3)
(4)买6.5米彩带大约要花13元。
(5)他花的钱是笑笑的3倍。
(1)淘气骑车行驶了2时,行驶了30千米。
(2)骑车1.5时,淘气行驶了22.5千米。
(3)行驶30千米,淘气用了2时。
(4)淘气骑车的速度是15千米/时。
3、
面积一定时,长方形的长和宽成反比例。
(一)知识梳理
填空:
1、两种量,一种量可以随着另一个种量的变化而变化。而且它们的比值一定,我们就说这两种量成( )。
2、成正比例的两种量的比值是( )的。
3、速度一定时,路程和时间成( )比例。
4、两种量,一种量可以随着另一个种量的变化而变化。而且它们的( )一定,我们就说这两种量成反比例。
5、成反比例的两种量的( )是一定的。
6、判断两种量是否成反比例关键看着两种量的( )是否相等。
7、表示正比例关系的图象是从横轴和竖轴的交点画出的一条( ),相关联两种量的所有对应点都在( )上。
(二)题型、方法归纳与典例精讲
1、正、反比例的意义和判断。
例:下面各题中的两个量,哪些成正比例,哪些成反比例,哪些既不成正比例也不成反比例?
等边三角形的周长和边长。
妙想从家步行到学校的平均速度与所花的时间。
每年体检,你们班视力正常的人与近视的人数。
2、正、反比例的应用。
例:给一间教室铺地砖,每块地砖的面积与所需地砖的数量如下。
每块地砖的面积和所需地砖的数量有什么关系?
如果每块地砖的面积是0.5平方米,铺这一地面需要多少块地砖?
铺这一地面用了500块地砖,所用的地砖每块面积是多大?
随堂检测
1、彩带每米售价2元,购买2米,3米,……分别需要多少元?
填一填
判断应付金额与彩带的长度是否成比例,并说明理由。
把上表中长度和应付金额所对应的点描在方格纸上,在顺次连接。
买6.5米彩带大约要花多少元?
淘气买的彩带长度是笑笑的3倍,他花的钱是笑笑的几倍?
下图中线段OA表示淘气骑车行驶的路程和时间的关系。
请根据上图回答下列问题。
淘气骑车行驶了多长时间?行驶了多少千米?
骑车1.5时,淘气行驶了多长千米?
行驶30千米,淘气用了多长时间?
淘气骑车的速度是多少?
用36个边长为1厘米的小正方形,你能拼成几种不同的长方形?
从表中,你能发现长和宽有怎样的关系吗?与同伴进行交流。
参考答案
知识梳理
正比例;2、一定;3、正比例;4、积;5、积;6、积;7、射线 射线
题型、方法归纳与典例精讲
1、(1)成正比例
(2)成反比例
(3)既不成正比例,也不成反比例。
2、(1)每块地砖的面积和所需要的数量成反比例
(2)0.2×600÷0.5=240(块)
答:铺这一地面需要240块地砖。
(3)0.2×600÷500=0.24(平方米)
答:所用的地砖每块面积是0.24平方米。
随堂检测
(1)
(2)应付金额与彩带的长度成比例。应付金额与彩带的长度的比值一定。
(3)
(4)买6.5米彩带大约要花13元。
(5)他花的钱是笑笑的3倍。
(1)淘气骑车行驶了2时,行驶了30千米。
(2)骑车1.5时,淘气行驶了22.5千米。
(3)行驶30千米,淘气用了2时。
(4)淘气骑车的速度是15千米/时。
3、
面积一定时,长方形的长和宽成反比例。
