2014年中考专题(数学)-.静态几何之图形的镶嵌和几何体的展开问题探讨
文档属性
| 名称 | 2014年中考专题(数学)-.静态几何之图形的镶嵌和几何体的展开问题探讨 |  | |
| 格式 | zip | ||
| 文件大小 | 273.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-27 23:56:57 | ||
图片预览



文档简介
【备战中考数学专题讲解】
静态几何之图形的镶嵌和几何体的展开问题探讨
平面图形的镶嵌:用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙,不重叠地铺成一片,这就是平面图形的密铺,又称作平面图形的镶嵌。平面镶嵌的条件:各个顶点处内角和恰好为360度。
有些几何体的表面,可以展开成平面图形,这个平面图形称为相应几何体的表面展开图。有时可能得到几种不同的展开图形。
结合2013年全国各地中考的实例,我们从三方面进行静态几何之图形的镶嵌和几何体的展开问题的探讨:
(1)平面图形的镶嵌和剪拼问题;
(2)几何体的展开问题;
(3)几何体展开图的折叠问题。
一、平面图形的镶嵌和剪拼问题:
典型例题:
1.只用下列图形中的一种,能够进行平面镶嵌的是【 】
A.正十边形 B.正八边形 C.正六边形 D.正五边形
2. 用下列一种多边形不能铺满地面的是【 】
A.正方形 B.正十边形 C.正六边形 D.等边三角形
3. 如图,有一张一个角为30°,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是【 】
A.8或 B.10或 C.10或 D.8或
4. 下列图形中,单独选用一种图形不能进行平面镶嵌的是【 】
A.正三角形 B.正六边形 C.正方形 D.正五边形
5. 有3张边长为a的正方形纸片,4张边长分别为a、b(b>a)的矩形纸片,5张边长为b的正方形纸片,从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(按原纸张进行无空隙、无重叠拼接),则拼成的正方形的边长最长可以为【 】
A.a+b B.2a+b C.3a+b D.a+2b
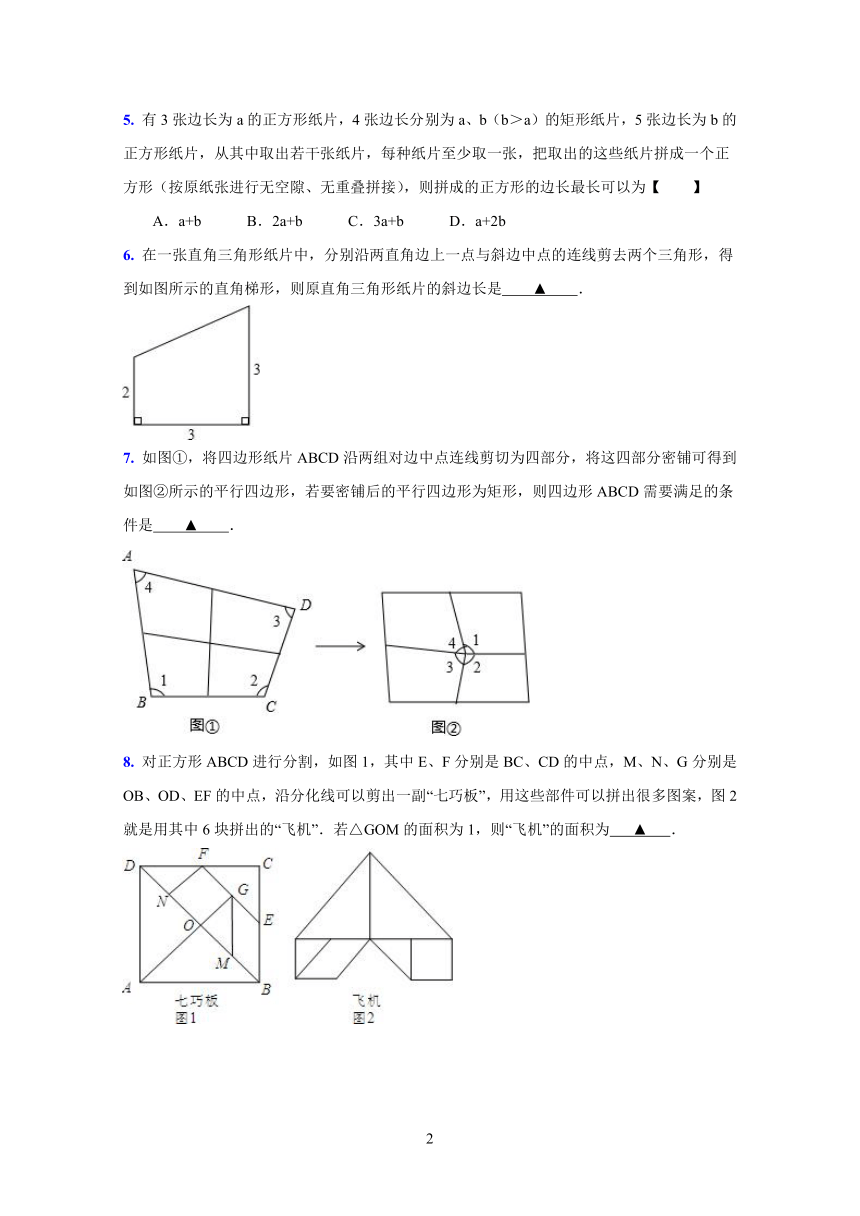
6. 在一张直角三角形纸片中,分别沿两直角边上一点与斜边中点的连线剪去两个三角形,得到如图所示的直角梯形,则原直角三角形纸片的斜边长是 ▲ .
7. 如图①,将四边形纸片ABCD沿两组对边中点连线剪切为四部分,将这四部分密铺可得到如图②所示的平行四边形,若要密铺后的平行四边形为矩形,则四边形ABCD需要满足的条件是 ▲ .
8. 对正方形ABCD进行分割,如图1,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分化线可以剪出一副“七巧板”,用这些部件可以拼出很多图案,图2就是用其中6块拼出的“飞机”.若△GOM的面积为1,则“飞机”的面积为 ▲ .
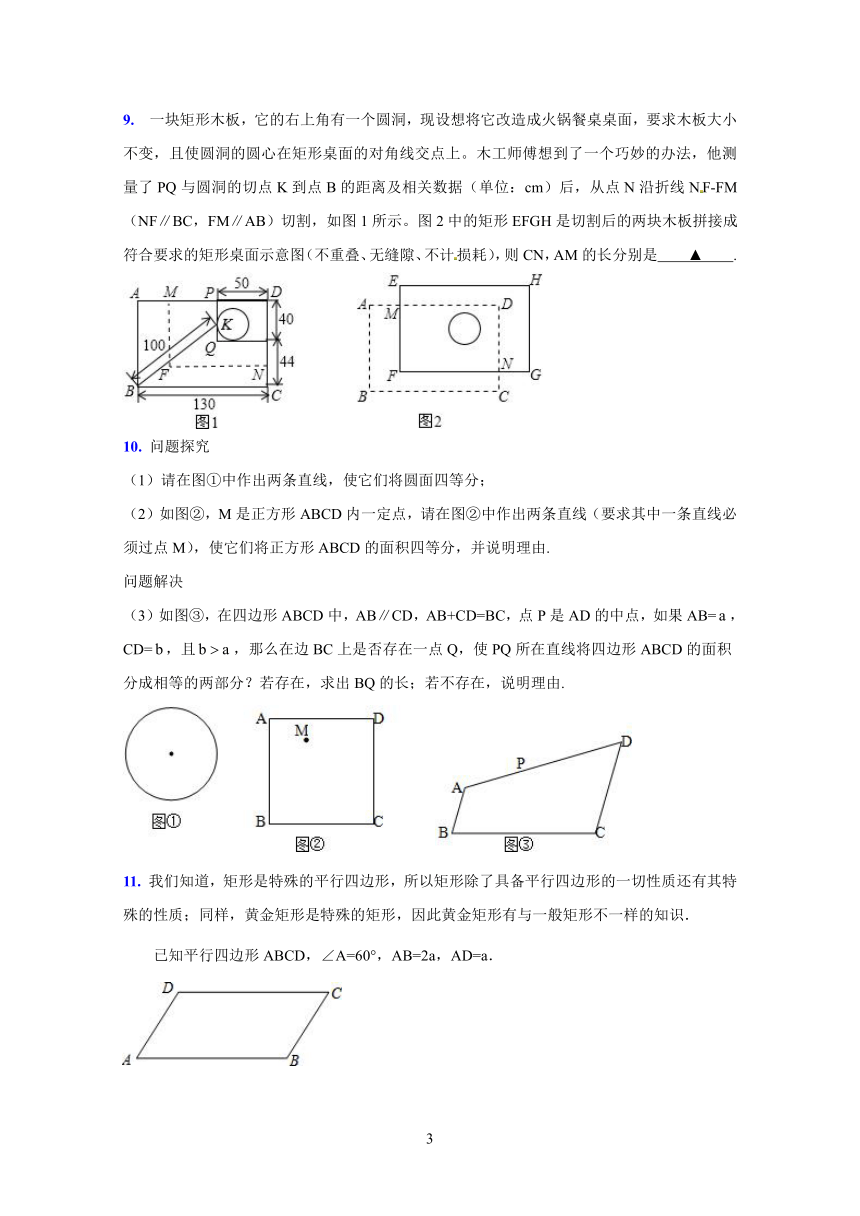
9. 一块矩形木板,它的右上角有一个圆洞,现设想将它改造成火锅餐桌桌面,要求木板大小不变,且使圆洞的圆心在矩形桌面的对角线交点上。木工师傅想到了一个巧妙的办法,他测量了PQ与圆洞的切点K到点B的距离及相关数据(单位:cm)后,从点N沿折线NF-FM(NF∥BC,FM∥AB)切割,如图1所示。图2中的矩形EFGH是切割后的两块木板拼接成符合要求的矩形桌面示意图(不重叠、无缝隙、不计损耗),则CN,AM的长分别是 ▲ .
10. 问题探究
(1)请在图①中作出两条直线,使它们将圆面四等分;
(2)如图②,M是正方形ABCD内一定点,请在图②中作出两条直线(要求其中一条直线必须过点M),使它们将正方形ABCD的面积四等分,并说明理由.
问题解决
(3)如图③,在四边形ABCD中,AB∥CD,AB+CD=BC,点P是AD的中点,如果AB=,CD=,且,那么在边BC上是否存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分?若存在,求出BQ的长;若不存在,说明理由.
11. 我们知道,矩形是特殊的平行四边形,所以矩形除了具备平行四边形的一切性质还有其特殊的性质;同样,黄金矩形是特殊的矩形,因此黄金矩形有与一般矩形不一样的知识.
已知平行四边形ABCD,∠A=60°,AB=2a,AD=a.
(1)把所给的平行四边形ABCD用两种方式分割并作说明(见题答卡表格里的示例);
要求:用直线段分割,分割成的图形是学习过的特殊图形且不超出四个.
(2)图中关于边、角和对角线会有若干关系或问题.现在请计算两条对角线的长度.
要求:计算对角线BD长的过程中要有必要的论证;直接写出对角线AC的长.
解:在表格中作答
分割图形
分割或图形说明
示例
示例①分割成两个菱形。
②两个菱形的边长都为a,锐角都为60°。
12. 下面给出的正多边形的边长都是20 cm.请分别按下列要求设计一种剪拼方法(用虚线表示你的设计方案,把剪拼线段用粗黑实线,在图中标注出必要的符号和数据,并作简要说明.
(1)将图1中的正方形纸片剪拼成一个底面是正方形的直四棱柱模型,使它的表面积与原正方形面积相等;
(2)将图2中的正三角形纸片剪拼成一个底面是正三角形的直三棱柱模型,使它的表面积与原正三角形的面积相等;
(3)将图3中的正五边形纸片剪拼成一个底面是正五边形的直五棱柱模型,使它的表面积与原正五边形的面积相等.
13. 矩形纸片ABCD中,AB=5,AD=4.
(1)如图1,四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形.你能否在该矩形中裁剪出一个面积最大的正方形,最大面积是多少?说明理由;
(2)请用矩形纸片ABCD剪拼成一个面积最大的正方形.要求:在图2的矩形ABCD中画出裁剪线,并在网格中画出用裁剪出的纸片拼成的正方形示意图(使正方形的顶点都在网格的格点上).
14. 雅安芦山发生7.0级地震后,某校师生准备了一些等腰直角三角形纸片,从每张纸片中剪出一个半圆制作玩具,寄给灾区的小朋友.已知如图,是腰长为4的等腰直角三角形ABC,要求剪出的半圆的直径在△ABC的边上,且半圆的弧与△ABC的其他两边相切,请作出所有不同方案的示意图,并求出相应半圆的半径(结果保留根号).
二、几何体的展开问题:
典型例题:
1.如图是一个长方体包装盒,则它的平面展开图是【 】
A.B.C.D.2.圆锥底面圆的半径为3cm,其侧面展开图是半圆,其圆锥母线长为【 】
A.3cm B.6cm C.9cm D.12cm
一个几何体的三视图如图所示,则该几何体的侧面展开图的面积为【 】
A.6cm2 B.4πcm2 C.6πcm2 D.9πcm2
4. 下列四个图形中,是三棱柱的平面展开图的是【 】
5. 一个圆锥的侧面积是底面积的4倍,则圆锥侧面展开图的扇形的圆心角是【 】
A.60° B.90° C.120° D.180°
6. 已知一个圆柱的侧面展开图为如图所示的矩形,则其底面圆的面积为【 】
A. B. 4 C. 或4 D.2或4
7. 小明为了鼓励芦山地震灾区的学生早日走出阴影,好好学习,制作了一个正方体礼盒(如图).礼盒每个面上各有一个字,连起来组成“芦山学子加油”,其中“芦”的对面是“学”,“加”的对面是“油”,则它的平面展开图可能是【 】
B. C.D.
下列图形中,是圆锥侧面展开图的是【 】
B. C. D.
9. 如图,一个几何体上半部为正四棱椎,下半部为立方体,且有一个面涂有颜色,下列图形中,是该几何体的表面展开图的是【 】
B.
C.D.
10. 已知圆柱的底面半径为3cm,母线长为5cm,则圆柱的侧面积是【 】
A.30cm2 B.30πcm2 C.15cm2 D.15πcm2
如图示一个几何体的三视图,则这个几何体的侧面积是【 】
A.12πcm2 B.8πcm2 C.6πcm2 D.3πcm2
12. 一个立体图形的三视图如图所示,根据图中数据求得这个立体图形的的表面积为【 】
A. B. C. D.
把如图中的三棱柱展开,所得到的展开图是【 】
B.C.D.
14. 一个圆锥的左视图是一个正三角形,则这个圆锥的侧面展开图的圆心角等于【 】
A.60° B.90° C.120° D.180°
15.若圆锥的轴截图为等边三角形,则称此圆锥为正圆锥,则正圆锥的侧面展开图的圆心角是【 】
A.90° B.120° C.150° D.180°
16.已知圆锥底面半径为5cm,高为12cm,则圆锥的侧面展开图的面积是 ▲ .
17.一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图扇形的圆心角是 ▲ .
18.已知圆锥母线长为为5cm,底面半径为3cm,则圆锥的侧面展开图的面积是 ▲ .
19.圆锥的底面半径是1,侧面积是2π,则这个圆锥的侧面展开图的圆心角为 ▲ .
20.圆锥的母线长为6cm,底面周长为5πcm,则圆锥的侧面积为
▲ .
21.高为4,底面半径为3的圆锥,则圆锥的侧面展开图的面积是 ▲ .
22.一圆锥的底面半径为1cm,母线长2cm,则该圆锥的侧面积为 ▲ cm2.
23.已知圆锥的底面周长是10π,其侧面展开后所得扇形的圆心角为90°,则该圆锥的母线长是 ▲ .
24.如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是 ▲ .
25.如图,张老师在上课前用硬纸做了一个无底的圆锥形教具,那么这个教具的用纸面积是
▲ cm2.(不考虑接缝等因素,计算结果用π表示).
26.一个圆锥形零件,高为8cm,底面圆的直径为12cm,则此圆锥的侧面积是 ▲ cm2.
27.如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为
▲ m(容器厚度忽略不计).
28.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 ▲ .
29.底面半径为1,母线长为2的圆锥侧面积为 ▲ .
30.如图,圆锥的侧面展开图是一个半圆,求母线AB与高AO的夹角.参考公式:圆锥的侧面积S=πrl,其中r为底面半径,l为母线长.
三、几何体展开图的折叠问题:
典型例题:
如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“共”字一面的相对面上的字是【 】
美 B.丽 C.家 D.园
将一边长为2的正方形纸片折成四部分,再沿折痕折起来,恰好不能重叠的搭成一个三棱锥,则三棱锥四个面中面积最小的面积是【 】
A.1 B. C. D.
3.如图是一个长方体形状包装盒的表面展开图.折叠制作完成后得到长方体的容积是(包装材料厚度不计)【 】
A.40×40×70 B.70×70×80 C.80×80×80 D.40×70×80
一个正方体的平面展开图如图所示,将它折成正方体后,与汉字“岳”相对的面上的汉字是【 】
建 B.设 C.和 D.谐
5. 用如图所示的扇形纸片制作一个圆锥的侧面,要求圆锥的高是4 cm,底面周长是6π cm,则扇形的半径为【 】
A.3cm B.5cm C.6cm D.8cm
下列图形中,能通过折叠围成一个三棱柱的是【 】
B.C.D.
如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是【 】
大 B.伟 C.国 D.的
8. 用一圆心角为120°,半径为6cm的扇形做成一个圆锥的侧面,这个圆锥的底面的半径是【 】
A.1cm B.2cm C.3cm D.4cm
9. 用半径为3cm,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为【 】
A. B.1.5cm C. D.1cm
10. 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是【 】
美 B.丽 C.云 D.南
10. 下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方形包装盒的是【 】
A.B.C.D.
下列各图形中,经过折叠能围成一个立方体的是【 】
B. C. D.
12. 如图是正方形的一种张开图,其中每个面上都标有一个数字。那么在原正方形中,与数字“2”相对的面上的数字是【 】
(A)1 (B)4 (C)5 (D)6
13. 如图,一扇形纸片,圆心角∠AOB为120°,弦AB的长为cm,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为 ▲ .
14.将半径为4cm的半圆围成一个圆锥,这个圆锥的高为 ▲ cm.
15. 如图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“香”相对的面上的汉字是 ▲ .
16. 用半径为10cm,圆心角为216°的扇形做成一个圆锥的侧面,则这个圆锥的高为
▲ cm.
17. 用一个圆心角为90°,半径为32cm的扇形作为一个圆锥的侧面(接缝处不重叠),则这个圆锥的底面圆的半径为 ▲ cm.
18. 已知一个扇形的半径为60cm,圆心角为150°,用它围成一个圆锥的侧面,那么圆锥的底面半径为 ▲ cm.
19.用一个圆心角为120°,半径为4的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径为 ▲ cm.
20. 如图,如果从半径为5cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高是 ▲ cm.
21. 如图,从半径为9cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为 ▲ cm.
22. 以下三组图形都是由四个等边三角形组成.能折成多面体的选项序号是 ▲ .
23. 如图,从直径为4cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是 ▲ cm.
静态几何之图形的镶嵌和几何体的展开问题探讨
平面图形的镶嵌:用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙,不重叠地铺成一片,这就是平面图形的密铺,又称作平面图形的镶嵌。平面镶嵌的条件:各个顶点处内角和恰好为360度。
有些几何体的表面,可以展开成平面图形,这个平面图形称为相应几何体的表面展开图。有时可能得到几种不同的展开图形。
结合2013年全国各地中考的实例,我们从三方面进行静态几何之图形的镶嵌和几何体的展开问题的探讨:
(1)平面图形的镶嵌和剪拼问题;
(2)几何体的展开问题;
(3)几何体展开图的折叠问题。
一、平面图形的镶嵌和剪拼问题:
典型例题:
1.只用下列图形中的一种,能够进行平面镶嵌的是【 】
A.正十边形 B.正八边形 C.正六边形 D.正五边形
2. 用下列一种多边形不能铺满地面的是【 】
A.正方形 B.正十边形 C.正六边形 D.等边三角形
3. 如图,有一张一个角为30°,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是【 】
A.8或 B.10或 C.10或 D.8或
4. 下列图形中,单独选用一种图形不能进行平面镶嵌的是【 】
A.正三角形 B.正六边形 C.正方形 D.正五边形
5. 有3张边长为a的正方形纸片,4张边长分别为a、b(b>a)的矩形纸片,5张边长为b的正方形纸片,从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(按原纸张进行无空隙、无重叠拼接),则拼成的正方形的边长最长可以为【 】
A.a+b B.2a+b C.3a+b D.a+2b
6. 在一张直角三角形纸片中,分别沿两直角边上一点与斜边中点的连线剪去两个三角形,得到如图所示的直角梯形,则原直角三角形纸片的斜边长是 ▲ .
7. 如图①,将四边形纸片ABCD沿两组对边中点连线剪切为四部分,将这四部分密铺可得到如图②所示的平行四边形,若要密铺后的平行四边形为矩形,则四边形ABCD需要满足的条件是 ▲ .
8. 对正方形ABCD进行分割,如图1,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分化线可以剪出一副“七巧板”,用这些部件可以拼出很多图案,图2就是用其中6块拼出的“飞机”.若△GOM的面积为1,则“飞机”的面积为 ▲ .
9. 一块矩形木板,它的右上角有一个圆洞,现设想将它改造成火锅餐桌桌面,要求木板大小不变,且使圆洞的圆心在矩形桌面的对角线交点上。木工师傅想到了一个巧妙的办法,他测量了PQ与圆洞的切点K到点B的距离及相关数据(单位:cm)后,从点N沿折线NF-FM(NF∥BC,FM∥AB)切割,如图1所示。图2中的矩形EFGH是切割后的两块木板拼接成符合要求的矩形桌面示意图(不重叠、无缝隙、不计损耗),则CN,AM的长分别是 ▲ .
10. 问题探究
(1)请在图①中作出两条直线,使它们将圆面四等分;
(2)如图②,M是正方形ABCD内一定点,请在图②中作出两条直线(要求其中一条直线必须过点M),使它们将正方形ABCD的面积四等分,并说明理由.
问题解决
(3)如图③,在四边形ABCD中,AB∥CD,AB+CD=BC,点P是AD的中点,如果AB=,CD=,且,那么在边BC上是否存在一点Q,使PQ所在直线将四边形ABCD的面积分成相等的两部分?若存在,求出BQ的长;若不存在,说明理由.
11. 我们知道,矩形是特殊的平行四边形,所以矩形除了具备平行四边形的一切性质还有其特殊的性质;同样,黄金矩形是特殊的矩形,因此黄金矩形有与一般矩形不一样的知识.
已知平行四边形ABCD,∠A=60°,AB=2a,AD=a.
(1)把所给的平行四边形ABCD用两种方式分割并作说明(见题答卡表格里的示例);
要求:用直线段分割,分割成的图形是学习过的特殊图形且不超出四个.
(2)图中关于边、角和对角线会有若干关系或问题.现在请计算两条对角线的长度.
要求:计算对角线BD长的过程中要有必要的论证;直接写出对角线AC的长.
解:在表格中作答
分割图形
分割或图形说明
示例
示例①分割成两个菱形。
②两个菱形的边长都为a,锐角都为60°。
12. 下面给出的正多边形的边长都是20 cm.请分别按下列要求设计一种剪拼方法(用虚线表示你的设计方案,把剪拼线段用粗黑实线,在图中标注出必要的符号和数据,并作简要说明.
(1)将图1中的正方形纸片剪拼成一个底面是正方形的直四棱柱模型,使它的表面积与原正方形面积相等;
(2)将图2中的正三角形纸片剪拼成一个底面是正三角形的直三棱柱模型,使它的表面积与原正三角形的面积相等;
(3)将图3中的正五边形纸片剪拼成一个底面是正五边形的直五棱柱模型,使它的表面积与原正五边形的面积相等.
13. 矩形纸片ABCD中,AB=5,AD=4.
(1)如图1,四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形.你能否在该矩形中裁剪出一个面积最大的正方形,最大面积是多少?说明理由;
(2)请用矩形纸片ABCD剪拼成一个面积最大的正方形.要求:在图2的矩形ABCD中画出裁剪线,并在网格中画出用裁剪出的纸片拼成的正方形示意图(使正方形的顶点都在网格的格点上).
14. 雅安芦山发生7.0级地震后,某校师生准备了一些等腰直角三角形纸片,从每张纸片中剪出一个半圆制作玩具,寄给灾区的小朋友.已知如图,是腰长为4的等腰直角三角形ABC,要求剪出的半圆的直径在△ABC的边上,且半圆的弧与△ABC的其他两边相切,请作出所有不同方案的示意图,并求出相应半圆的半径(结果保留根号).
二、几何体的展开问题:
典型例题:
1.如图是一个长方体包装盒,则它的平面展开图是【 】
A.B.C.D.2.圆锥底面圆的半径为3cm,其侧面展开图是半圆,其圆锥母线长为【 】
A.3cm B.6cm C.9cm D.12cm
一个几何体的三视图如图所示,则该几何体的侧面展开图的面积为【 】
A.6cm2 B.4πcm2 C.6πcm2 D.9πcm2
4. 下列四个图形中,是三棱柱的平面展开图的是【 】
5. 一个圆锥的侧面积是底面积的4倍,则圆锥侧面展开图的扇形的圆心角是【 】
A.60° B.90° C.120° D.180°
6. 已知一个圆柱的侧面展开图为如图所示的矩形,则其底面圆的面积为【 】
A. B. 4 C. 或4 D.2或4
7. 小明为了鼓励芦山地震灾区的学生早日走出阴影,好好学习,制作了一个正方体礼盒(如图).礼盒每个面上各有一个字,连起来组成“芦山学子加油”,其中“芦”的对面是“学”,“加”的对面是“油”,则它的平面展开图可能是【 】
B. C.D.
下列图形中,是圆锥侧面展开图的是【 】
B. C. D.
9. 如图,一个几何体上半部为正四棱椎,下半部为立方体,且有一个面涂有颜色,下列图形中,是该几何体的表面展开图的是【 】
B.
C.D.
10. 已知圆柱的底面半径为3cm,母线长为5cm,则圆柱的侧面积是【 】
A.30cm2 B.30πcm2 C.15cm2 D.15πcm2
如图示一个几何体的三视图,则这个几何体的侧面积是【 】
A.12πcm2 B.8πcm2 C.6πcm2 D.3πcm2
12. 一个立体图形的三视图如图所示,根据图中数据求得这个立体图形的的表面积为【 】
A. B. C. D.
把如图中的三棱柱展开,所得到的展开图是【 】
B.C.D.
14. 一个圆锥的左视图是一个正三角形,则这个圆锥的侧面展开图的圆心角等于【 】
A.60° B.90° C.120° D.180°
15.若圆锥的轴截图为等边三角形,则称此圆锥为正圆锥,则正圆锥的侧面展开图的圆心角是【 】
A.90° B.120° C.150° D.180°
16.已知圆锥底面半径为5cm,高为12cm,则圆锥的侧面展开图的面积是 ▲ .
17.一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图扇形的圆心角是 ▲ .
18.已知圆锥母线长为为5cm,底面半径为3cm,则圆锥的侧面展开图的面积是 ▲ .
19.圆锥的底面半径是1,侧面积是2π,则这个圆锥的侧面展开图的圆心角为 ▲ .
20.圆锥的母线长为6cm,底面周长为5πcm,则圆锥的侧面积为
▲ .
21.高为4,底面半径为3的圆锥,则圆锥的侧面展开图的面积是 ▲ .
22.一圆锥的底面半径为1cm,母线长2cm,则该圆锥的侧面积为 ▲ cm2.
23.已知圆锥的底面周长是10π,其侧面展开后所得扇形的圆心角为90°,则该圆锥的母线长是 ▲ .
24.如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是 ▲ .
25.如图,张老师在上课前用硬纸做了一个无底的圆锥形教具,那么这个教具的用纸面积是
▲ cm2.(不考虑接缝等因素,计算结果用π表示).
26.一个圆锥形零件,高为8cm,底面圆的直径为12cm,则此圆锥的侧面积是 ▲ cm2.
27.如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为
▲ m(容器厚度忽略不计).
28.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 ▲ .
29.底面半径为1,母线长为2的圆锥侧面积为 ▲ .
30.如图,圆锥的侧面展开图是一个半圆,求母线AB与高AO的夹角.参考公式:圆锥的侧面积S=πrl,其中r为底面半径,l为母线长.
三、几何体展开图的折叠问题:
典型例题:
如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“共”字一面的相对面上的字是【 】
美 B.丽 C.家 D.园
将一边长为2的正方形纸片折成四部分,再沿折痕折起来,恰好不能重叠的搭成一个三棱锥,则三棱锥四个面中面积最小的面积是【 】
A.1 B. C. D.
3.如图是一个长方体形状包装盒的表面展开图.折叠制作完成后得到长方体的容积是(包装材料厚度不计)【 】
A.40×40×70 B.70×70×80 C.80×80×80 D.40×70×80
一个正方体的平面展开图如图所示,将它折成正方体后,与汉字“岳”相对的面上的汉字是【 】
建 B.设 C.和 D.谐
5. 用如图所示的扇形纸片制作一个圆锥的侧面,要求圆锥的高是4 cm,底面周长是6π cm,则扇形的半径为【 】
A.3cm B.5cm C.6cm D.8cm
下列图形中,能通过折叠围成一个三棱柱的是【 】
B.C.D.
如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是【 】
大 B.伟 C.国 D.的
8. 用一圆心角为120°,半径为6cm的扇形做成一个圆锥的侧面,这个圆锥的底面的半径是【 】
A.1cm B.2cm C.3cm D.4cm
9. 用半径为3cm,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为【 】
A. B.1.5cm C. D.1cm
10. 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是【 】
美 B.丽 C.云 D.南
10. 下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方形包装盒的是【 】
A.B.C.D.
下列各图形中,经过折叠能围成一个立方体的是【 】
B. C. D.
12. 如图是正方形的一种张开图,其中每个面上都标有一个数字。那么在原正方形中,与数字“2”相对的面上的数字是【 】
(A)1 (B)4 (C)5 (D)6
13. 如图,一扇形纸片,圆心角∠AOB为120°,弦AB的长为cm,用它围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为 ▲ .
14.将半径为4cm的半圆围成一个圆锥,这个圆锥的高为 ▲ cm.
15. 如图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“香”相对的面上的汉字是 ▲ .
16. 用半径为10cm,圆心角为216°的扇形做成一个圆锥的侧面,则这个圆锥的高为
▲ cm.
17. 用一个圆心角为90°,半径为32cm的扇形作为一个圆锥的侧面(接缝处不重叠),则这个圆锥的底面圆的半径为 ▲ cm.
18. 已知一个扇形的半径为60cm,圆心角为150°,用它围成一个圆锥的侧面,那么圆锥的底面半径为 ▲ cm.
19.用一个圆心角为120°,半径为4的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径为 ▲ cm.
20. 如图,如果从半径为5cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高是 ▲ cm.
21. 如图,从半径为9cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为 ▲ cm.
22. 以下三组图形都是由四个等边三角形组成.能折成多面体的选项序号是 ▲ .
23. 如图,从直径为4cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是 ▲ cm.
同课章节目录
