第十八章平行四边形单元练习 含答案 2022—2023学年人教版数学八年级下册
文档属性
| 名称 | 第十八章平行四边形单元练习 含答案 2022—2023学年人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 472.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 16:22:32 | ||
图片预览

文档简介
第十八章平行四边形 单元练习
一、单选题
1.平行四边形ABCD中,若比小40°,则的度数为( ).
A.60° B.70° C.80° D.110°
2.已知平行四边形ABCD中,∠B=5∠A,则∠C=( )
A.30° B.60° C.120° D.150°
3.如图,在平行四边形ABCD中,对角线AC,BD相交于O,AC=10cm,AB=4cm,BD⊥AB,则BD的长为( )
A.4cm B..5cm C.6cm D..8cm
4.四边形ABCD的两条对角线AC、BD互相平分.添加下列条件,一定能判定四边形ABCD为菱形的是( )
A.∠ABD=∠BDC B.∠ABD=∠BAC C.∠ABD=∠CBD D.∠ABD=∠BCA
5.已知的周长为,,,分别为,,的中点,且,,那么的长是( )
A. B. C. D.
6.下列命题中,真命题是( )
A.对角线互相垂直的四边形是菱形
B.对角线互相垂直平分的四边形是正方形
C.四条边相等的四边形是矩形
D.有一组对边平行且相等的四边形是平行四边形
7.如图,菱形ABCD的周长是4cm,∠ABC=60°,那么这个菱形的对角线AC的长是( )
A.1cm B.2 cm C.3cm D.4cm
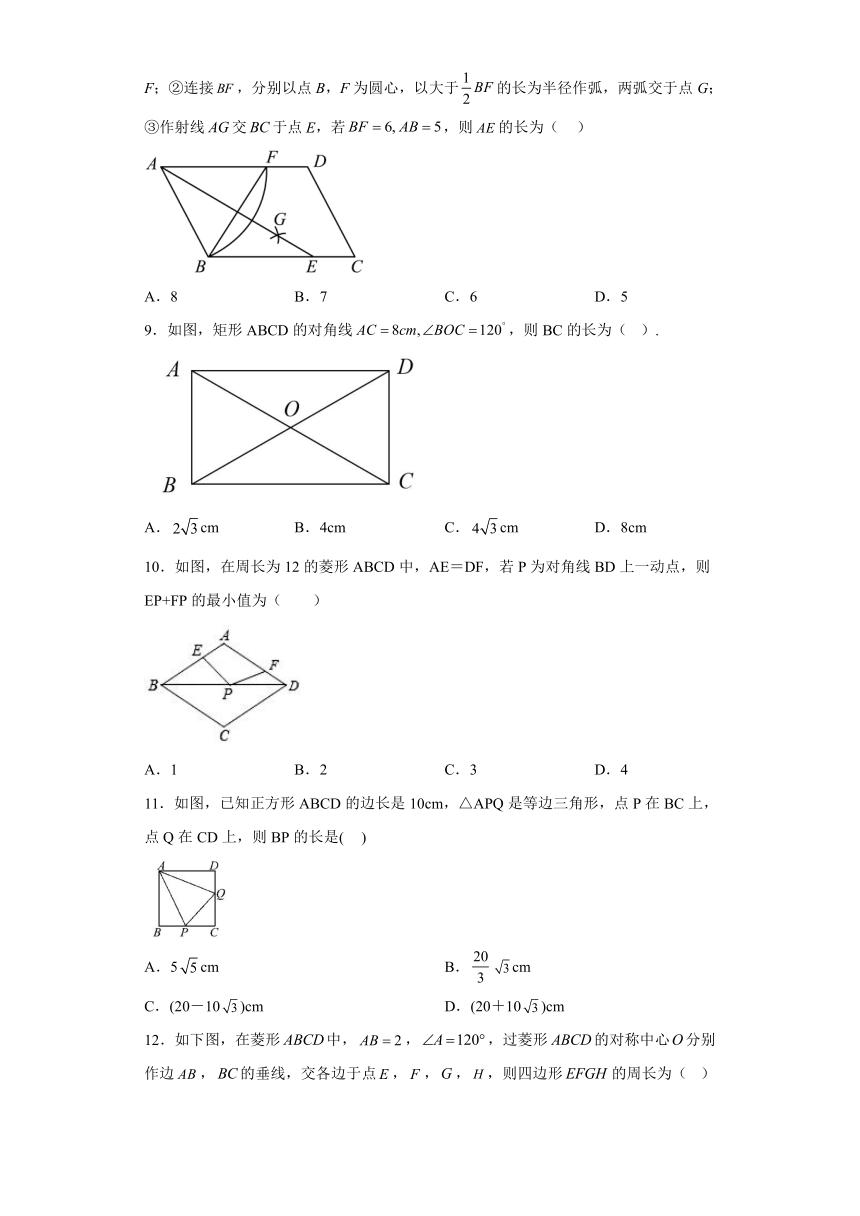
8.如图3,在中,按如下步骤作图:①以A为圆心,长为半径画弧交于F;②连接,分别以点B,F为圆心,以大于的长为半径作弧,两弧交于点G;③作射线交于点E,若,则的长为( )
A.8 B.7 C.6 D.5
9.如图,矩形ABCD的对角线,则BC的长为( ).
A.cm B.4cm C.cm D.8cm
10.如图,在周长为12的菱形ABCD中,AE=DF,若P为对角线BD上一动点,则EP+FP的最小值为( )
A.1 B.2 C.3 D.4
11.如图,已知正方形ABCD的边长是10cm,△APQ是等边三角形,点P在BC上,点Q在CD上,则BP的长是( )
A.5cm B.cm
C.(20-10)cm D.(20+10)cm
12.如下图,在菱形中,,,过菱形的对称中心分别作边,的垂线,交各边于点,,,,则四边形的周长为( )
A. B. C. D.
二、填空题
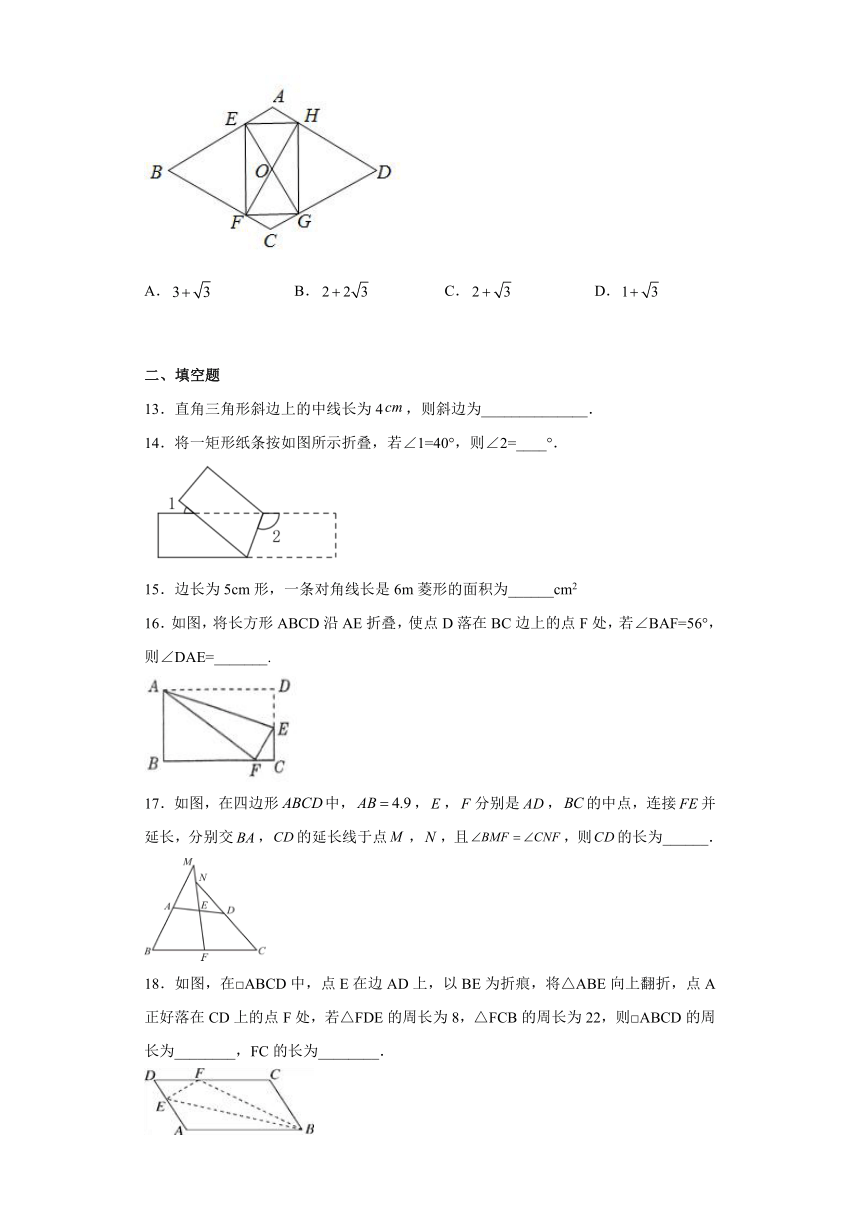
13.直角三角形斜边上的中线长为4,则斜边为______________.
14.将一矩形纸条按如图所示折叠,若∠1=40°,则∠2=____°.
15.边长为5cm形,一条对角线长是6m菱形的面积为______cm2
16.如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F处,若∠BAF=56°,则∠DAE=_______.
17.如图,在四边形中,,,分别是,的中点,连接并延长,分别交,的延长线于点,,且,则的长为______.
18.如图,在□ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F处,若△FDE的周长为8,△FCB的周长为22,则□ABCD的周长为________,FC的长为________.
三、解答题
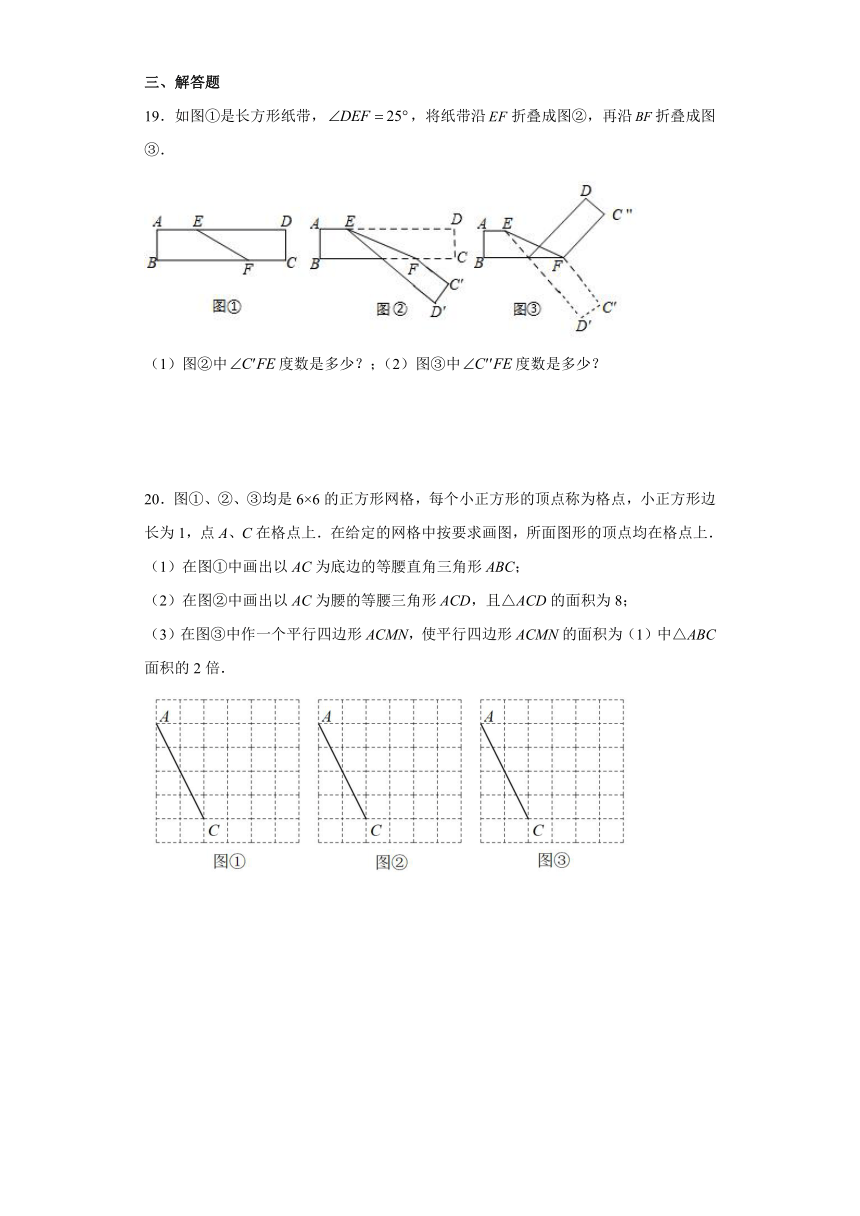
19.如图①是长方形纸带,,将纸带沿折叠成图②,再沿折叠成图③.
(1)图②中度数是多少?;(2)图③中度数是多少?
20.图①、②、③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形边长为1,点A、C在格点上.在给定的网格中按要求画图,所面图形的顶点均在格点上.
(1)在图①中画出以AC为底边的等腰直角三角形ABC;
(2)在图②中画出以AC为腰的等腰三角形ACD,且△ACD的面积为8;
(3)在图③中作一个平行四边形ACMN,使平行四边形ACMN的面积为(1)中△ABC面积的2倍.
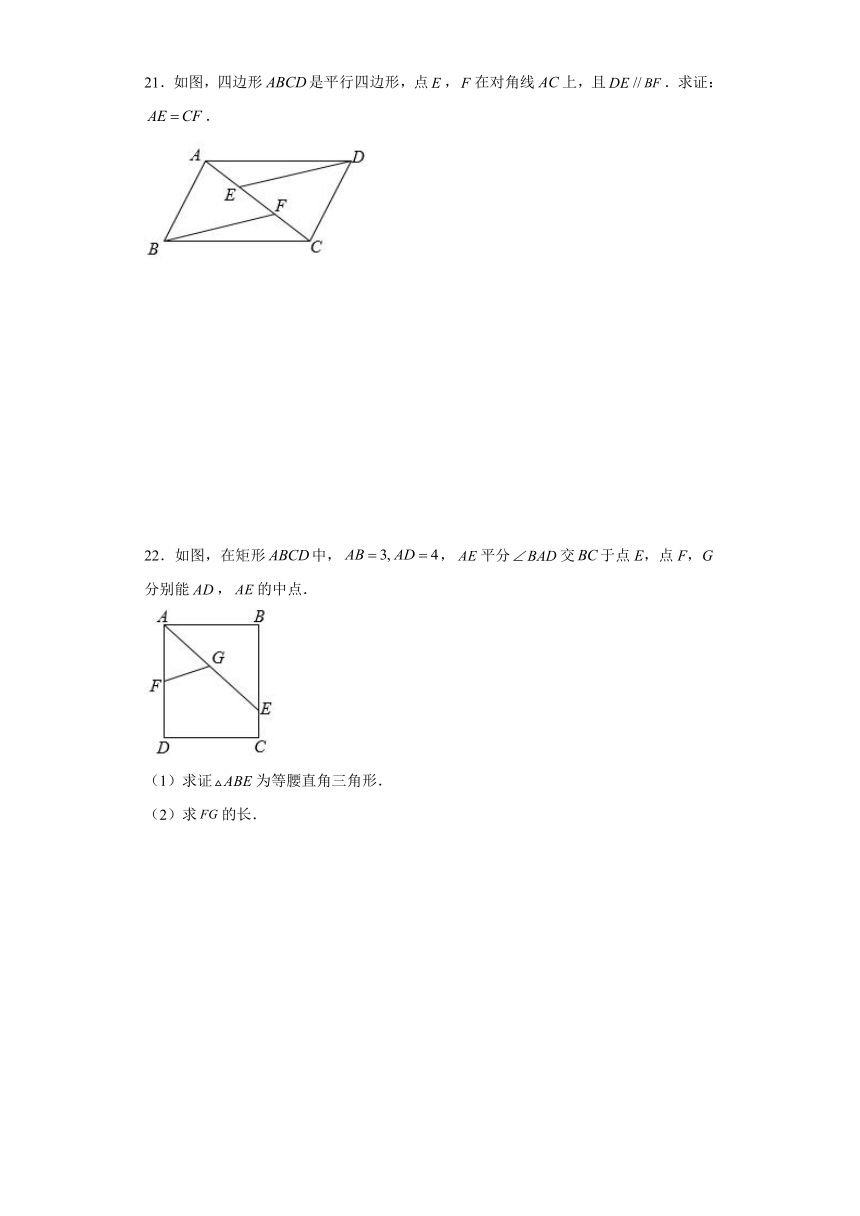
21.如图,四边形是平行四边形,点,在对角线上,且//.求证:.
22.如图,在矩形中,,平分交于点E,点F,G分别能,的中点.
(1)求证为等腰直角三角形.
(2)求的长.
23.如图,在中,,于点,平分,分别交、于点、,于点,连接,求证:四边形是菱形.
24.如图,E,F分别是矩形ABCD的边AB,AD上的点,∠FEC=∠FCE=45°.
(1)求证:AE=DF;
(2)若AD= 6,EFC的面积为10,求线段BE的长.
参考答案
1.B
2.A
3.C
4.C
5.B
6.D
7.A
8.A
9.C
10.C
11.C
12.A
13.8
14.110
15.24
16.17°
17.
18. 30 7
19.解:(1)长方形的对边是平行的,
;
图②中的,
(2)图②中,,
图③中,.
20.(1)由题意可得,AC=,,AB=BC=如图①所示:△ABC即为所求;
(2)AC可以看作是以其为斜边,直角边分别为2、4的直角三角形,以过点C的直角边为对称轴作其对称图形即可,底边为4,高为4,面积为8,如图②所示:△ACD即为所求;
(3)利用图①中的图形作其中心对称图形即可,如图③所示:平行四边形ACMN即为所求.
21.∵四边形是平行四边形,
∴,
且,
∴,
∵,
∴,
又∵,,
∴,
∵在与中:
∴,
所以.
22.解:(1)∵四边形ABCD是矩形,
∴∠BAD=∠B=∠C=90°,AB=CD=3,AD=BC=4,AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠DAE=∠BAE=45°,
∴∠BAE=∠AEB=45°,
∴△ABE为等腰直角三角形;
(2)连接DE,如图所示:
∵△ABE为等腰直角三角形,
∴AB=BE=3,
∴EC=BC-BE=1,
∴DE=,
∵点F、G分别为AD、AE的中点,
∴FG是△ADE的中位线,
∴FG=DE=.
23.证明:∵∠ACB=90°,AE平分∠BAC,EH⊥AB,
∴CE=EH,
在Rt△ACE和Rt△AHE中,AE=AE,CE=EH,由勾股定理得:AC=AH,
∵AE平分∠CAB,
∴∠CAF=∠HAF,
在△CAF和△HAF中
∴△CAF≌△HAF(SAS),
∴∠ACD=∠AHF,
∵CD⊥AB,∠ACB=90°,
∴∠CDA=∠ACB=90°,
∴∠B+∠CAB=90°,∠CAB+∠ACD=90°,
∴∠ACD=∠B=∠AHF,
∴FHCE,
∵CD⊥AB,EH⊥AB,
∴CFEH,
∴四边形CFHE是平行四边形,
∵CE=EH,
∴四边形CFHE是菱形.
24. (1)
证明:∵四边形ABCD是矩形
∴∠A=D=90°
∴∠AEF+∠AFE=90°
∵∠FEC=∠FCE=45°
∴EF=CF,∠EFC=180°-(∠FEC+∠FCE)=90°
∴∠AFE+∠CFD=180°-∠EFC=90°
∴∠AEF=∠CFD
在△AEF和△DFC中,
∴△AEF≌△DFC(AAS)
∴AE=DF
(2)
解:∵四边形ABCD是矩形,AD=6
∴BC=AD=6,∠B=90°
由(1)可知∠EFC=90°,EF=CF
∴△EFC的面积=
∵△EFC的面积为10
∴
∴
∴
在Rt△EFC中,∠EFC=90°
∴
在Rt△BCE中,∠B=90°
∴
一、单选题
1.平行四边形ABCD中,若比小40°,则的度数为( ).
A.60° B.70° C.80° D.110°
2.已知平行四边形ABCD中,∠B=5∠A,则∠C=( )
A.30° B.60° C.120° D.150°
3.如图,在平行四边形ABCD中,对角线AC,BD相交于O,AC=10cm,AB=4cm,BD⊥AB,则BD的长为( )
A.4cm B..5cm C.6cm D..8cm
4.四边形ABCD的两条对角线AC、BD互相平分.添加下列条件,一定能判定四边形ABCD为菱形的是( )
A.∠ABD=∠BDC B.∠ABD=∠BAC C.∠ABD=∠CBD D.∠ABD=∠BCA
5.已知的周长为,,,分别为,,的中点,且,,那么的长是( )
A. B. C. D.
6.下列命题中,真命题是( )
A.对角线互相垂直的四边形是菱形
B.对角线互相垂直平分的四边形是正方形
C.四条边相等的四边形是矩形
D.有一组对边平行且相等的四边形是平行四边形
7.如图,菱形ABCD的周长是4cm,∠ABC=60°,那么这个菱形的对角线AC的长是( )
A.1cm B.2 cm C.3cm D.4cm
8.如图3,在中,按如下步骤作图:①以A为圆心,长为半径画弧交于F;②连接,分别以点B,F为圆心,以大于的长为半径作弧,两弧交于点G;③作射线交于点E,若,则的长为( )
A.8 B.7 C.6 D.5
9.如图,矩形ABCD的对角线,则BC的长为( ).
A.cm B.4cm C.cm D.8cm
10.如图,在周长为12的菱形ABCD中,AE=DF,若P为对角线BD上一动点,则EP+FP的最小值为( )
A.1 B.2 C.3 D.4
11.如图,已知正方形ABCD的边长是10cm,△APQ是等边三角形,点P在BC上,点Q在CD上,则BP的长是( )
A.5cm B.cm
C.(20-10)cm D.(20+10)cm
12.如下图,在菱形中,,,过菱形的对称中心分别作边,的垂线,交各边于点,,,,则四边形的周长为( )
A. B. C. D.
二、填空题
13.直角三角形斜边上的中线长为4,则斜边为______________.
14.将一矩形纸条按如图所示折叠,若∠1=40°,则∠2=____°.
15.边长为5cm形,一条对角线长是6m菱形的面积为______cm2
16.如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F处,若∠BAF=56°,则∠DAE=_______.
17.如图,在四边形中,,,分别是,的中点,连接并延长,分别交,的延长线于点,,且,则的长为______.
18.如图,在□ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F处,若△FDE的周长为8,△FCB的周长为22,则□ABCD的周长为________,FC的长为________.
三、解答题
19.如图①是长方形纸带,,将纸带沿折叠成图②,再沿折叠成图③.
(1)图②中度数是多少?;(2)图③中度数是多少?
20.图①、②、③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形边长为1,点A、C在格点上.在给定的网格中按要求画图,所面图形的顶点均在格点上.
(1)在图①中画出以AC为底边的等腰直角三角形ABC;
(2)在图②中画出以AC为腰的等腰三角形ACD,且△ACD的面积为8;
(3)在图③中作一个平行四边形ACMN,使平行四边形ACMN的面积为(1)中△ABC面积的2倍.
21.如图,四边形是平行四边形,点,在对角线上,且//.求证:.
22.如图,在矩形中,,平分交于点E,点F,G分别能,的中点.
(1)求证为等腰直角三角形.
(2)求的长.
23.如图,在中,,于点,平分,分别交、于点、,于点,连接,求证:四边形是菱形.
24.如图,E,F分别是矩形ABCD的边AB,AD上的点,∠FEC=∠FCE=45°.
(1)求证:AE=DF;
(2)若AD= 6,EFC的面积为10,求线段BE的长.
参考答案
1.B
2.A
3.C
4.C
5.B
6.D
7.A
8.A
9.C
10.C
11.C
12.A
13.8
14.110
15.24
16.17°
17.
18. 30 7
19.解:(1)长方形的对边是平行的,
;
图②中的,
(2)图②中,,
图③中,.
20.(1)由题意可得,AC=,,AB=BC=如图①所示:△ABC即为所求;
(2)AC可以看作是以其为斜边,直角边分别为2、4的直角三角形,以过点C的直角边为对称轴作其对称图形即可,底边为4,高为4,面积为8,如图②所示:△ACD即为所求;
(3)利用图①中的图形作其中心对称图形即可,如图③所示:平行四边形ACMN即为所求.
21.∵四边形是平行四边形,
∴,
且,
∴,
∵,
∴,
又∵,,
∴,
∵在与中:
∴,
所以.
22.解:(1)∵四边形ABCD是矩形,
∴∠BAD=∠B=∠C=90°,AB=CD=3,AD=BC=4,AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠DAE=∠BAE=45°,
∴∠BAE=∠AEB=45°,
∴△ABE为等腰直角三角形;
(2)连接DE,如图所示:
∵△ABE为等腰直角三角形,
∴AB=BE=3,
∴EC=BC-BE=1,
∴DE=,
∵点F、G分别为AD、AE的中点,
∴FG是△ADE的中位线,
∴FG=DE=.
23.证明:∵∠ACB=90°,AE平分∠BAC,EH⊥AB,
∴CE=EH,
在Rt△ACE和Rt△AHE中,AE=AE,CE=EH,由勾股定理得:AC=AH,
∵AE平分∠CAB,
∴∠CAF=∠HAF,
在△CAF和△HAF中
∴△CAF≌△HAF(SAS),
∴∠ACD=∠AHF,
∵CD⊥AB,∠ACB=90°,
∴∠CDA=∠ACB=90°,
∴∠B+∠CAB=90°,∠CAB+∠ACD=90°,
∴∠ACD=∠B=∠AHF,
∴FHCE,
∵CD⊥AB,EH⊥AB,
∴CFEH,
∴四边形CFHE是平行四边形,
∵CE=EH,
∴四边形CFHE是菱形.
24. (1)
证明:∵四边形ABCD是矩形
∴∠A=D=90°
∴∠AEF+∠AFE=90°
∵∠FEC=∠FCE=45°
∴EF=CF,∠EFC=180°-(∠FEC+∠FCE)=90°
∴∠AFE+∠CFD=180°-∠EFC=90°
∴∠AEF=∠CFD
在△AEF和△DFC中,
∴△AEF≌△DFC(AAS)
∴AE=DF
(2)
解:∵四边形ABCD是矩形,AD=6
∴BC=AD=6,∠B=90°
由(1)可知∠EFC=90°,EF=CF
∴△EFC的面积=
∵△EFC的面积为10
∴
∴
∴
在Rt△EFC中,∠EFC=90°
∴
在Rt△BCE中,∠B=90°
∴
