2022--2023学年北师大版七年级数学下册第5章 生活中的轴对称强化训练(无答案)
文档属性
| 名称 | 2022--2023学年北师大版七年级数学下册第5章 生活中的轴对称强化训练(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 535.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 00:00:00 | ||
图片预览



文档简介
第5章 生活中的轴对称(强化训练)-北师大版七年级下册
一.选择题
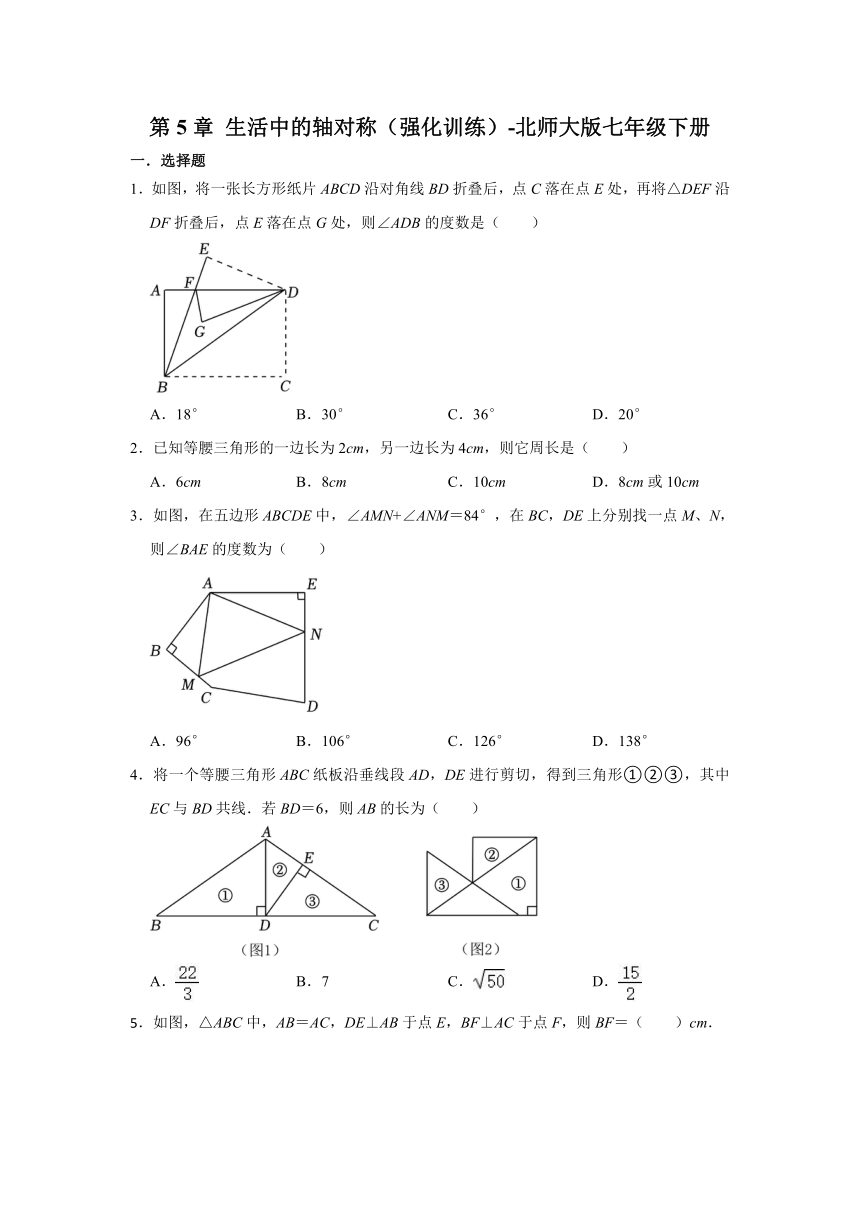
1.如图,将一张长方形纸片ABCD沿对角线BD折叠后,点C落在点E处,再将△DEF沿DF折叠后,点E落在点G处,则∠ADB的度数是( )
A.18° B.30° C.36° D.20°
2.已知等腰三角形的一边长为2cm,另一边长为4cm,则它周长是( )
A.6cm B.8cm C.10cm D.8cm或10cm
3.如图,在五边形ABCDE中,∠AMN+∠ANM=84°,在BC,DE上分别找一点M、N,则∠BAE的度数为( )
A.96° B.106° C.126° D.138°
4.将一个等腰三角形ABC纸板沿垂线段AD,DE进行剪切,得到三角形①②③,其中EC与BD共线.若BD=6,则AB的长为( )
A. B.7 C. D.
.如图,△ABC中,AB=AC,DE⊥AB于点E,BF⊥AC于点F,则BF=( )cm.
A.4.8 B.6 C.5 D.6.4
.“松风树人”,美丽的松中是我们可爱的校园,人人都很喜爱它,是轴对称图形的汉字是( )
A. B. C. D.
.如图,在四边形ABCD中,∠ABC=60°,∠BCD>∠CBD,BC=24,P,BC上的动点,当CP+PQ取得最小值时( )
A.8 B.10 C.12 D.16
.如图,在等边△PQB中,点A为PQ上一动点(不与P,Q重合),连接PC.有以下结论:①PB平分∠ABC;②AQ=CP;④PB=PA+PC;⑤当BC⊥BQ时( )
A.①②③ B.②③④ C.③④⑤ D.②③④⑤
.如图,线段AB,BC的垂直平分线l1、l2相交于点O.若∠OEB=46°,则∠AOC=( )
A.92° B.88° C.46° D.86°
.如图,点A,A1,A2,A3,…在同一直线上,AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4,…,若∠B的度数为x,则∠AnBnAn+1的度数为( )
A. B.
C. D.
二.填空题
.如图,在△ABC中,∠C=90°,若S△ABD=22cm2,AB=10cm,则CD为 cm.
.如图,DP所在直线是BC的垂直平分线,垂足为点P,若∠BAC=80°,则∠BDC= .
.如图,在△ABC中,AB=AC=BC=2,CE是△ABC的两条中线,
(1)∠BAD= °;
(2)P点是线段AD上一个动点,则BP+EP的最小值是 .
.如图,∠AOB=30°,点D为∠AOB平分线OC上一点,OB分别于点P,Q,点E是OA上异于点P的一点,则△ODE的面积为 .
.如图,△ABC是等边三角形,将按如图的方式进行折叠,折痕分别与AB、BC交于点D、E,下列四个结论:①∠FDE+∠FED=120°;③AD=EC;④若AF=1,O是折痕DE上一动点,则OF+OC的最小值是4 .
三.解答题
.如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)(3,4).
(1)若△A1B1C1与△ABC关于y轴成轴对称,请在网格中画出△A1B1C1,并写出△A1B1C1三顶点坐标:A1 ,B1 ,C1 ;
(2)计算△ABC的面积;
(3)若点P为x轴上一点,使PA+PB最小(保留作图痕迹).
.如图,在△ABC中,AD⊥BC,BD=CD,延长BC至E,连接AE.
(1)若∠E=24°,求∠B;
(2)若AB=5,AD=4,求△ABE面积.
.如图,A(﹣4,3),B(4,3),C(1,﹣1)都是格点,且BC=5,并保留作图痕迹(画图过程用虚线,画图结果用实线表示).
(1)在图1中作△ABC的中线CE与BD,设CE与BD交于点F;
(2)在图2中,在y轴上找点Q,使得AQ+GQ最小;
(3)在图3中的AB上找一点M,使∠BCM=∠GCM;
(4)在图3中作点N(2,3)关于CM的对称点Q.
.如图11,在△ABC中,AB=AC,点P是BC边上一点,∠BAP=α(30°<α<50°),连接BD交AP于点G.连接DC并延长交直线AP于点E,连接BE、AD.
(1)当α=40°时,∠AEB= ;
(2)嘉琪说:“无需给出α(30°<α<50°)的具体数值,也可求出∠AEB的值.”请运用相关知识验证嘉琪的说法是否正确.
.如图,在△ABC中,AB=AC,作点C关于直线l的对称点M,连接AM、BM
(1)依题意补全图形;
(2)连接CN,求证:∠ACN=∠ABM;
(3)过点A作AH⊥BM于点H,用等式表示线段BN、2NH、MN之间的数量关系,并证明.
一.选择题
1.如图,将一张长方形纸片ABCD沿对角线BD折叠后,点C落在点E处,再将△DEF沿DF折叠后,点E落在点G处,则∠ADB的度数是( )
A.18° B.30° C.36° D.20°
2.已知等腰三角形的一边长为2cm,另一边长为4cm,则它周长是( )
A.6cm B.8cm C.10cm D.8cm或10cm
3.如图,在五边形ABCDE中,∠AMN+∠ANM=84°,在BC,DE上分别找一点M、N,则∠BAE的度数为( )
A.96° B.106° C.126° D.138°
4.将一个等腰三角形ABC纸板沿垂线段AD,DE进行剪切,得到三角形①②③,其中EC与BD共线.若BD=6,则AB的长为( )
A. B.7 C. D.
.如图,△ABC中,AB=AC,DE⊥AB于点E,BF⊥AC于点F,则BF=( )cm.
A.4.8 B.6 C.5 D.6.4
.“松风树人”,美丽的松中是我们可爱的校园,人人都很喜爱它,是轴对称图形的汉字是( )
A. B. C. D.
.如图,在四边形ABCD中,∠ABC=60°,∠BCD>∠CBD,BC=24,P,BC上的动点,当CP+PQ取得最小值时( )
A.8 B.10 C.12 D.16
.如图,在等边△PQB中,点A为PQ上一动点(不与P,Q重合),连接PC.有以下结论:①PB平分∠ABC;②AQ=CP;④PB=PA+PC;⑤当BC⊥BQ时( )
A.①②③ B.②③④ C.③④⑤ D.②③④⑤
.如图,线段AB,BC的垂直平分线l1、l2相交于点O.若∠OEB=46°,则∠AOC=( )
A.92° B.88° C.46° D.86°
.如图,点A,A1,A2,A3,…在同一直线上,AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4,…,若∠B的度数为x,则∠AnBnAn+1的度数为( )
A. B.
C. D.
二.填空题
.如图,在△ABC中,∠C=90°,若S△ABD=22cm2,AB=10cm,则CD为 cm.
.如图,DP所在直线是BC的垂直平分线,垂足为点P,若∠BAC=80°,则∠BDC= .
.如图,在△ABC中,AB=AC=BC=2,CE是△ABC的两条中线,
(1)∠BAD= °;
(2)P点是线段AD上一个动点,则BP+EP的最小值是 .
.如图,∠AOB=30°,点D为∠AOB平分线OC上一点,OB分别于点P,Q,点E是OA上异于点P的一点,则△ODE的面积为 .
.如图,△ABC是等边三角形,将按如图的方式进行折叠,折痕分别与AB、BC交于点D、E,下列四个结论:①∠FDE+∠FED=120°;③AD=EC;④若AF=1,O是折痕DE上一动点,则OF+OC的最小值是4 .
三.解答题
.如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)(3,4).
(1)若△A1B1C1与△ABC关于y轴成轴对称,请在网格中画出△A1B1C1,并写出△A1B1C1三顶点坐标:A1 ,B1 ,C1 ;
(2)计算△ABC的面积;
(3)若点P为x轴上一点,使PA+PB最小(保留作图痕迹).
.如图,在△ABC中,AD⊥BC,BD=CD,延长BC至E,连接AE.
(1)若∠E=24°,求∠B;
(2)若AB=5,AD=4,求△ABE面积.
.如图,A(﹣4,3),B(4,3),C(1,﹣1)都是格点,且BC=5,并保留作图痕迹(画图过程用虚线,画图结果用实线表示).
(1)在图1中作△ABC的中线CE与BD,设CE与BD交于点F;
(2)在图2中,在y轴上找点Q,使得AQ+GQ最小;
(3)在图3中的AB上找一点M,使∠BCM=∠GCM;
(4)在图3中作点N(2,3)关于CM的对称点Q.
.如图11,在△ABC中,AB=AC,点P是BC边上一点,∠BAP=α(30°<α<50°),连接BD交AP于点G.连接DC并延长交直线AP于点E,连接BE、AD.
(1)当α=40°时,∠AEB= ;
(2)嘉琪说:“无需给出α(30°<α<50°)的具体数值,也可求出∠AEB的值.”请运用相关知识验证嘉琪的说法是否正确.
.如图,在△ABC中,AB=AC,作点C关于直线l的对称点M,连接AM、BM
(1)依题意补全图形;
(2)连接CN,求证:∠ACN=∠ABM;
(3)过点A作AH⊥BM于点H,用等式表示线段BN、2NH、MN之间的数量关系,并证明.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
