2022--2023学年人教版七年级数学下册9.2 一元一次不等式 同步练习(含答案)
文档属性
| 名称 | 2022--2023学年人教版七年级数学下册9.2 一元一次不等式 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 210.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 16:33:06 | ||
图片预览



文档简介
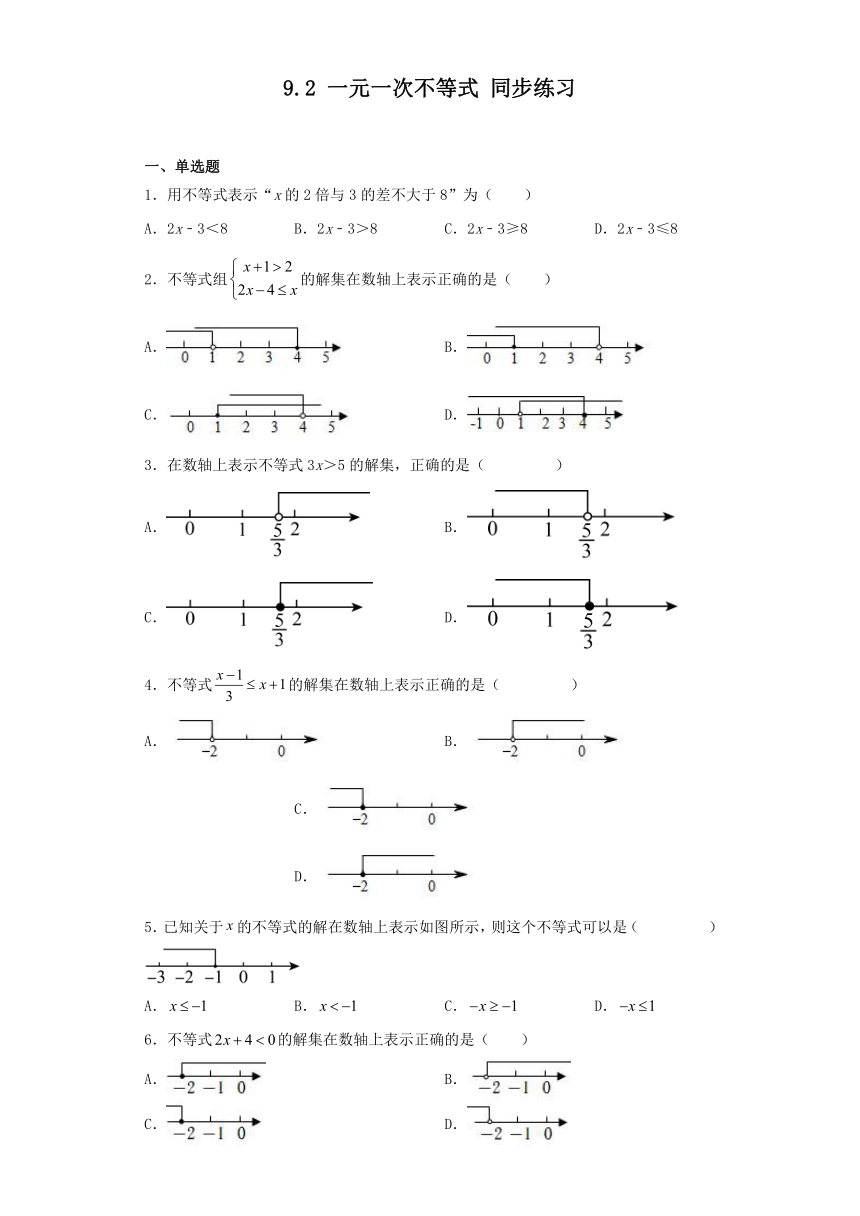
9.2 一元一次不等式 同步练习
一、单选题
1.用不等式表示“x的2倍与3的差不大于8”为( )
A.2x﹣3<8 B.2x﹣3>8 C.2x﹣3≥8 D.2x﹣3≤8
2.不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
3.在数轴上表示不等式3x>5的解集,正确的是( )
A. B.
C. D.
4.不等式的解集在数轴上表示正确的是( )
A. B. C. D.
5.已知关于的不等式的解在数轴上表示如图所示,则这个不等式可以是( )
A. B. C. D.
6.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
7.x与y的差的5倍与2的和是一个非负数,可表示为( )
A.5(x-y)+2>0
B.5(x-y)+2≥0
C.x-5y+2≥0
D.5x-2y+2≤0
8.一次学校智力竞赛中共有道题,规定答对一题得分,答错或不答一道题扣分,得分为分以上可以获得奖品,小锋在本次竞赛中获得了奖品.假设小锋答对了题,可根据题意列出不等式( )
A. B.
C. D.
9.不等式ax-2<0的解集在数轴上表示如图,那么a的取值范围是( )
A. B. C. D.
10.不等式x-2≤0的解集在数轴上表示正确的是( )
A. B.
C. D.
二、填空题
11.不等式的解集是________.
12.不等式的正整数解为___________.
13.我们知道,那么的整数部分就是.如果为的整数部分,且关于的不等式只有个负整数解,则实数的取值范围是_________.
14.不等式3x-6≤2(x-1)的正整数解的和为_______.
15.若关于的方程的解是正数,则的取值范围为__________.
三、解答题
16.大学生小李自主创业,春节期间购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
型号 进价(元/只) 售价(元/只)
A型 10 12
B型 15 23
要使销售文具所获利润不超过进货价格的40%,求至少要购进多少只A型文具?
17.为了提高学生的保护环境意识,某校学生会利用课余时间,组织七、八年级共50名同学参加环保活动,七年级学生平均每人收集10个废弃塑料瓶,八年级学生平均每人收集20个废弃塑料瓶.若所收集的塑料瓶总数不少于800个,至少有多少名八年级学生参加活动?
18.对于任意实数,,定义关于“”的一种运算如下:,例如:,.
(1)若,求的值;
(2)若,求的取值范围.
19.解不等式:>x﹣1.
20.为响应国家“垃圾分类”的号召,温州市开始实施《城镇垃圾分类标准》,某商场向厂家订购了A、B两款垃圾桶工100个,已知购买A款垃圾桶个数不超过30个时,每个A款垃圾桶进价为80元,每增加1个垃圾桶,则该款垃圾桶每个进价减少2元,每个A款垃圾桶进价不低于50元.每个B款垃圾桶的进价为40元,设所购买A款垃圾桶的个数为个.
(1)根据信息填表:
款式 数量(个) 进价(元/个)
A (不超过30个时) 80
(超过30个时) ______
B ______ 40
(2)若订购的垃圾桶的总进价为4800元,则该商场订购了多少个A款垃圾桶?
参考答案
1.D
2.D
3.A
4.D
5.A
6.D
7.B
8.D
9.D
10.B
11.
12.1,2,3
13.
14.10
15.
16. 【详解】解:设购进A型玩具x只, 依题意得:(12﹣10)x+(23﹣15)(100﹣x)≤40%[10x+15(100﹣x)]
解得,x≥50.
答:至少要购进50只A型文具
17.【详解】解:设有x名八年级学生参加活动,
根据题意,得10(50-x)+20x≥800
解得 x≥30
答:至少有30名八年级学生参加活动.
18.(1)
解:任意实数,,定义关于“”的一种运算如下:,
,
,
∴
∴
(2)
解:,
∴,
∴.
19.【详解】解:>x﹣1,
1+2x>3x﹣3,
2x﹣3x>﹣3﹣1,
﹣x>﹣4,
x<4.
20.【详解】解:(1)当>30时,购买A款垃圾桶个数80-2(-30)=140-2,
∵每个A款垃圾桶进价不低于50元
140-2≥50,
解得≤45
∴当45≥>30时,进价为(140-2)元,
∵某商场向厂家订购了A,B两款垃圾桶工100个,
∴B款垃圾桶个数为(100-)个
根据信息填表如下:
款式 数量(个) 进价(元/个)
A (不超过30个时) 80
(超过30个时)
B 40
故答案为140-2,100-;
(2)①当时,A进价为80元/个,
,
解得,符合题意;
②当45≥>30时,A进价为()元/个,
,
解得,(舍去),
答:商场订购了A款垃圾桶20个或40个.
一、单选题
1.用不等式表示“x的2倍与3的差不大于8”为( )
A.2x﹣3<8 B.2x﹣3>8 C.2x﹣3≥8 D.2x﹣3≤8
2.不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
3.在数轴上表示不等式3x>5的解集,正确的是( )
A. B.
C. D.
4.不等式的解集在数轴上表示正确的是( )
A. B. C. D.
5.已知关于的不等式的解在数轴上表示如图所示,则这个不等式可以是( )
A. B. C. D.
6.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
7.x与y的差的5倍与2的和是一个非负数,可表示为( )
A.5(x-y)+2>0
B.5(x-y)+2≥0
C.x-5y+2≥0
D.5x-2y+2≤0
8.一次学校智力竞赛中共有道题,规定答对一题得分,答错或不答一道题扣分,得分为分以上可以获得奖品,小锋在本次竞赛中获得了奖品.假设小锋答对了题,可根据题意列出不等式( )
A. B.
C. D.
9.不等式ax-2<0的解集在数轴上表示如图,那么a的取值范围是( )
A. B. C. D.
10.不等式x-2≤0的解集在数轴上表示正确的是( )
A. B.
C. D.
二、填空题
11.不等式的解集是________.
12.不等式的正整数解为___________.
13.我们知道,那么的整数部分就是.如果为的整数部分,且关于的不等式只有个负整数解,则实数的取值范围是_________.
14.不等式3x-6≤2(x-1)的正整数解的和为_______.
15.若关于的方程的解是正数,则的取值范围为__________.
三、解答题
16.大学生小李自主创业,春节期间购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
型号 进价(元/只) 售价(元/只)
A型 10 12
B型 15 23
要使销售文具所获利润不超过进货价格的40%,求至少要购进多少只A型文具?
17.为了提高学生的保护环境意识,某校学生会利用课余时间,组织七、八年级共50名同学参加环保活动,七年级学生平均每人收集10个废弃塑料瓶,八年级学生平均每人收集20个废弃塑料瓶.若所收集的塑料瓶总数不少于800个,至少有多少名八年级学生参加活动?
18.对于任意实数,,定义关于“”的一种运算如下:,例如:,.
(1)若,求的值;
(2)若,求的取值范围.
19.解不等式:>x﹣1.
20.为响应国家“垃圾分类”的号召,温州市开始实施《城镇垃圾分类标准》,某商场向厂家订购了A、B两款垃圾桶工100个,已知购买A款垃圾桶个数不超过30个时,每个A款垃圾桶进价为80元,每增加1个垃圾桶,则该款垃圾桶每个进价减少2元,每个A款垃圾桶进价不低于50元.每个B款垃圾桶的进价为40元,设所购买A款垃圾桶的个数为个.
(1)根据信息填表:
款式 数量(个) 进价(元/个)
A (不超过30个时) 80
(超过30个时) ______
B ______ 40
(2)若订购的垃圾桶的总进价为4800元,则该商场订购了多少个A款垃圾桶?
参考答案
1.D
2.D
3.A
4.D
5.A
6.D
7.B
8.D
9.D
10.B
11.
12.1,2,3
13.
14.10
15.
16. 【详解】解:设购进A型玩具x只, 依题意得:(12﹣10)x+(23﹣15)(100﹣x)≤40%[10x+15(100﹣x)]
解得,x≥50.
答:至少要购进50只A型文具
17.【详解】解:设有x名八年级学生参加活动,
根据题意,得10(50-x)+20x≥800
解得 x≥30
答:至少有30名八年级学生参加活动.
18.(1)
解:任意实数,,定义关于“”的一种运算如下:,
,
,
∴
∴
(2)
解:,
∴,
∴.
19.【详解】解:>x﹣1,
1+2x>3x﹣3,
2x﹣3x>﹣3﹣1,
﹣x>﹣4,
x<4.
20.【详解】解:(1)当>30时,购买A款垃圾桶个数80-2(-30)=140-2,
∵每个A款垃圾桶进价不低于50元
140-2≥50,
解得≤45
∴当45≥>30时,进价为(140-2)元,
∵某商场向厂家订购了A,B两款垃圾桶工100个,
∴B款垃圾桶个数为(100-)个
根据信息填表如下:
款式 数量(个) 进价(元/个)
A (不超过30个时) 80
(超过30个时)
B 40
故答案为140-2,100-;
(2)①当时,A进价为80元/个,
,
解得,符合题意;
②当45≥>30时,A进价为()元/个,
,
解得,(舍去),
答:商场订购了A款垃圾桶20个或40个.
