第十八章:平行四边形练习题 含解析 2021-2022学年吉林省八年级下学期人教版数学期末试题选编
文档属性
| 名称 | 第十八章:平行四边形练习题 含解析 2021-2022学年吉林省八年级下学期人教版数学期末试题选编 |

|
|
| 格式 | zip | ||
| 文件大小 | 792.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 00:00:00 | ||
图片预览




文档简介
第十八章:平行四边形
一、单选题
1.(2022春·吉林长春·八年级统考期末)如图,已知平行四边形中,,则( )
A.18° B.36° C.72° D.144°
2.(2022春·吉林松原·八年级校考期末)如图, ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
3.(2022春·吉林长春·八年级统考期末)如图,直线,点Q是直线上的动点,点C和点D是直线上的定点,当点Q从左向右运动时,的面积将( ).
A.不变 B.变大 C.变小 D.无法确定
4.(2022春·吉林四平·八年级统考期末)如图,矩形ABCD中,对角线AC和BD交于点O,E为BC中点.若AC=8,∠ACB=30°,则OE的长为( )
A.2 B.3 C.4 D.4
5.(2022春·吉林长春·八年级统考期末)如图,将矩形ABCD沿对角线BD折叠,使点C落在F处,BF交AD于点E.若∠BDC=62°,则∠DEF的度数为( )
A.31° B.28° C.62° D.56°
6.(2022春·吉林长春·八年级统考期末)如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是( )
A.20 B.24 C.40 D.48
7.(2022春·吉林白城·八年级统考期末)□ABCD中,AC、BD是两条对角线,如果添加一个条件,可推出□ABCD是菱形,那么这个条件可以是( )
A.AB=CD B.AC=BD C.AC⊥BD D.AB⊥BD
8.(2022春·吉林四平·八年级统考期末)如图,菱形ABCD的对角线AC、BD相交于点O,BD=6,AC=8,E是CD的中点,则OE的长是( )
A.2.5 B.3 C.4 D.5
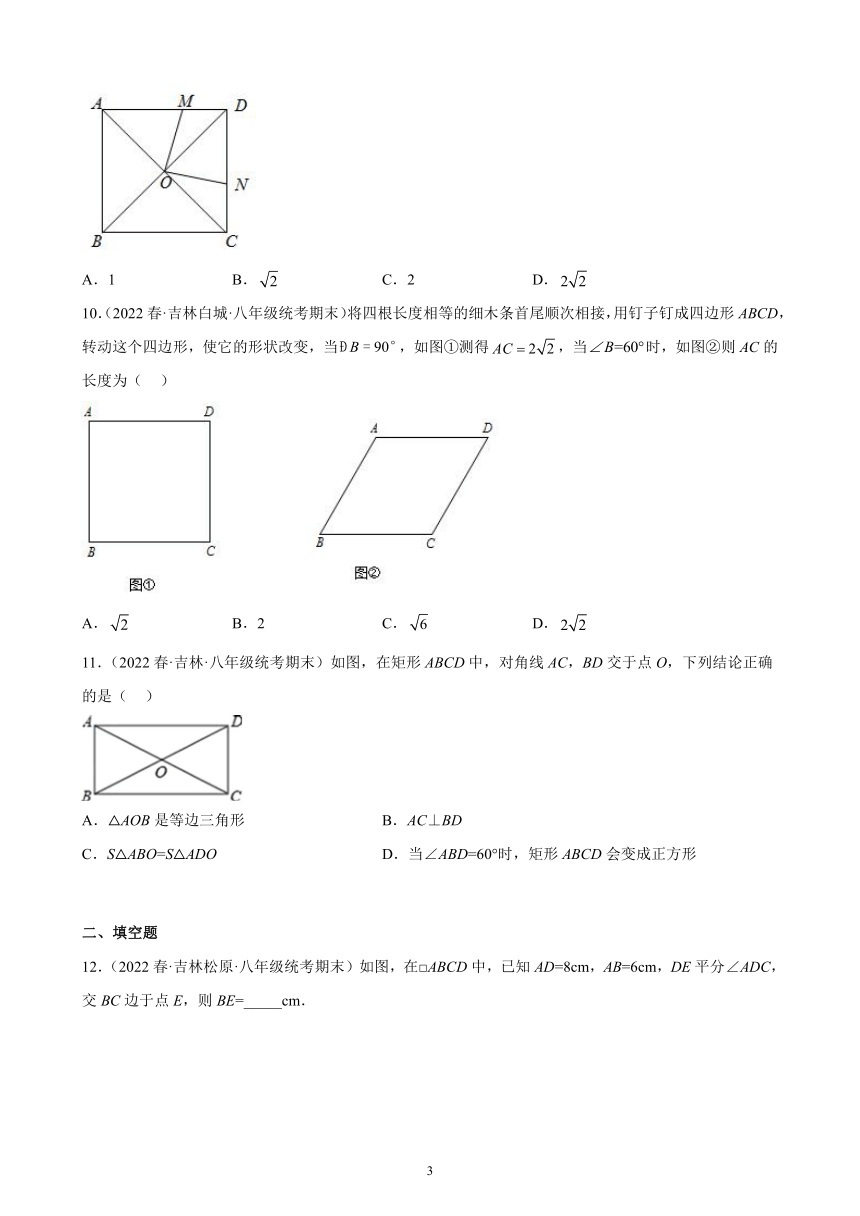
9.(2022春·吉林长春·八年级统考期末)如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.
10.(2022春·吉林白城·八年级统考期末)将四根长度相等的细木条首尾顺次相接,用钉子钉成四边形ABCD,转动这个四边形,使它的形状改变,当,如图①测得,当时,如图②则AC的长度为( )
A. B.2 C. D.
11.(2022春·吉林·八年级统考期末)如图,在矩形ABCD中,对角线AC,BD交于点O,下列结论正确的是( )
A.△AOB是等边三角形 B.AC⊥BD
C.S△ABO=S△ADO D.当∠ABD=60°时,矩形ABCD会变成正方形
二、填空题
12.(2022春·吉林松原·八年级统考期末)如图,在□ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC,交BC边于点E,则BE=_____cm.
13.(2022春·吉林长春·八年级统考期末)如图,E是□ABCD内任意一点,连接AE、BE、CE、DE.若□ABCD的面积是10,则阴影部分图形的面积是 ___.
14.(2022春·吉林四平·八年级统考期末)在□ABCD中,点O是对角线AC、BD的交点,AC⊥BC,且AB=10cm,AD=8cm,则OB=___________cm.
15.(2022春·吉林长春·八年级统考期末)如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件_________(只添一个即可),使四边形ABCD是平行四边形.
16.(2022春·吉林白城·八年级统考期末)如图,是矩形的对角线的中点,是的中点.若,,则四边形的周长为_______.
17.(2022春·吉林松原·八年级校考期末)如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=10,则EF的长为_____.
18.(2022春·吉林四平·八年级统考期末)如图,在平行四边形ABCD中,过AC中点O的直线分别交边BC,AD于点E,F,连接AE,CF.只需添加一个条件即可证明四边形AECF 是菱形,这个条件可以是________(写出一个即可).
19.(2022春·吉林延边·八年级统考期末)如图,在菱形ABCD中,AC、BD交于点O,BC=5,若DE∥AC,CE∥BD,则OE的长为_____.
20.(2022春·吉林白城·八年级统考期末)如图,在边长为的正方形中,点分别是边的中点,连接点分别是的中点,连接,则的长度为__________.
21.(2022春·吉林长春·八年级统考期末)如图,在平面直角坐标系中,正方形ABCD的顶点A在x轴上,顶点D在y轴上,若点B的坐标为(3,1),则点D的坐标为____________.
三、解答题
22.(2022春·吉林白城·八年级统考期末)如图,在 ABCD中,E为BC边上一点,且AB=AE
(1)求证:△ABC≌△EAD;
(2)若∠B=65°,∠EAC=25°,求∠AED的度数.
23.(2022春·吉林长春·八年级统考期末)如图,四边形ABCD为平行四边形,F是CD的中点,连接AF并延长与BC的延长线交于点E.
求证:BC = CE.
24.(2022春·吉林四平·八年级统考期末)如图,在中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.
25.(2022春·吉林松原·八年级校考期末)如图,在中,、分别是边、的中点,延长至点,使得,连结、、.
(1)求证:四边形是平行四边形.
(2)若四边形的面积为,则的面积为______ .
26.(2022春·吉林松原·八年级校考期末)如图,在△ABC中,AB=AC,点D、E分别是线段BC、AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:△BDE≌△FAE;
(2)求证:四边形ADCF为矩形.
27.(2022春·吉林延边·八年级统考期末)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
28.(2022春·吉林白城·八年级统考期末)在矩形ABCD中,连接AC,AC的垂直平分线交AC于点O,分别交AD、BC于点E、F,连接CE和AF.
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形AECF的面积.
29.(2022春·吉林长春·八年级统考期末)如图,菱形的对角线相交于点O,垂直平分,垂足为点E,求的大小.
30.(2022春·吉林白城·八年级统考期末)如图,四边形ABCD是一个正方形花园,E、F是它的两个门,且,要修建两条路BE和AF,这两条路等长吗?它们有什么位置关系?请证明你的猜想.
31.(2022春·吉林长春·八年级统考期末)如图,四边形ABCD是正方形,点P在射线AC上,点E在射线BC上,且PB=PE,连结PD,点O为线段AC中点.
(1)【感知】如图①,当点P在线段AO上时,
①易证:△ABP≌△ADP(不需要证明).进而得到PE与PD的数量关系是 .
②过点P作PM⊥CD于点M,PN⊥BC于点N,易证:Rt△PNE≌Rt△PMD(不需要证明).进而得到PE与PD的位置关系是 .
(2)【探究】如图②,当点P在线段OC上(点P不与点O、C重合)时,试写出PE与PD的数量关系和位置关系,并说明理由.
(3)【应用】如图③,当点P在线段AC的延长线上时,直接写出当AB=3,CP=时线段DE的长.
参考答案:
1.B
【分析】利用平行四边形的对角相等,邻角互补的性质即可解答.
【详解】解:在平行四边形ABCD中,
∵BC∥AD,
∴∠A+∠B=180°,
∵∠B=4∠A,
∴∠A=36°,
∴∠C=∠A=36°,
故选:B.
【点睛】本题考查平行四边形的性质,解题的关键是熟练掌握平行四边形的几何性质.
2.C
【分析】通过平行四边形性质,可计算得;再结合AB⊥AC推导得为直角三角形,通过勾股定理计算得,再结合平行四边形性质,计算得到答案.
【详解】解:∵ ABCD的对角线AC与BD相交于点O,
∴BO=DO,AO=CO,
∵AB⊥AC,AB=4,AC=6,
∴∠BAO=90°,OA=3
∴,
∴BD=2BO=10,
故选:C.
【点睛】此题考查了平行四边形、勾股定理的知识,解题的关键是熟练掌握平行四边形和勾股定理的性质.
3.A
【分析】根据平行线间的距离处处相等,可知的高不变,再结合点C和点D是直线上的定点,易知底边CD的长也是不变的,由三角形面积公式判断的面积不变.
【详解】解:∵,根据平行线间的距离处处相等,
∴点Q到的距离不变,即的高不变,
∵点C和点D是直线上的定点,
∴的底边CD的长也是不变的,
∴的面积不变.
故选:A.
【点睛】本题主要考查了平行线的性质以及三角形面积公式,熟练掌握平行线间的距离处处相等是解题关键.
4.A
【分析】证△AOB是等边三角形,得AB=OA=4,再证OE是△ABC的中位线,即可求解.
【详解】解:∵四边形ABCD是矩形,AC=8,
∴∠ABC=90°,OA=OC=AC=4,OB=OD=BD,AC=BD,
∴OB=OA,
∵∠ACB=30°,
∴∠BAC=60°,
∴△AOB是等边三角形,
∴AB=OA=4,
∵E为BC的中点,
∴BE=CE,
∴OE是△ABC的中位线,
∴OE=AB=2,
故选:A.
【点睛】本题考查了矩形的性质、等边三角形的判定与性质、三角形中位线定理等知识;熟练掌握矩形的性质和三角形中位线定理,证明△AOB为等边三角形是解题的关键.
5.D
【分析】先利用互余计算出∠BDE=28°,再根据平行线的性质得∠CBD=∠BDE=28°,接着根据折叠的性质得∠FBD=∠CBD=28°,然后利用三角形外角性质计算∠DEF的度数,于是得到结论.
【详解】解:∵四边形ABCD为矩形,
∴AD∥BC,∠ADC=90°,
∵,
∵AD∥BC,
∴∠CBD=∠BDE=28°,
∵矩形ABCD沿对角线BD折叠,
∴∠FBD=∠CBD=28°,
∴∠DEF=∠FBD+∠BDE=28°+28°=56°.
故选:D.
【点睛】本题考查了矩形的性质,平行线和折叠的性质,综合运用以上性质是解题的关键.
6.A
【分析】由菱形对角线的性质,相互垂直平分即可得出菱形的边长,菱形四边相等即可得出周长.
【详解】由菱形对角线性质知,AO=AC=3,BO=BD=4,且AO⊥BO,
则AB==5,
故这个菱形的周长L=4AB=20.
故选A.
【点睛】本题考查了菱形面积的计算,考查了勾股定理在直角三角形中的运用,考查了菱形各边长相等的性质,本题中根据勾股定理计算AB的长是解题的关键,难度一般.
7.C
【分析】根据菱形的定义和判定定理逐项作出判断即可.
【详解】解:A. AB=CD,无法判断四边形ABCD是菱形,不合题意;
B. AC=BD,根据对角线相等的平行四边形是矩形可以判断□ABCD是矩形,不合题意;
C. AC⊥BD,根据对角线互相垂直的平行四边形是菱形可以判断□ABCD是菱形,符合题意;
D. AB⊥BD,可以得到∠B=90°,根据有一个角是直角的平行四边形叫矩形可以判断□ABCD是矩形,不合题意.
故选:C
【点睛】本题考查了菱形的判定,熟知菱形的定义和判定定理是解题的关键.
8.A
【分析】根据菱形的性质可得OA=OC==4,OB=OD==3.∠DOC=90°.再根据勾股定理可得CD==5.再由直角三角形斜边上中线的性质可得,OE=CD=2.5.
【详解】解:∵四边形ABCD为菱形,
∴OC=OA==4, OB=OD==3, ∠DOC=90°,
∴CD==5,
∵点E为AB中点,O为AC的中点
∴OE是RtCOD斜边上的中线,
∴OE=CD=2.5.
故选A
【点睛】本题考查了菱形的性质和直角三角形的性质及勾股定理,熟练掌握直角三角形斜边上的中线等于斜边的一半是解题的关键.
9.C
【分析】先证明,再证明四边形MOND的面积等于,的面积,继而解得正方形的面积,据此解题.
【详解】解:在正方形ABCD中,对角线BD⊥AC,
又
四边形MOND的面积是1,
正方形ABCD的面积是4,
故选:C.
【点睛】本题考查正方形的性质、全等三角形的判定与性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.
10.B
【分析】图1中根据勾股定理即可求得正方形的边长,图2根据有一个角是60°的等腰三角形是等边三角形即可求得.
【详解】解:如图1,
∵AB=BC=CD=DA,∠B=90°,
∴四边形ABCD是正方形,
连接AC,则AB2+BC2=AC2,
∴,
如图2,∠B=60°,连接AC,
∵AB=BC,
∴△ABC为等边三角形,
∴,
故选:B.
【点睛】本题考查了正方形的性质,勾股定理以及等边三角形的判定和性质,利用勾股定理得出正方形的边长是关键.
11.C
【分析】依据矩形的对角线的性质可证明OA=OB,故此可对A作出判断,依据矩形的对角线的性质可对B作出判断,证明用含AB、AD的式子表示△ABO和△ADO的面积,从而可判断C,可证明AC与BD不垂直,从而可证明ABCD不是正方形,故此可对D作出判断.
【详解】解:∵ABCD为矩形,
∴AO=AC,BD=BD,AC=BD.
∴OA=OB.
∴△AOB是等腰三角形,但不能推出是等边三角形,
∴选项A错误;
∵矩形的对角线不一定相互垂直,
∴选项B错误;
如图所示:取AB、AD的中点F、E.
∵AF=BF,AO=OC,
∴FO是△ABC的中位线.
∴OFBC,OF=BC.
∵BC⊥AB,FO∥BC,
∴OF⊥AB.
∴
同理:.
∴.
∴选项C正确;
∵∠ABD=60°,OA=OB,
∴△AOB是等边三角形,
∴∠AOB=60°,
∴AC与BD不互相垂直.
∴四边形ABCD不是正方形.
∴选项D错误,
故选:C.
【点睛】本题主要考查的是矩形的性质、三角形中位线的性质、等腰三角形的判断,将△AOB和△AOD的面积转化为矩形面积的是解题的关键.
12.2
【分析】由 ABCD和DE平分∠ADC,可证∠DEC=∠CDE,从而可知△DCE为等腰三角形,则CE=CD,由AD=BC=8cm,AB=CD=6cm即可求出BE.
【详解】解:∵四边形ABCD是平行四边形,
∴∠ADE=∠DEC
∵DE平分∠ADC
∴∠ADE=∠CDE
∴∠DEC=∠CDE
∴CD=CE
∵CD=AB=6cm
∴CE=6cm
∵BC=AD=8cm
∴BE=BC-EC=8-6=2cm.
故答案为2.
【点睛】本题主要考查了平行四边形的性质,在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.
13.5.
【分析】过E作MN⊥BC,交BC于M,交AD于N,△EBC的面积+△EAD的面积=AD EN+BC EM=BC MN=平行四边形ABCD的面积,即可得出阴影部分的面积.
【详解】解:过E作MN⊥BC,交BC于M,交AD于N,如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴EN⊥AD,
∵S△AED=AD EN,S△BCE=BC EM,
∴S△ADE+S△BCE=AD EN+BC EM=BC MN=平行四边形ABCD的面积=×10=5,
∴阴影部分的面积=5,
故答案为:5.
【点睛】此题主要考查了平行四边形的性质、阴影部分面积的计算;熟练掌握平行四边形的性质,关键是掌握平行四边形的面积公式=底×高.
14.cm.
【详解】试题分析:因为AC垂直于BC,AB=10cm,BC=AD=8cm,
所以AC=,所以OC=AC=3cm.
所以OB=cm.
故答案为cm.
考点:1.勾股定理;2.平行四边形的性质.
15.BO=DO
【详解】解:∵AO=CO,BO=DO,∴四边形ABCD是平行四边形.
故答案为:BO=DO.
16.20
【分析】先由,得到,然后结合矩形的性质得到,再结合点和点分别是和的中点得到和的长,最后得到四边形的周长.
【详解】解:,
,
,,
,
点和点分别是和的中点,
,,是的中位线,
,
.
故答案为:20.
【点睛】本题考查了矩形的性质、三角形的中位线定理,解题的关键是熟知矩形的性质.
17.2
【分析】由三角形中位线定理可得DE的长,再由直角三角形斜边上中线的性质可得DF的长,则可得EF的长.
【详解】解:∵DE为△ABC的中位线,
∴DE=BC=5,
∵∠AFB=90°,D是AB 的中点,
∴DF=AB=3,
∴EF=DE﹣DF=2.
故答案为:2.
【点睛】本题考查了三角形中位线定理与直角三角形斜边上中线的性质,掌握这两个知识点是本题的关键所在.
18.(答案不唯一)
【分析】根据菱形的判定即可解.
【详解】是平行四边形
∴AD∥BC
∴∠FAC=∠ECA,∠AFE=∠FEC,
∵AO=CO
∴△AOF≌△COE(AAS)
∴AF=CE
又∵AF=CE
四边形AECF 是平行四边形,
又∵
∴四边形AECF是菱形.
故答案为:(答案不唯一)
【点睛】本题考查了平行四边形的性质、菱形的判定等,熟练掌握菱形判定是解决问题的关键.
19.5
【分析】由菱形的性质可得BC=CD=5,AC⊥BD,由题意可证四边形ODEC是矩形,可得OE=CD=5.
【详解】解:∵四边形ABCD是菱形,
∴BC=CD=5,AC⊥BD,
∵DE∥AC,CE∥BD,
∴四边形ODEC是平行四边形,且AC⊥BD,
∴四边形ODEC是矩形,
∴OE=CD=5,
故答案为5.
【点睛】本题考查了菱形的性质,矩形的判定和性质,证明四边形ODEC是矩形是解题的关键.
20.1
【分析】过E作,过G作,过H作,与相交于I,分别求出HI和GI的长,利用勾股定理即可求解.
【详解】过E作,过G作,过H作,垂足分别为P,R,R,与相交于I,如图,
∵四边形ABCD是正方形,
∴,
,
∴四边形AEPD是矩形,
∴,
∵点E,F分别是AB,BC边的中点,
∴,
,,
∵点G是EC的中点,
是的中位线,
,
同理可求:,
由作图可知四边形HIQP是矩形,
又HP=FC,HI=HR=PC,
而FC=PC,
∴ ,
∴四边形HIQP是正方形,
∴,
∴
是等腰直角三角形,
故答案为:1.
【点睛】此题主要考查了正方形的判定与性质,三角形的中位线与勾股定理等知识,正确作出辅助线是解答此题的关键.
21.(0,2)
【分析】过点B作BE⊥x轴于点E,证明△ODA≌△EAB(AAS),可得OA=BE=1,OD=AE,进而可以解决问题.
【详解】解:如图,过点B作BE⊥x轴于点E,
∵B的坐标为(3,1),
∴OE=3,BE=1,
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠BEA=90°.
∵OA⊥OD,
∴∠AOD=∠BEA=90°.∠DAO+∠ODA=∠BAE+∠DAO=90°,
∴∠ODA=∠BAE,
在△ODA和△EAB中,,
∴△ODA≌△EAB(AAS),
∴OA=BE=1,OD=AE,
∴OD=AE=OE-OA=3-1=2,
∴点D的坐标为(0,2).
故答案为:(0,2).
【点睛】本题考查了坐标与图形性质,正方形的性质,全等三角形的判定和性质,熟练掌握坐标与图形性质,全等三角形的判定和性质等知识点是解题的关键.
22.(1)见解析;(2)∠AED=75°.
【分析】(1)先证明∠B=∠EAD,然后利用SAS可进行全等的证明;
(2)先根据等腰三角形的性质可得∠BAE=50°,求出∠BAC的度数,即可得∠AED的度数.
【详解】(1)证明:∵在平行四边形ABCD中,AD∥BC,BC=AD,
∴∠EAD=∠AEB,
又∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠EAD,
在△ABC和△EAD中,
,
∴△ABC≌△EAD(SAS).
(2)解:∵AB=AE,
∴∠B=∠AEB,
∴∠BAE=50°,
∴∠BAC=∠BAE+∠EAC=50°+25°=75°,
∵△ABC≌△EAD,
∴∠AED=∠BAC=75°.
【点睛】本题考查了平行四边形的性质、全等三角形的判定与性质,注意掌握平行四边形的对边平行且相等的性质.
23.证明见解析
【分析】根据平行四边形的对边平行且相等可得AD=BC,AD∥BC,根据两直线平行,内错角相等可得∠DAF=∠E,∠ADF=∠ECF,根据线段中点的定义可得DF=CF,然后利用“角角边”证明△ADF≌△ECF,根据全等三角形对应边相等可得AD=CE,从而得证.
【详解】∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAF=∠E,∠ADF=∠ECF,
又∵F是CD的中点,即DF=CF,
∴△ADF≌△ECF,
∴AD=CE,
∴BC=CE.
【点睛】1、平行四边形的性质;2、全等三角形的判定与性质
24.见解析
【分析】根据平行四边形的性质可得AF∥EC.AF=EC,然后根据平行四边形的定义即可证得.
【详解】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AF∥EC,
∵BE=FD,
∴BC-BE=AD-FD,
∴AF=EC,
∴四边形AECF是平行四边形.
【点睛】本题考查了平行四边形的性质与判定,熟练掌握平行四边形的性质,证出AF=EC是解决问题的关键.
25.(1)见解析
(2)16
【分析】(1)根据三角形中位线定理可得且.再由,可得,即可求证;
(2)根据,可得四边形与的高相等,设四边形,CF边上的高为,再由,可得,然后根据点D为AB的中点,即可求解.
(1)
证明:、分别是边、的中点,
∴且.
∴,
又,
,
四边形是平行四边形;
(2)
解:∵,
四边形与的高相等,
设四边形中,CF边上的高为,
又,
,
∵点D为AB的中点,
∴.
故答案是:16.
【点睛】本题主要考查了三角形中位线定理,平行四边形的判定和性质,熟练掌握三角形中位线定理,平行四边形的判定和性质是解题的关键.
26.(1)见解析;(2)见解析
【分析】(1)首先根据平行线的性质得到∠AFE=∠DBE,再根据线段中点的定义得到AE=DE,根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到AF=BD,推出四边形ADCF是平行四边形,根据等腰三角形的性质得到∠ADC=90°,于是得到结论.
【详解】(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是线段AD的中点,
∴AE=DE,
∵∠AEF=∠DEB,
∴(AAS);
(2)证明:∵,
∴AF=BD,
∵D是线段BC的中点,
∴BD=CD,
∴AF=CD,
∵AF∥CD,
∴四边形ADCF是平行四边形,
∵AB=AC,
∴,
∴∠ADC=90°,
∴四边形ADCF为矩形.
【点睛】本题主要考查了全等三角形的证明与矩形证明,熟练掌握相关概念是解题关键.
27.(1)见解析(2)成立
【分析】(1)由DF=BE,四边形ABCD为正方形可证△CEB和△CFD全等,从而证出CE=CF.
(2)由(1)得,CE=CF,∠BCE+∠ECD=∠DCF+∠ECD即∠ECF=∠BCD=90°又∠GCE=45°所以可得∠GCE=∠GCF,故可证得△ECG和△FCG全等,即EG=FG=GD+DF.又因为DF=BE,所以可证出GE=BE+GD成立.
【详解】解:(1)在正方形ABCD中,BC=CD,∠B=∠CDF=90°,
∵,
∴△CBE△CDF(SAS).
∴CE=CF.
(2)GE=BE+GD成立.
理由:∵由(1)得:△CBE△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,
又∵∠GCE=45°,
∴∠GCF=∠GCE=45°,CE=CF.
∵∠GCE=∠GCF, GC=GC,
∴△ECG△FCG(SAS).
∴GE=GF.
∴GE=DF+GD=BE+GD.
【点睛】本题考查了以下内容:1.正方形的性质;2.全等三角形的判定与性质;解决本题的关键是理解题意,灵活运用全等三角形的性质与判定.
28.(1)见解析;(2)20
【分析】(1)根据推出:;根据全等得出,推出四边形是平行四边形,再根据即可推出四边形是菱形;
(2)根据线段垂直平分线性质得出,设,推出,,在中,由勾股定理得出方程,求出即可.
【详解】解:(1)证明:是的垂直平分线,
,,
四边形是矩形,
∴AD∥BC,
,
在和中,
,
;
又,
四边形是平行四边形,
又
平行四边形是菱形;
(2)设,
是的垂直平分线,
,,
在中,由勾股定理得:,
,
解得.
,
菱形的周长为20.
【点睛】本题考查了勾股定理,矩形性质,平行四边形的判定,菱形的判定,全等三角形的性质和判定,平行线的性质等知识点的综合运用,用了方程思想.
29.120°
【分析】根据DE垂直平分BC,可得,根据菱形的性质可得,即为等边三角形,则,则问题得解.
【详解】解:在菱形ABCD中,有,且,
∵DE垂直平分BC,
∴,
∴,
∴为等边三角形,
∴,
∵,
∴,
∴,
即∠ABC的度数为120°.
【点睛】本题考查了菱形的性质、等边三角形的判定与性质、平行的性质等知识,证明是等边三角形是解答本题的关键.
30.BE=AF,BE⊥AF,证明见解析
【分析】根据正方形性质可得,AB=AD=CD,又有,因此可以得到,因此可以证明得到,从而证明得到BE=AF,∠AEB=∠DFA,根据三角形内角和定理可以得到∠EAO+∠DFA=90°,等量代换即可得到∠EAO+∠AEB=90°,因此证明得到∠AOE =90°,从而证明得到结论.
【详解】解:猜想BE=AF,BE⊥AF,理由如下:
∵四边形ABCD是正方形
∴AB=AD=CD,∠D=∠BAD=90°
∵,
∴AD-DE=CD-CF,即
在和中,
∴(SAS)
∴BE=AF,∠AEB=∠DFA,
∵∠D=90°
∴∠EAO+∠DFA=90°
∴∠EAO+∠AEB=90°
∴∠AOE=90°
∴BE⊥AF
【点睛】本题考查了正方形的性质,全等三角形的判定和性质,综合运用知识分析推导结论是本题的关键.
31.(1)①;②
(2),
(3)
【分析】(1)①根据正方形的性质可得,即可得出答案;
②由条件可证得四边形是矩形,故,再由角平分线的性质可得出,由,可得,再由得出,即可得出答案;
(2)设交于,正方形的性质可得:,即可得出,,由,即可得出,,再由三角形内角和定理可推导出,可得出,即可得出与的数量关系和位置关系;
(3)设交于,过点作于,由正方形的性质可得:,即可得出,,由,即可得出,,故,再由三角形内角和定理可推导出,可得出,即可得出是等腰直角三角形,由等腰三角形的性质可得出,由,可推导出是等腰直角三角形,故,,由勾股定理即可计算给出,的长度.
【详解】(1)①∵四边形是正方形,
∴,,
又∵,
∴,
∴,
∵,
∴,
故答案为:;
②∵于点,于点,
∴,
∵四边形是正方形,
∴平分,,
∵
∴四边形是矩形,
∴,
∵平分,,,
∴,
在和中,
,
∴,
∴,
∵
∴,
即,
∴,
故答案为:;
(2)与的数量关系和位置关系为:,,理由如下:
设交于,如图②所示:
∵在正方形中,
∴,
∵,
∴
∴,
∵,
∴,,
∵,
∴,
∵,
∴,
∴,
在正方形中:,
∴,
∴;
∴与的数量关系和位置关系为:,
(3)设交于,过点作于,如图③所示
在正方形中:,,,,
∴,
∵,
∴,
∴,,
∵,
∴,,
∵,
∴,
∵,
∴,
∴,
在正方形中: ,
∴,
∴是等腰直角三角形,
∵,,
∴,
∵,
∴是等腰直角三角形,
∴,
∴,
∴,
∴.
【点睛】此题考查了正方形的性质,矩形的判定和性质,勾股定理,全等三角形的判定和性质,综合性较高,掌握以上知识点,准确作出辅助线是解题的关键.
一、单选题
1.(2022春·吉林长春·八年级统考期末)如图,已知平行四边形中,,则( )
A.18° B.36° C.72° D.144°
2.(2022春·吉林松原·八年级校考期末)如图, ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
3.(2022春·吉林长春·八年级统考期末)如图,直线,点Q是直线上的动点,点C和点D是直线上的定点,当点Q从左向右运动时,的面积将( ).
A.不变 B.变大 C.变小 D.无法确定
4.(2022春·吉林四平·八年级统考期末)如图,矩形ABCD中,对角线AC和BD交于点O,E为BC中点.若AC=8,∠ACB=30°,则OE的长为( )
A.2 B.3 C.4 D.4
5.(2022春·吉林长春·八年级统考期末)如图,将矩形ABCD沿对角线BD折叠,使点C落在F处,BF交AD于点E.若∠BDC=62°,则∠DEF的度数为( )
A.31° B.28° C.62° D.56°
6.(2022春·吉林长春·八年级统考期末)如图,菱形ABCD的对角线AC、BD的长分别为6和8,则这个菱形的周长是( )
A.20 B.24 C.40 D.48
7.(2022春·吉林白城·八年级统考期末)□ABCD中,AC、BD是两条对角线,如果添加一个条件,可推出□ABCD是菱形,那么这个条件可以是( )
A.AB=CD B.AC=BD C.AC⊥BD D.AB⊥BD
8.(2022春·吉林四平·八年级统考期末)如图,菱形ABCD的对角线AC、BD相交于点O,BD=6,AC=8,E是CD的中点,则OE的长是( )
A.2.5 B.3 C.4 D.5
9.(2022春·吉林长春·八年级统考期末)如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A.1 B. C.2 D.
10.(2022春·吉林白城·八年级统考期末)将四根长度相等的细木条首尾顺次相接,用钉子钉成四边形ABCD,转动这个四边形,使它的形状改变,当,如图①测得,当时,如图②则AC的长度为( )
A. B.2 C. D.
11.(2022春·吉林·八年级统考期末)如图,在矩形ABCD中,对角线AC,BD交于点O,下列结论正确的是( )
A.△AOB是等边三角形 B.AC⊥BD
C.S△ABO=S△ADO D.当∠ABD=60°时,矩形ABCD会变成正方形
二、填空题
12.(2022春·吉林松原·八年级统考期末)如图,在□ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC,交BC边于点E,则BE=_____cm.
13.(2022春·吉林长春·八年级统考期末)如图,E是□ABCD内任意一点,连接AE、BE、CE、DE.若□ABCD的面积是10,则阴影部分图形的面积是 ___.
14.(2022春·吉林四平·八年级统考期末)在□ABCD中,点O是对角线AC、BD的交点,AC⊥BC,且AB=10cm,AD=8cm,则OB=___________cm.
15.(2022春·吉林长春·八年级统考期末)如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件_________(只添一个即可),使四边形ABCD是平行四边形.
16.(2022春·吉林白城·八年级统考期末)如图,是矩形的对角线的中点,是的中点.若,,则四边形的周长为_______.
17.(2022春·吉林松原·八年级校考期末)如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=10,则EF的长为_____.
18.(2022春·吉林四平·八年级统考期末)如图,在平行四边形ABCD中,过AC中点O的直线分别交边BC,AD于点E,F,连接AE,CF.只需添加一个条件即可证明四边形AECF 是菱形,这个条件可以是________(写出一个即可).
19.(2022春·吉林延边·八年级统考期末)如图,在菱形ABCD中,AC、BD交于点O,BC=5,若DE∥AC,CE∥BD,则OE的长为_____.
20.(2022春·吉林白城·八年级统考期末)如图,在边长为的正方形中,点分别是边的中点,连接点分别是的中点,连接,则的长度为__________.
21.(2022春·吉林长春·八年级统考期末)如图,在平面直角坐标系中,正方形ABCD的顶点A在x轴上,顶点D在y轴上,若点B的坐标为(3,1),则点D的坐标为____________.
三、解答题
22.(2022春·吉林白城·八年级统考期末)如图,在 ABCD中,E为BC边上一点,且AB=AE
(1)求证:△ABC≌△EAD;
(2)若∠B=65°,∠EAC=25°,求∠AED的度数.
23.(2022春·吉林长春·八年级统考期末)如图,四边形ABCD为平行四边形,F是CD的中点,连接AF并延长与BC的延长线交于点E.
求证:BC = CE.
24.(2022春·吉林四平·八年级统考期末)如图,在中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.
25.(2022春·吉林松原·八年级校考期末)如图,在中,、分别是边、的中点,延长至点,使得,连结、、.
(1)求证:四边形是平行四边形.
(2)若四边形的面积为,则的面积为______ .
26.(2022春·吉林松原·八年级校考期末)如图,在△ABC中,AB=AC,点D、E分别是线段BC、AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:△BDE≌△FAE;
(2)求证:四边形ADCF为矩形.
27.(2022春·吉林延边·八年级统考期末)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
28.(2022春·吉林白城·八年级统考期末)在矩形ABCD中,连接AC,AC的垂直平分线交AC于点O,分别交AD、BC于点E、F,连接CE和AF.
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形AECF的面积.
29.(2022春·吉林长春·八年级统考期末)如图,菱形的对角线相交于点O,垂直平分,垂足为点E,求的大小.
30.(2022春·吉林白城·八年级统考期末)如图,四边形ABCD是一个正方形花园,E、F是它的两个门,且,要修建两条路BE和AF,这两条路等长吗?它们有什么位置关系?请证明你的猜想.
31.(2022春·吉林长春·八年级统考期末)如图,四边形ABCD是正方形,点P在射线AC上,点E在射线BC上,且PB=PE,连结PD,点O为线段AC中点.
(1)【感知】如图①,当点P在线段AO上时,
①易证:△ABP≌△ADP(不需要证明).进而得到PE与PD的数量关系是 .
②过点P作PM⊥CD于点M,PN⊥BC于点N,易证:Rt△PNE≌Rt△PMD(不需要证明).进而得到PE与PD的位置关系是 .
(2)【探究】如图②,当点P在线段OC上(点P不与点O、C重合)时,试写出PE与PD的数量关系和位置关系,并说明理由.
(3)【应用】如图③,当点P在线段AC的延长线上时,直接写出当AB=3,CP=时线段DE的长.
参考答案:
1.B
【分析】利用平行四边形的对角相等,邻角互补的性质即可解答.
【详解】解:在平行四边形ABCD中,
∵BC∥AD,
∴∠A+∠B=180°,
∵∠B=4∠A,
∴∠A=36°,
∴∠C=∠A=36°,
故选:B.
【点睛】本题考查平行四边形的性质,解题的关键是熟练掌握平行四边形的几何性质.
2.C
【分析】通过平行四边形性质,可计算得;再结合AB⊥AC推导得为直角三角形,通过勾股定理计算得,再结合平行四边形性质,计算得到答案.
【详解】解:∵ ABCD的对角线AC与BD相交于点O,
∴BO=DO,AO=CO,
∵AB⊥AC,AB=4,AC=6,
∴∠BAO=90°,OA=3
∴,
∴BD=2BO=10,
故选:C.
【点睛】此题考查了平行四边形、勾股定理的知识,解题的关键是熟练掌握平行四边形和勾股定理的性质.
3.A
【分析】根据平行线间的距离处处相等,可知的高不变,再结合点C和点D是直线上的定点,易知底边CD的长也是不变的,由三角形面积公式判断的面积不变.
【详解】解:∵,根据平行线间的距离处处相等,
∴点Q到的距离不变,即的高不变,
∵点C和点D是直线上的定点,
∴的底边CD的长也是不变的,
∴的面积不变.
故选:A.
【点睛】本题主要考查了平行线的性质以及三角形面积公式,熟练掌握平行线间的距离处处相等是解题关键.
4.A
【分析】证△AOB是等边三角形,得AB=OA=4,再证OE是△ABC的中位线,即可求解.
【详解】解:∵四边形ABCD是矩形,AC=8,
∴∠ABC=90°,OA=OC=AC=4,OB=OD=BD,AC=BD,
∴OB=OA,
∵∠ACB=30°,
∴∠BAC=60°,
∴△AOB是等边三角形,
∴AB=OA=4,
∵E为BC的中点,
∴BE=CE,
∴OE是△ABC的中位线,
∴OE=AB=2,
故选:A.
【点睛】本题考查了矩形的性质、等边三角形的判定与性质、三角形中位线定理等知识;熟练掌握矩形的性质和三角形中位线定理,证明△AOB为等边三角形是解题的关键.
5.D
【分析】先利用互余计算出∠BDE=28°,再根据平行线的性质得∠CBD=∠BDE=28°,接着根据折叠的性质得∠FBD=∠CBD=28°,然后利用三角形外角性质计算∠DEF的度数,于是得到结论.
【详解】解:∵四边形ABCD为矩形,
∴AD∥BC,∠ADC=90°,
∵,
∵AD∥BC,
∴∠CBD=∠BDE=28°,
∵矩形ABCD沿对角线BD折叠,
∴∠FBD=∠CBD=28°,
∴∠DEF=∠FBD+∠BDE=28°+28°=56°.
故选:D.
【点睛】本题考查了矩形的性质,平行线和折叠的性质,综合运用以上性质是解题的关键.
6.A
【分析】由菱形对角线的性质,相互垂直平分即可得出菱形的边长,菱形四边相等即可得出周长.
【详解】由菱形对角线性质知,AO=AC=3,BO=BD=4,且AO⊥BO,
则AB==5,
故这个菱形的周长L=4AB=20.
故选A.
【点睛】本题考查了菱形面积的计算,考查了勾股定理在直角三角形中的运用,考查了菱形各边长相等的性质,本题中根据勾股定理计算AB的长是解题的关键,难度一般.
7.C
【分析】根据菱形的定义和判定定理逐项作出判断即可.
【详解】解:A. AB=CD,无法判断四边形ABCD是菱形,不合题意;
B. AC=BD,根据对角线相等的平行四边形是矩形可以判断□ABCD是矩形,不合题意;
C. AC⊥BD,根据对角线互相垂直的平行四边形是菱形可以判断□ABCD是菱形,符合题意;
D. AB⊥BD,可以得到∠B=90°,根据有一个角是直角的平行四边形叫矩形可以判断□ABCD是矩形,不合题意.
故选:C
【点睛】本题考查了菱形的判定,熟知菱形的定义和判定定理是解题的关键.
8.A
【分析】根据菱形的性质可得OA=OC==4,OB=OD==3.∠DOC=90°.再根据勾股定理可得CD==5.再由直角三角形斜边上中线的性质可得,OE=CD=2.5.
【详解】解:∵四边形ABCD为菱形,
∴OC=OA==4, OB=OD==3, ∠DOC=90°,
∴CD==5,
∵点E为AB中点,O为AC的中点
∴OE是RtCOD斜边上的中线,
∴OE=CD=2.5.
故选A
【点睛】本题考查了菱形的性质和直角三角形的性质及勾股定理,熟练掌握直角三角形斜边上的中线等于斜边的一半是解题的关键.
9.C
【分析】先证明,再证明四边形MOND的面积等于,的面积,继而解得正方形的面积,据此解题.
【详解】解:在正方形ABCD中,对角线BD⊥AC,
又
四边形MOND的面积是1,
正方形ABCD的面积是4,
故选:C.
【点睛】本题考查正方形的性质、全等三角形的判定与性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.
10.B
【分析】图1中根据勾股定理即可求得正方形的边长,图2根据有一个角是60°的等腰三角形是等边三角形即可求得.
【详解】解:如图1,
∵AB=BC=CD=DA,∠B=90°,
∴四边形ABCD是正方形,
连接AC,则AB2+BC2=AC2,
∴,
如图2,∠B=60°,连接AC,
∵AB=BC,
∴△ABC为等边三角形,
∴,
故选:B.
【点睛】本题考查了正方形的性质,勾股定理以及等边三角形的判定和性质,利用勾股定理得出正方形的边长是关键.
11.C
【分析】依据矩形的对角线的性质可证明OA=OB,故此可对A作出判断,依据矩形的对角线的性质可对B作出判断,证明用含AB、AD的式子表示△ABO和△ADO的面积,从而可判断C,可证明AC与BD不垂直,从而可证明ABCD不是正方形,故此可对D作出判断.
【详解】解:∵ABCD为矩形,
∴AO=AC,BD=BD,AC=BD.
∴OA=OB.
∴△AOB是等腰三角形,但不能推出是等边三角形,
∴选项A错误;
∵矩形的对角线不一定相互垂直,
∴选项B错误;
如图所示:取AB、AD的中点F、E.
∵AF=BF,AO=OC,
∴FO是△ABC的中位线.
∴OFBC,OF=BC.
∵BC⊥AB,FO∥BC,
∴OF⊥AB.
∴
同理:.
∴.
∴选项C正确;
∵∠ABD=60°,OA=OB,
∴△AOB是等边三角形,
∴∠AOB=60°,
∴AC与BD不互相垂直.
∴四边形ABCD不是正方形.
∴选项D错误,
故选:C.
【点睛】本题主要考查的是矩形的性质、三角形中位线的性质、等腰三角形的判断,将△AOB和△AOD的面积转化为矩形面积的是解题的关键.
12.2
【分析】由 ABCD和DE平分∠ADC,可证∠DEC=∠CDE,从而可知△DCE为等腰三角形,则CE=CD,由AD=BC=8cm,AB=CD=6cm即可求出BE.
【详解】解:∵四边形ABCD是平行四边形,
∴∠ADE=∠DEC
∵DE平分∠ADC
∴∠ADE=∠CDE
∴∠DEC=∠CDE
∴CD=CE
∵CD=AB=6cm
∴CE=6cm
∵BC=AD=8cm
∴BE=BC-EC=8-6=2cm.
故答案为2.
【点睛】本题主要考查了平行四边形的性质,在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.
13.5.
【分析】过E作MN⊥BC,交BC于M,交AD于N,△EBC的面积+△EAD的面积=AD EN+BC EM=BC MN=平行四边形ABCD的面积,即可得出阴影部分的面积.
【详解】解:过E作MN⊥BC,交BC于M,交AD于N,如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴EN⊥AD,
∵S△AED=AD EN,S△BCE=BC EM,
∴S△ADE+S△BCE=AD EN+BC EM=BC MN=平行四边形ABCD的面积=×10=5,
∴阴影部分的面积=5,
故答案为:5.
【点睛】此题主要考查了平行四边形的性质、阴影部分面积的计算;熟练掌握平行四边形的性质,关键是掌握平行四边形的面积公式=底×高.
14.cm.
【详解】试题分析:因为AC垂直于BC,AB=10cm,BC=AD=8cm,
所以AC=,所以OC=AC=3cm.
所以OB=cm.
故答案为cm.
考点:1.勾股定理;2.平行四边形的性质.
15.BO=DO
【详解】解:∵AO=CO,BO=DO,∴四边形ABCD是平行四边形.
故答案为:BO=DO.
16.20
【分析】先由,得到,然后结合矩形的性质得到,再结合点和点分别是和的中点得到和的长,最后得到四边形的周长.
【详解】解:,
,
,,
,
点和点分别是和的中点,
,,是的中位线,
,
.
故答案为:20.
【点睛】本题考查了矩形的性质、三角形的中位线定理,解题的关键是熟知矩形的性质.
17.2
【分析】由三角形中位线定理可得DE的长,再由直角三角形斜边上中线的性质可得DF的长,则可得EF的长.
【详解】解:∵DE为△ABC的中位线,
∴DE=BC=5,
∵∠AFB=90°,D是AB 的中点,
∴DF=AB=3,
∴EF=DE﹣DF=2.
故答案为:2.
【点睛】本题考查了三角形中位线定理与直角三角形斜边上中线的性质,掌握这两个知识点是本题的关键所在.
18.(答案不唯一)
【分析】根据菱形的判定即可解.
【详解】是平行四边形
∴AD∥BC
∴∠FAC=∠ECA,∠AFE=∠FEC,
∵AO=CO
∴△AOF≌△COE(AAS)
∴AF=CE
又∵AF=CE
四边形AECF 是平行四边形,
又∵
∴四边形AECF是菱形.
故答案为:(答案不唯一)
【点睛】本题考查了平行四边形的性质、菱形的判定等,熟练掌握菱形判定是解决问题的关键.
19.5
【分析】由菱形的性质可得BC=CD=5,AC⊥BD,由题意可证四边形ODEC是矩形,可得OE=CD=5.
【详解】解:∵四边形ABCD是菱形,
∴BC=CD=5,AC⊥BD,
∵DE∥AC,CE∥BD,
∴四边形ODEC是平行四边形,且AC⊥BD,
∴四边形ODEC是矩形,
∴OE=CD=5,
故答案为5.
【点睛】本题考查了菱形的性质,矩形的判定和性质,证明四边形ODEC是矩形是解题的关键.
20.1
【分析】过E作,过G作,过H作,与相交于I,分别求出HI和GI的长,利用勾股定理即可求解.
【详解】过E作,过G作,过H作,垂足分别为P,R,R,与相交于I,如图,
∵四边形ABCD是正方形,
∴,
,
∴四边形AEPD是矩形,
∴,
∵点E,F分别是AB,BC边的中点,
∴,
,,
∵点G是EC的中点,
是的中位线,
,
同理可求:,
由作图可知四边形HIQP是矩形,
又HP=FC,HI=HR=PC,
而FC=PC,
∴ ,
∴四边形HIQP是正方形,
∴,
∴
是等腰直角三角形,
故答案为:1.
【点睛】此题主要考查了正方形的判定与性质,三角形的中位线与勾股定理等知识,正确作出辅助线是解答此题的关键.
21.(0,2)
【分析】过点B作BE⊥x轴于点E,证明△ODA≌△EAB(AAS),可得OA=BE=1,OD=AE,进而可以解决问题.
【详解】解:如图,过点B作BE⊥x轴于点E,
∵B的坐标为(3,1),
∴OE=3,BE=1,
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠BEA=90°.
∵OA⊥OD,
∴∠AOD=∠BEA=90°.∠DAO+∠ODA=∠BAE+∠DAO=90°,
∴∠ODA=∠BAE,
在△ODA和△EAB中,,
∴△ODA≌△EAB(AAS),
∴OA=BE=1,OD=AE,
∴OD=AE=OE-OA=3-1=2,
∴点D的坐标为(0,2).
故答案为:(0,2).
【点睛】本题考查了坐标与图形性质,正方形的性质,全等三角形的判定和性质,熟练掌握坐标与图形性质,全等三角形的判定和性质等知识点是解题的关键.
22.(1)见解析;(2)∠AED=75°.
【分析】(1)先证明∠B=∠EAD,然后利用SAS可进行全等的证明;
(2)先根据等腰三角形的性质可得∠BAE=50°,求出∠BAC的度数,即可得∠AED的度数.
【详解】(1)证明:∵在平行四边形ABCD中,AD∥BC,BC=AD,
∴∠EAD=∠AEB,
又∵AB=AE,
∴∠B=∠AEB,
∴∠B=∠EAD,
在△ABC和△EAD中,
,
∴△ABC≌△EAD(SAS).
(2)解:∵AB=AE,
∴∠B=∠AEB,
∴∠BAE=50°,
∴∠BAC=∠BAE+∠EAC=50°+25°=75°,
∵△ABC≌△EAD,
∴∠AED=∠BAC=75°.
【点睛】本题考查了平行四边形的性质、全等三角形的判定与性质,注意掌握平行四边形的对边平行且相等的性质.
23.证明见解析
【分析】根据平行四边形的对边平行且相等可得AD=BC,AD∥BC,根据两直线平行,内错角相等可得∠DAF=∠E,∠ADF=∠ECF,根据线段中点的定义可得DF=CF,然后利用“角角边”证明△ADF≌△ECF,根据全等三角形对应边相等可得AD=CE,从而得证.
【详解】∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠DAF=∠E,∠ADF=∠ECF,
又∵F是CD的中点,即DF=CF,
∴△ADF≌△ECF,
∴AD=CE,
∴BC=CE.
【点睛】1、平行四边形的性质;2、全等三角形的判定与性质
24.见解析
【分析】根据平行四边形的性质可得AF∥EC.AF=EC,然后根据平行四边形的定义即可证得.
【详解】证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴AF∥EC,
∵BE=FD,
∴BC-BE=AD-FD,
∴AF=EC,
∴四边形AECF是平行四边形.
【点睛】本题考查了平行四边形的性质与判定,熟练掌握平行四边形的性质,证出AF=EC是解决问题的关键.
25.(1)见解析
(2)16
【分析】(1)根据三角形中位线定理可得且.再由,可得,即可求证;
(2)根据,可得四边形与的高相等,设四边形,CF边上的高为,再由,可得,然后根据点D为AB的中点,即可求解.
(1)
证明:、分别是边、的中点,
∴且.
∴,
又,
,
四边形是平行四边形;
(2)
解:∵,
四边形与的高相等,
设四边形中,CF边上的高为,
又,
,
∵点D为AB的中点,
∴.
故答案是:16.
【点睛】本题主要考查了三角形中位线定理,平行四边形的判定和性质,熟练掌握三角形中位线定理,平行四边形的判定和性质是解题的关键.
26.(1)见解析;(2)见解析
【分析】(1)首先根据平行线的性质得到∠AFE=∠DBE,再根据线段中点的定义得到AE=DE,根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到AF=BD,推出四边形ADCF是平行四边形,根据等腰三角形的性质得到∠ADC=90°,于是得到结论.
【详解】(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是线段AD的中点,
∴AE=DE,
∵∠AEF=∠DEB,
∴(AAS);
(2)证明:∵,
∴AF=BD,
∵D是线段BC的中点,
∴BD=CD,
∴AF=CD,
∵AF∥CD,
∴四边形ADCF是平行四边形,
∵AB=AC,
∴,
∴∠ADC=90°,
∴四边形ADCF为矩形.
【点睛】本题主要考查了全等三角形的证明与矩形证明,熟练掌握相关概念是解题关键.
27.(1)见解析(2)成立
【分析】(1)由DF=BE,四边形ABCD为正方形可证△CEB和△CFD全等,从而证出CE=CF.
(2)由(1)得,CE=CF,∠BCE+∠ECD=∠DCF+∠ECD即∠ECF=∠BCD=90°又∠GCE=45°所以可得∠GCE=∠GCF,故可证得△ECG和△FCG全等,即EG=FG=GD+DF.又因为DF=BE,所以可证出GE=BE+GD成立.
【详解】解:(1)在正方形ABCD中,BC=CD,∠B=∠CDF=90°,
∵,
∴△CBE△CDF(SAS).
∴CE=CF.
(2)GE=BE+GD成立.
理由:∵由(1)得:△CBE△CDF,
∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,
又∵∠GCE=45°,
∴∠GCF=∠GCE=45°,CE=CF.
∵∠GCE=∠GCF, GC=GC,
∴△ECG△FCG(SAS).
∴GE=GF.
∴GE=DF+GD=BE+GD.
【点睛】本题考查了以下内容:1.正方形的性质;2.全等三角形的判定与性质;解决本题的关键是理解题意,灵活运用全等三角形的性质与判定.
28.(1)见解析;(2)20
【分析】(1)根据推出:;根据全等得出,推出四边形是平行四边形,再根据即可推出四边形是菱形;
(2)根据线段垂直平分线性质得出,设,推出,,在中,由勾股定理得出方程,求出即可.
【详解】解:(1)证明:是的垂直平分线,
,,
四边形是矩形,
∴AD∥BC,
,
在和中,
,
;
又,
四边形是平行四边形,
又
平行四边形是菱形;
(2)设,
是的垂直平分线,
,,
在中,由勾股定理得:,
,
解得.
,
菱形的周长为20.
【点睛】本题考查了勾股定理,矩形性质,平行四边形的判定,菱形的判定,全等三角形的性质和判定,平行线的性质等知识点的综合运用,用了方程思想.
29.120°
【分析】根据DE垂直平分BC,可得,根据菱形的性质可得,即为等边三角形,则,则问题得解.
【详解】解:在菱形ABCD中,有,且,
∵DE垂直平分BC,
∴,
∴,
∴为等边三角形,
∴,
∵,
∴,
∴,
即∠ABC的度数为120°.
【点睛】本题考查了菱形的性质、等边三角形的判定与性质、平行的性质等知识,证明是等边三角形是解答本题的关键.
30.BE=AF,BE⊥AF,证明见解析
【分析】根据正方形性质可得,AB=AD=CD,又有,因此可以得到,因此可以证明得到,从而证明得到BE=AF,∠AEB=∠DFA,根据三角形内角和定理可以得到∠EAO+∠DFA=90°,等量代换即可得到∠EAO+∠AEB=90°,因此证明得到∠AOE =90°,从而证明得到结论.
【详解】解:猜想BE=AF,BE⊥AF,理由如下:
∵四边形ABCD是正方形
∴AB=AD=CD,∠D=∠BAD=90°
∵,
∴AD-DE=CD-CF,即
在和中,
∴(SAS)
∴BE=AF,∠AEB=∠DFA,
∵∠D=90°
∴∠EAO+∠DFA=90°
∴∠EAO+∠AEB=90°
∴∠AOE=90°
∴BE⊥AF
【点睛】本题考查了正方形的性质,全等三角形的判定和性质,综合运用知识分析推导结论是本题的关键.
31.(1)①;②
(2),
(3)
【分析】(1)①根据正方形的性质可得,即可得出答案;
②由条件可证得四边形是矩形,故,再由角平分线的性质可得出,由,可得,再由得出,即可得出答案;
(2)设交于,正方形的性质可得:,即可得出,,由,即可得出,,再由三角形内角和定理可推导出,可得出,即可得出与的数量关系和位置关系;
(3)设交于,过点作于,由正方形的性质可得:,即可得出,,由,即可得出,,故,再由三角形内角和定理可推导出,可得出,即可得出是等腰直角三角形,由等腰三角形的性质可得出,由,可推导出是等腰直角三角形,故,,由勾股定理即可计算给出,的长度.
【详解】(1)①∵四边形是正方形,
∴,,
又∵,
∴,
∴,
∵,
∴,
故答案为:;
②∵于点,于点,
∴,
∵四边形是正方形,
∴平分,,
∵
∴四边形是矩形,
∴,
∵平分,,,
∴,
在和中,
,
∴,
∴,
∵
∴,
即,
∴,
故答案为:;
(2)与的数量关系和位置关系为:,,理由如下:
设交于,如图②所示:
∵在正方形中,
∴,
∵,
∴
∴,
∵,
∴,,
∵,
∴,
∵,
∴,
∴,
在正方形中:,
∴,
∴;
∴与的数量关系和位置关系为:,
(3)设交于,过点作于,如图③所示
在正方形中:,,,,
∴,
∵,
∴,
∴,,
∵,
∴,,
∵,
∴,
∵,
∴,
∴,
在正方形中: ,
∴,
∴是等腰直角三角形,
∵,,
∴,
∵,
∴是等腰直角三角形,
∴,
∴,
∴,
∴.
【点睛】此题考查了正方形的性质,矩形的判定和性质,勾股定理,全等三角形的判定和性质,综合性较高,掌握以上知识点,准确作出辅助线是解题的关键.
