二次函数的图象和性质(4)[下学期]

课件21张PPT。二次函数y=a(x+h)2+k的
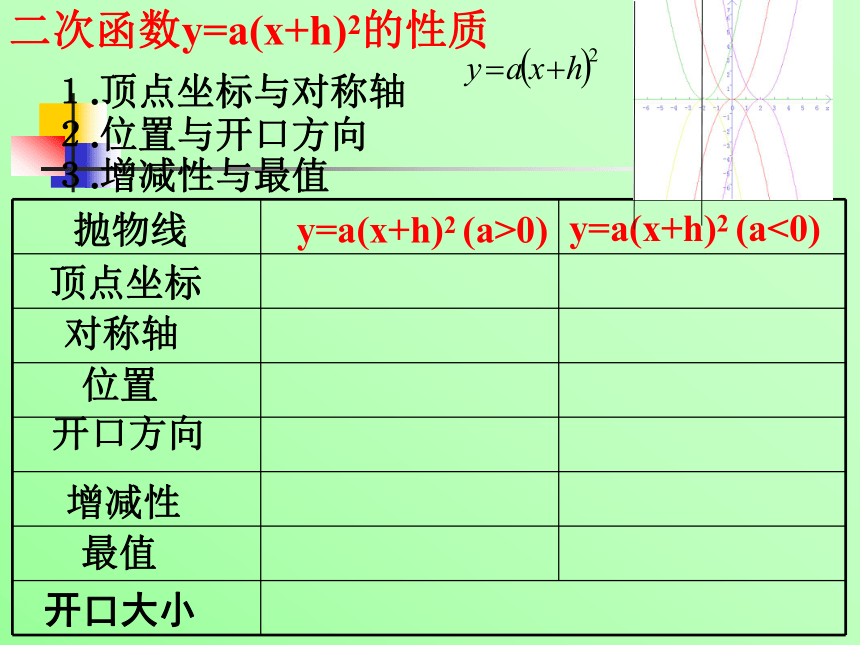
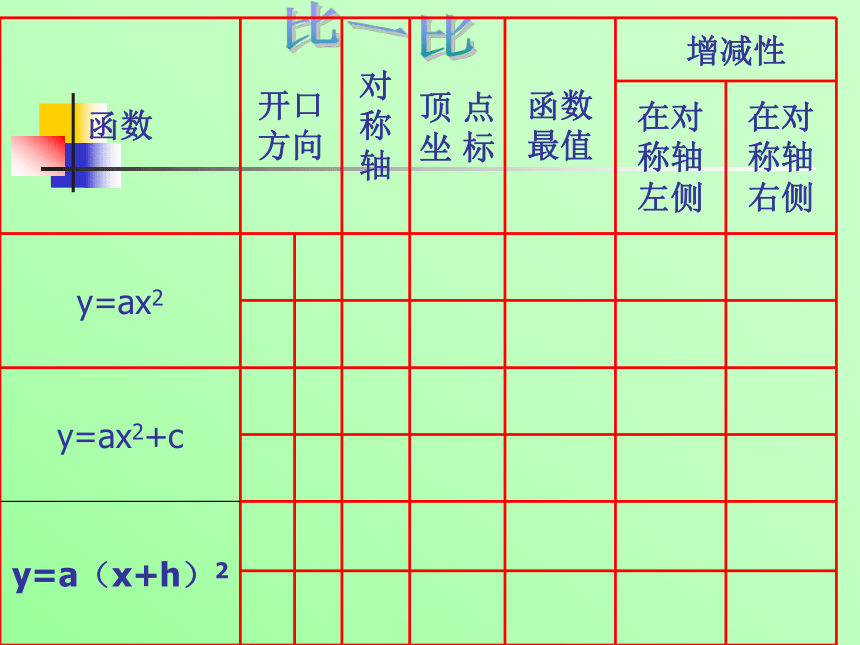
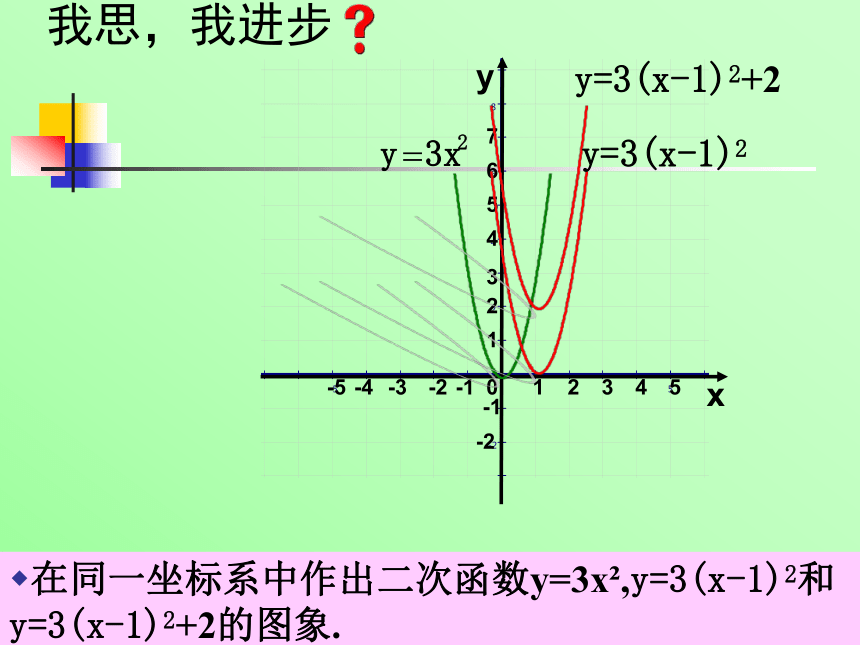
图象和性质xy二次函数y=a(x+h)2的性质１.顶点坐标与对称轴２.位置与开口方向３.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=a(x+h)2 (a>0)y=a(x+h)2 (a<0)比一比回顾练习:填空题
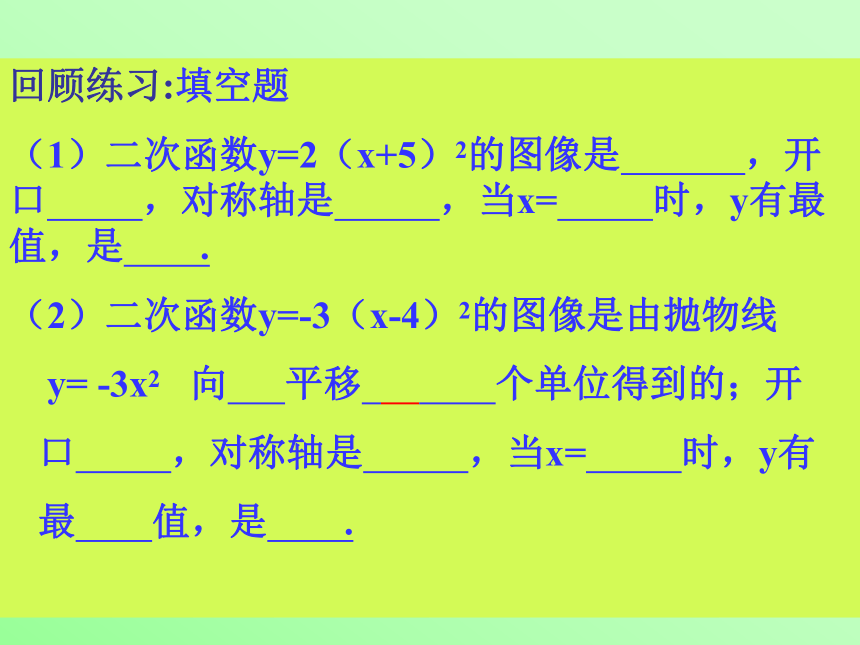
（1）二次函数y=2（x+5）2的图像是 ，开 口 ，对称轴是 ，当x= 时，y有最 值，是 .
（2）二次函数y=-3（x-4）2的图像是由抛物线
y= -3x2 向 平移 个单位得到的；开
口 ，对称轴是 ，当x= 时，y有
最 值，是 .
（3）将二次函数y=2x2的图像向右平移3个单位后得到函数 的图像，其对称轴是 ，顶点是 ，当x 时，y随x的增大而增大；当x 时，y随x的增大而减小.
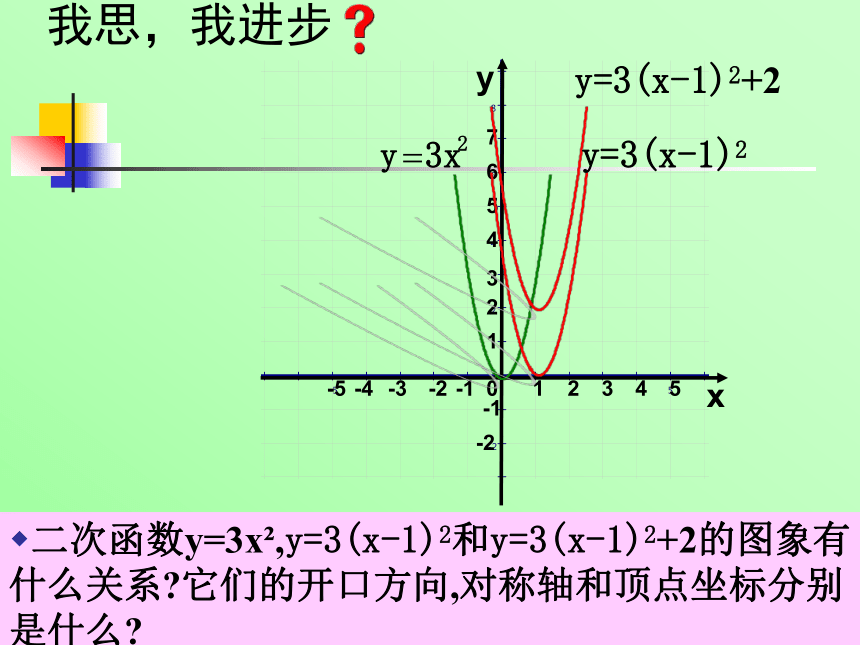
（4）将二次函数y= -3（x-2）2的图像向左平移3个单位后得到函数 的图像，其顶点坐标是 ，对称轴是 ，当x= 时，y有最 值，是 .试一试（5）将函数y=3（x－4）2的图象沿x轴对折后得到的函数解析式是 ； 将函数y=3（x－4）2的图象沿y轴对折后得到的函数解析式是 ；（6）把抛物线y=a（x-4）2向左平移6个单位后得到抛物线y=- 3（x-h）2的图象，则 a= ，h= .若抛物线y= a（x-4）2的顶点A，且与y轴交于点B，抛物线y= - 3（x-h）2的顶点是M，则SΔMAB= .试一试（7）将抛物线y=2x2－3先向上平移3单位，就得到函数 的图象，在向 平移 个单位得到函数y= 2（x-3）2的图象.（8）函数y=（3x+6）2的图象是由函数 的图象向左平移5个单位得到的，其图象开口向 ，对称轴是 ，顶点坐标是 ，当x 时，y随x的增大而增大，当x= 时，y有最 值是 . 我思，我进步在同一坐标系中作出二次函数y=3x2,y=3(x-1)2和y=3(x-1)2+2的图象.y=3(x-1)2y=3(x-1)2+2我思，我进步y=3(x-1)2y=3(x-1)2+2二次函数y=3x2,y=3(x-1)2和y=3(x-1)2+2的图象有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么? 我思，我进步y=3(x-1)2y=3(x-1)2+2二次函数y=3(x-1)2+2的图象和抛物线y=3x2,y=3(x-1)2有什么关系?它的开口方向,对称轴和顶点坐标分别是什么?我思，我进步y=3(x-1)2y=3(x-1)2+2想一想,二次函数y=-3(x-1)2+2和y=-3x2,y=-3(x-1)2的图象有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么?再作图看一看．yX=1我思，我进步二次函数y=-3(x-1)2+2
与y=-3(x-1)2-2和y=-3x2
y=-3(x-1)2的图象有什么关系?它们是轴对称图形 吗?它的开口方向、对称轴和顶点坐标分别是什么? 当x取哪些值时，y的值随x值的增大而增大? 当x取哪些值时，y的值随x值的增大而减小?
二次函数y=a(x+h)2+k与y=ax2的关系 一般地,由y=ax2的图象便可得到二次函数y=a(x+h)2+k的图象:y=a(x+h)2+k(a≠0) 的图象可以看成y=ax2的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向左平移;当h<0时,向右平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.
因此,二次函数y=a(x+h)2+k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标与a,h,k的值有关. 1、平移关系当h>0时,向左平移当h<0时,向右平移y=ax2y=a(x+h)2当k>0时,向上平移当k<0时,向下平移y=a(x+h)2+k二次函数y=a(x+h)2+k与y=ax2的关系y=ax2+k二次函数y=a(x+h)2+k的图象和性质１.顶点坐标与对称轴２.位置与开口方向３.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=a(x+h)2+k(a>0)y=a(x+h)2+k(a<0)（-h，k）（-h，k）直线x=-h直线x=-h由h和k的符号确定由h和k的符号确定向上向下当x=-h时,最小值为k.当x=-h时,最大值为k.在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表：悟出真谛,练出本事1.指出下列函数图象的开口方向对称轴和顶点坐标:2.(1)二次函数y=3(x+1)2的图象与二次函数y=3x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
(2)二次函数y=-3(x-2)2+4的图象与二次函数 y=-3x2的图象有什么关系?
(3)对于二次函数y=3(x+1)2,当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小?二次函数y=3(x+1)2+4呢? 驶向胜利的彼岸 1.指出下列函数图象的开口方向,对称轴和顶点坐标.必要时作出草图进行验证.2.填写下表: 你认为今天这节课最需要掌握的是 ________________ ？ 1.相同点: (1)形状相同(图像的形状都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 . 二次函数y=a(x+h)2+k与=ax2的关系2.不同点: 只是位置不同
(1)顶点不同:分别是(-h,k)和(0,0).
(2)对称轴不同:分别是直线x= -h和y轴.
(3)最值不同:分别是k和0.
3.联系: y=a(x+h)2+k(a≠0) 的图象可以看成y=ax2的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向左平移;当h<0时,向右平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.二次函数y=a(x+h)2+k与=ax2的关系结束寄语读书要从薄到厚,再从厚到薄.再见