二次函数的图象和性质(5)[下学期]
图片预览




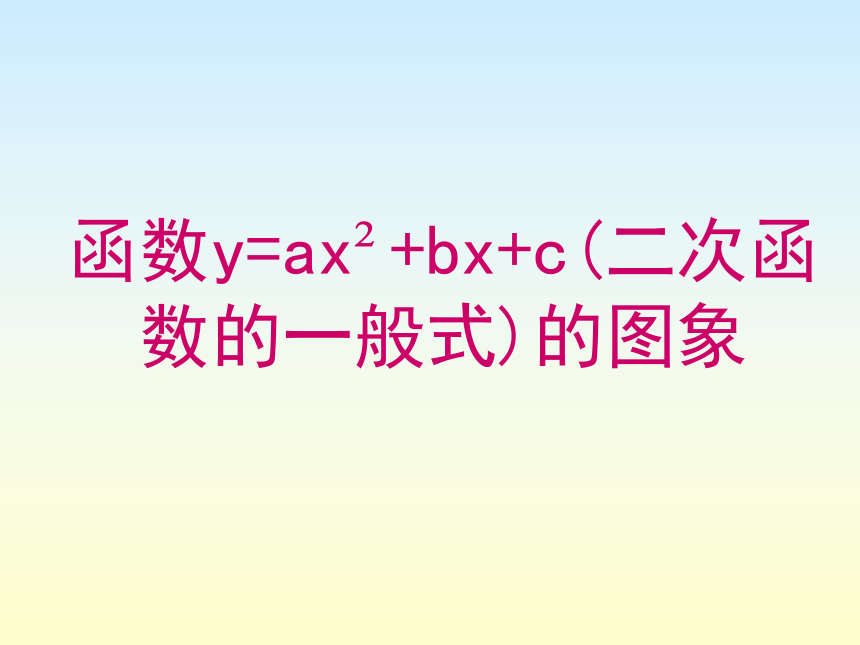


文档简介
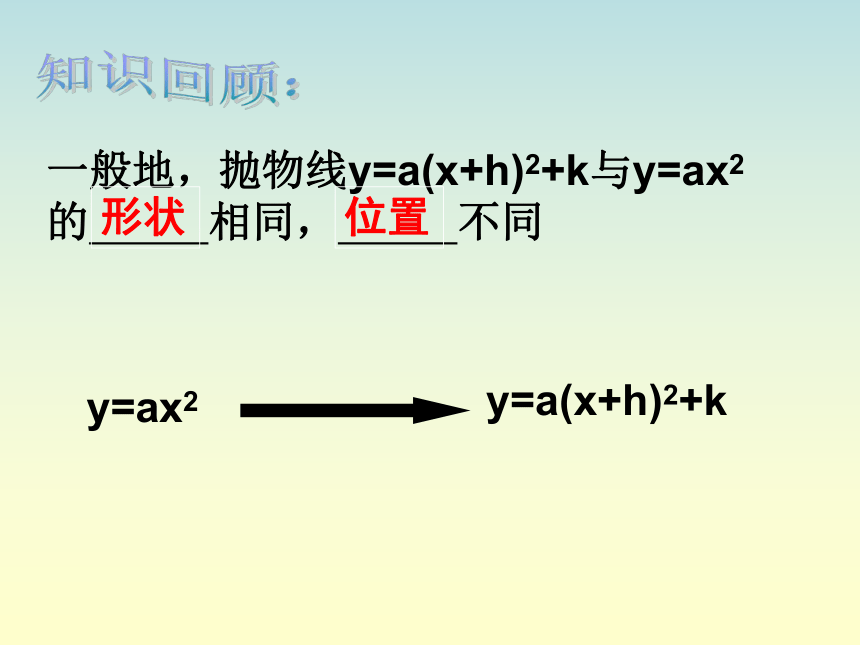
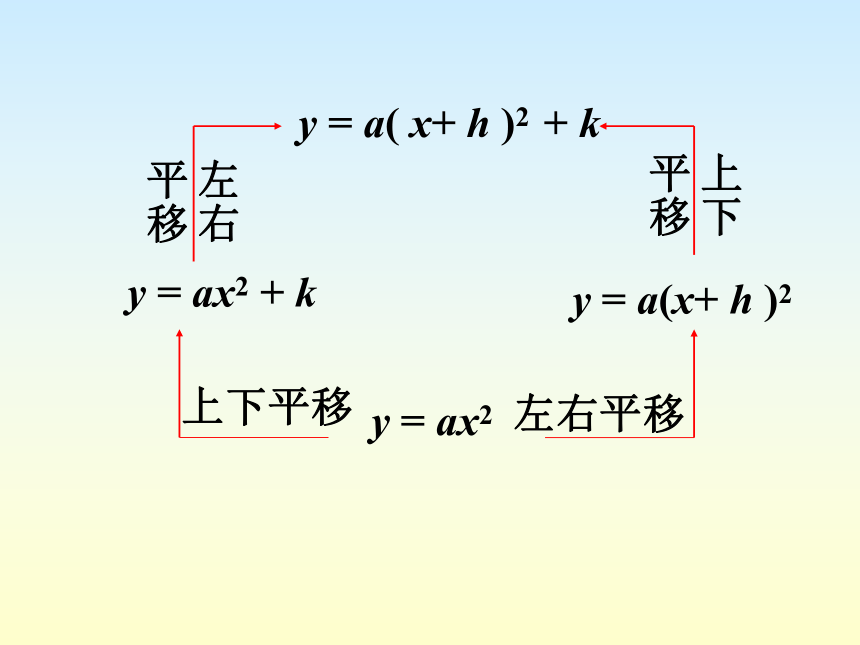
课件20张PPT。二次函数的图象和性质一般地,抛物线y=a(x+h)2+k与y=ax2的 相同, 不同知识回顾:y=ax2y=a(x+h)2+k形状位置y = ax2y = ax2 + k y = a(x+ h )2y = a( x+ h )2 + k上下平移左右平移上下平移左右平移抛物线y=a(x+h)2+k的图像与性质:1.当a﹥0时,开口 ,
当a﹤0时,开口 ,
2.对称轴是 ;
3.顶点坐标是 。向上向下(-h,k)直线X=-h向上( 1 , -2 )向下向下( 3 , 7)( 2 , -6 )向上直线x=-3直线x=1直线x=3直线x=2( -3, 5 )练习:注意函数y=2(x+3)2+5其实就是函数y=2x2+12x +23函数y = -3(x-1)2 -2其实就是函数y=-3x2+6x -5…..倒过来函数y=2x2+12x +23其实就是函数y=2(x+3)2+5函数y=-3x2+6x -5其实就是函数y = -3(x-1)2 -2二次函数y=3x2-6x+5的图象是什么形状?它与我们已经作过的二次函数的图象有什么关系?你用什么方法来研究它? 函数y=ax2+bx+c(二次函数的一般式)的图象 你能用配方的方法把y=3x2-6x+5变形成
y=a(x+m)2+k的形式吗?y=3x2-6x+5=3(x-1)2+2它的顶点坐标是 ,
对称轴是 . 总结:一般地,求形如y=ax2+bx+c的顶点及对称轴,我们可以用配方的方法。 y=-2x2-4x+3的顶点坐标是____ y=2x2+bx+c的顶点坐标是(1,-2),求b,c想一想: 你能说出函数y=ax2+bx+c(a≠0)的对称轴和它的顶点坐标最值吗?
函数y=ax2+bx+c经过配方变形后,可化为:y你能说出它的最值情况吗?1、写出下列抛物线的开口方向、对称轴及顶点坐标,当x为何值时y的值最大(小)? ?(1)y=3x2+2x(2)y=-x2-2x(3)y=-2x2+8x-8练习:3、若一次函数y=-2x+c与二次函数y=ax2 +bx-4
的图象都经过点A(1,-1),二次函数的对称轴直线
是x=-1,请求出一次函数和二次函数的表达式. 2、当m=___时,抛物线y=mx2 +2(m+2)x+m+3的
对称轴是y轴;
当m=_____时,图象与y轴交点的纵坐标是1;
当m=_____时,函数的最小值是-2. 4.写出一个二次函数的解析式,使它的顶点在第二象限且开口向下(要求用一般式表示)求y=x2+2x-8与坐标轴的交点。根据图象回答
何时y<0?
何时y>0?考点训练1、已知二次函数y=ax2+bx+c的图象如图所示
(1)求解析式
(2)何时 y=3?
(3)根据图象回答:
当x 时,y>0。2.如图,在同一坐标系中,函数y=ax+b与y=ax2+bx(ab≠0)的图象只可能是( ) 3.用总长为60m的篱笆墙围成矩形场地,矩形面积S随矩形一边长L的变化而变化,当L多少时,场地的面积S最大? 1.心理学家发现,学生对概念的接受能力y与提出:
概念所用的时间x(分钟)之间满足函数关系:
y=-0.1x2 +2.6x+43(0≤x≤30),y值越大表示接受能力越强.
(1)x在什么范围内,学生的接受能力逐步增加?x在什么范围内,学生的接受能力逐步降低?
(2)第10 分钟时,学生的接受能力是多少?几分钟时,学生的接受能力最强? 思考:2.已知抛物线y=ax2+bx+c的图象如图所示,
下列结论:
①a+b+c<0 ②a-b+c>0 ③acb>0 ④b=2a,
其中正确的结论的个数是 ( )
A.4 B.3 C.2 D.1
当a﹤0时,开口 ,
2.对称轴是 ;
3.顶点坐标是 。向上向下(-h,k)直线X=-h向上( 1 , -2 )向下向下( 3 , 7)( 2 , -6 )向上直线x=-3直线x=1直线x=3直线x=2( -3, 5 )练习:注意函数y=2(x+3)2+5其实就是函数y=2x2+12x +23函数y = -3(x-1)2 -2其实就是函数y=-3x2+6x -5…..倒过来函数y=2x2+12x +23其实就是函数y=2(x+3)2+5函数y=-3x2+6x -5其实就是函数y = -3(x-1)2 -2二次函数y=3x2-6x+5的图象是什么形状?它与我们已经作过的二次函数的图象有什么关系?你用什么方法来研究它? 函数y=ax2+bx+c(二次函数的一般式)的图象 你能用配方的方法把y=3x2-6x+5变形成
y=a(x+m)2+k的形式吗?y=3x2-6x+5=3(x-1)2+2它的顶点坐标是 ,
对称轴是 . 总结:一般地,求形如y=ax2+bx+c的顶点及对称轴,我们可以用配方的方法。 y=-2x2-4x+3的顶点坐标是____ y=2x2+bx+c的顶点坐标是(1,-2),求b,c想一想: 你能说出函数y=ax2+bx+c(a≠0)的对称轴和它的顶点坐标最值吗?
函数y=ax2+bx+c经过配方变形后,可化为:y你能说出它的最值情况吗?1、写出下列抛物线的开口方向、对称轴及顶点坐标,当x为何值时y的值最大(小)? ?(1)y=3x2+2x(2)y=-x2-2x(3)y=-2x2+8x-8练习:3、若一次函数y=-2x+c与二次函数y=ax2 +bx-4
的图象都经过点A(1,-1),二次函数的对称轴直线
是x=-1,请求出一次函数和二次函数的表达式. 2、当m=___时,抛物线y=mx2 +2(m+2)x+m+3的
对称轴是y轴;
当m=_____时,图象与y轴交点的纵坐标是1;
当m=_____时,函数的最小值是-2. 4.写出一个二次函数的解析式,使它的顶点在第二象限且开口向下(要求用一般式表示)求y=x2+2x-8与坐标轴的交点。根据图象回答
何时y<0?
何时y>0?考点训练1、已知二次函数y=ax2+bx+c的图象如图所示
(1)求解析式
(2)何时 y=3?
(3)根据图象回答:
当x 时,y>0。2.如图,在同一坐标系中,函数y=ax+b与y=ax2+bx(ab≠0)的图象只可能是( ) 3.用总长为60m的篱笆墙围成矩形场地,矩形面积S随矩形一边长L的变化而变化,当L多少时,场地的面积S最大? 1.心理学家发现,学生对概念的接受能力y与提出:
概念所用的时间x(分钟)之间满足函数关系:
y=-0.1x2 +2.6x+43(0≤x≤30),y值越大表示接受能力越强.
(1)x在什么范围内,学生的接受能力逐步增加?x在什么范围内,学生的接受能力逐步降低?
(2)第10 分钟时,学生的接受能力是多少?几分钟时,学生的接受能力最强? 思考:2.已知抛物线y=ax2+bx+c的图象如图所示,
下列结论:
①a+b+c<0 ②a-b+c>0 ③acb>0 ④b=2a,
其中正确的结论的个数是 ( )
A.4 B.3 C.2 D.1
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
