§2-8 二次函数与一元二次方程(2)一元二次方程的图象解法[下学期]
文档属性
| 名称 | §2-8 二次函数与一元二次方程(2)一元二次方程的图象解法[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 320.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-23 00:00:00 | ||
图片预览






文档简介
课件15张PPT。九年级数学(下)
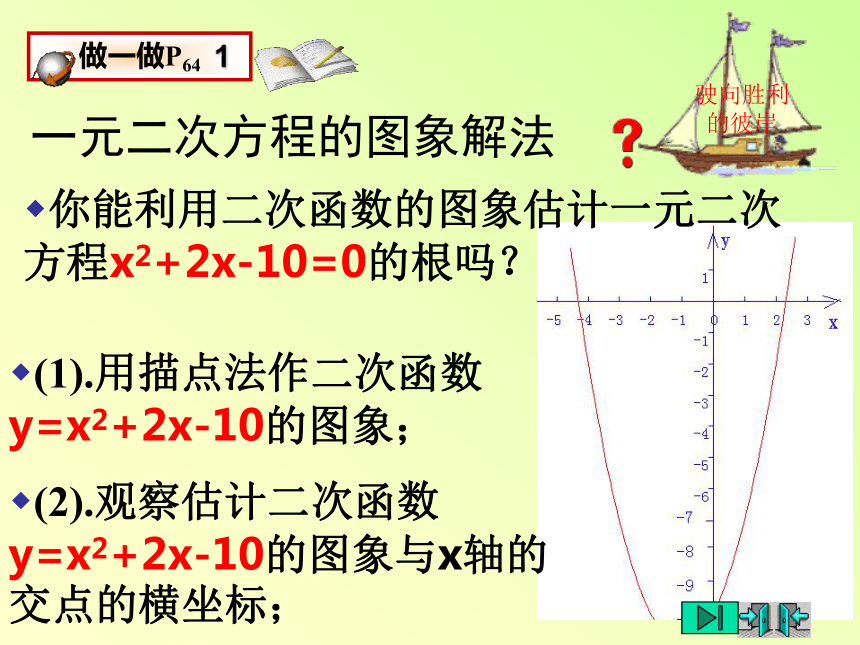
二次函数8. 二次函数与一元二次方程(2)一元二次方程的图象解法(1).用描点法作二次函数y=x2+2x-10的图象;一元二次方程的图象解法 你能利用二次函数的图象估计一元二次方程x2+2x-10=0的根吗?驶向胜利的彼岸(2).观察估计二次函数y=x2+2x-10的图象与x轴的交点的横坐标;由图象可知,图象与x轴有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.3和2.3(可将单位长再十等分,借助计算器确定其近似值,详见课本).(3).确定方程x2+2x-10=0的解;由此可知,方程x2+2x-10=0的近似根为:x1≈-4.3,x2≈2.3.(1).用描点法作二次函数y=x2+2x-10的图象;一元二次方程的图象解法 利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.驶向胜利的彼岸(2).观察估计抛物线y=x2+2x-10和直线y=3的交点的横坐标;(2). 作直线y=3;由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7(可将单位长再十等分,借助计算器确定其近似值).(3).确定方程x2+2x-10=3的解;由此可知,方程x2+2x-10=3的近似根为:x1≈-4.7,x2≈2.7.(1).原方程可变形为x2+2x-13=0;一元二次方程的图象解法 利用二次函数的图象求一元二次方程x2+2x-10=3的近似根.驶向胜利的彼岸(2).观察估计抛物线y=x2+2x-13和x轴的交点的横坐标;(2).用描点法作二次函数y=x2+2x-13的图象;;由图象可知,它们有两个交点,其横坐标一个在-5与-4之间,另一个在2与3之间,分别约为-4.7和2.7(可将单位长再十等分,借助计算器确定其近似值).(3).确定方程x2+2x-10=3的解;由此可知,方程x2+2x-10=3的近似根为:x1≈-4.7,x2≈2.7.一元二次方程的图象解法利用二次函数的图象求一元二次方程-2x2+4x+1=0的近似根.驶向胜利的彼岸(1).用描点法作二次函数y=-2x2+4x+1的图象;(2).观察估计二次函数y=-2x2+4x+1的图象与x轴的交点的横坐标;由图象可知,图象与x轴有两个交点,其横坐标一个在-1与0之间,另一个在2与3之间,分别约为-0.2和2.2(可将单位长再十等分,借助计算器确定其近似值).(3).确定方程-2x2+4x+1=0的解;由此可知,方程-2x2+4x+1=0的近似根为:x1≈-0.2,x2≈2.2.一元二次方程的图象解法利用二次函数的图象求一元二次方程2x2+x-15=0的近似根.驶向胜利的彼岸(1).用描点法作二次函数y=2x2+x-15的图象;(2).观察估计二次函数y=2x2+x-15的图象与x轴的交点的横坐标;由图象可知,图象与x轴有两个交点,其横坐标一个是-3,另一个在2与3之间,分别约为3和2.5(可将单位长再十等分,借助计算器确定其近似值).(3).确定方程2x2+x-15=0的解;由此可知,方程2x2+x-15=0的近似根为:x1≈-3,x2≈2.5.一元二次方程的图象解法利用二次函数的图象求一元二次方程3x2-x-1=0的近似根.驶向胜利的彼岸(1).用描点法作二次函数y=3x2-x-1的图象;(2).观察估计二次函数y=3x2-x-1的图象与x轴的交点的横坐标;由图象可知,图象与x轴有两个交点,其横坐标一个在-1与0之间,另一个在0与1之间,分别约为-0.4和0.8(可将单位长再十等分,借助计算器确定其近似值).(3).确定方程3x2-x-1=0的解;由此可知,方程3x2-x-1=0的近似根为:x1≈-0.4,x2≈0.8.知识的升华P72 习题2.9 1题.
祝你成功!结束寄语不知道并不可怕和有害,任何人都不可能什么都知道,可怕的和有害的是不知道而伪装知道.
祝你成功!结束寄语不知道并不可怕和有害,任何人都不可能什么都知道,可怕的和有害的是不知道而伪装知道.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
