7.3 特殊角的三角函数[下学期]

课件27张PPT。特殊角的三角函数值Everyone,欢迎进入奇妙的数学世界！特殊角的三角函数值回顾
旧知学以
致用感悟
反思课堂
总结布置
作业学习
目标探求
新知 学习目标
1、能根据正弦、余弦、正切、余切的定义，求出30°、45°、60°角的三角函 数值。
2、熟记30°、45°、60°角的三角函 数值。
3、能运用三角函数解决可以转化为直角三角形问题的简单的实际问题。特殊角三角函数值直角三角形的两个锐角之间有什么关系?直角三角形的两个锐角互余。知 识回 顾知 识回 顾 射影定理
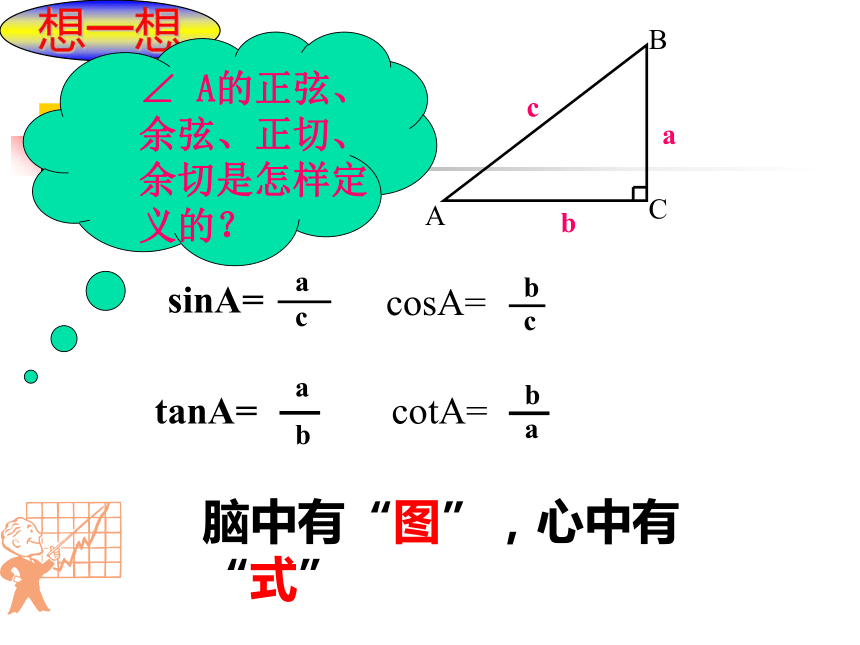
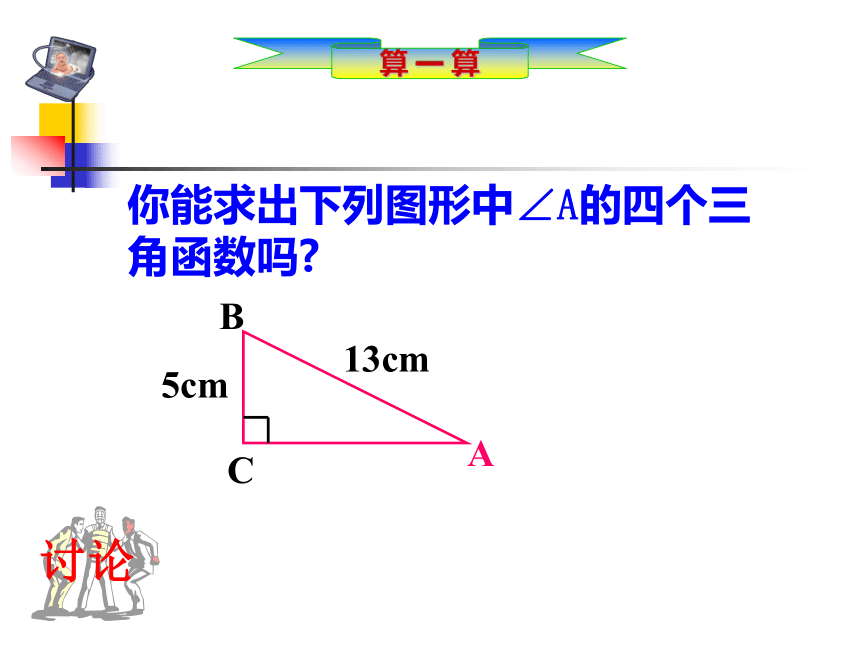
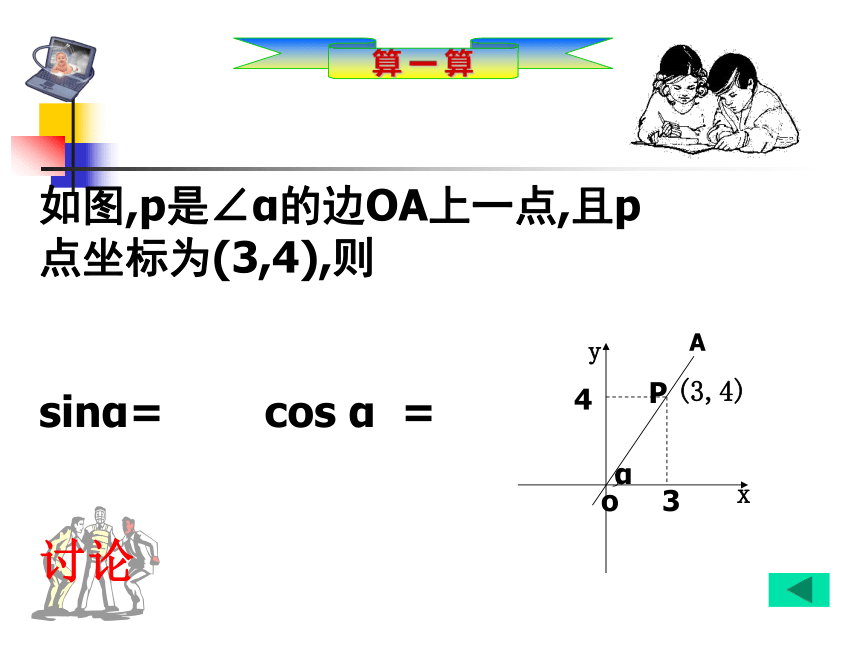
想一想abcsinA=cosA=tanA=cotA=脑中有“图”，心中有“式”算 一 算讨论你能求出下列图形中∠A的四个三角函数吗?算 一 算讨论如图,p是∠α的边OA上一点,且p点坐标为(3,4),则

sinα= cos α =
αA做一做12成功就在你面前sin30°=
cos30°=
tan30°=
cot30°=?30011成功就在你面前Sin45　=
cos45°=
tan45°=
cot45°=11做一做12成功就在你面前sin60°=
cos60°=
tan60°=
cot60°=做一做角α三角函数11填一填 记一记做一做成功就在你面前1、sin30°+cos60°=2、sin60°-tan45°=3、tan60°-cos30°=4、tan45°-sin30°=做一做　　已知∠A为锐角，且cosA= ，
你能求出∠A的度数吗。讨论想一想我能行(1) sin30°+cos45°(2) sin260°+cos260°-tan45°看谁做的快！行！
我肯定行！
某商场有一自动扶梯，其倾斜角为３0°, 高为7米,扶梯的长度是多少?成功就在你面前一根4米长的竹竿，斜靠在墙上。请问： 1、如果竹竿与地面成60°的角，角多远？那么竹竿下端离墙2、如果竹竿上端顺墙下滑到高度2米处停止，那么此时竹竿与地面成锐角的大小是多少？
? 问题征答嗨，你真棒！ 已知方程x2-7x+12=0的两根为一个直三角形的两条直角边,求较小角的余弦值.
问 题 探 讨 等腰三角形腰长为10厘米，顶角是120°，则三角形底 边长 ， 面积是 。
探究无止境 认真观察一下特殊角三角函数值表格
你能发现什么规律？读 一 读 “三角学”一词源于希腊文的“三角形”与“测量”，原意是“三角形的测量”。后来人们把利用三角函数研究三角形和其他图形的数量关系,进而研究三角函数的性质及其应用的数学学科称为三角学.
三角学的发展大致可分为三个时期。从远古至11世纪前为第一个时期。再此期间，虽然人们还没有明确提到三角形的边与角之间的数量关系，更没有角的函数的概念，但是人们已经能够利用当时掌握的数学知识解决属于三角学范围内的一些实际问题。
11到18世纪是三角学发展的第二个时期。这一时期，由于测量、贸易和航海等方面的需要，三角学得到了迅速发展，并逐步形成一门独立的数学学科。再此期间，人们编制出大量的三角函数表，三角得到广泛应用。
开眼界？读 一 读 第三个时期是18世纪以后，这时三角学的研究逐步演变为研究三角函数的性质与应用，而且引进了现在所使用的三角函数符号。
三角学输入我国，开始于明朝崇祯四年（1631）。这一年邓玉函、汤若望、徐光启（1562---1633）合编了《大测》，这是我国第一部三角学著；徐光启等人编写了《测量全义》。1877年华衡芳（1833---1902）与英国人傅兰雅合译英国人海麻士的《三角数理》，这是三角学第二次输入我国。开眼界？请你谈谈对本节学习内容的体会和感受。
作业：
48页习题1、2
课外探究 在数学活动课上，老师带领同学们去测小河宽。在A处用测角器测得∠DAC=60。然后沿DA方向前进30米至B处，测得∠DBC=30。试问：依据同学们所测得数据，能否求出小河的宽度CD的值呢？如果可以，请你求出小河的宽度；如果不行，请说明理由。CDAB3030°60°谢谢各位老师光临指导!