二次根式的乘除(2)[上学期]
图片预览





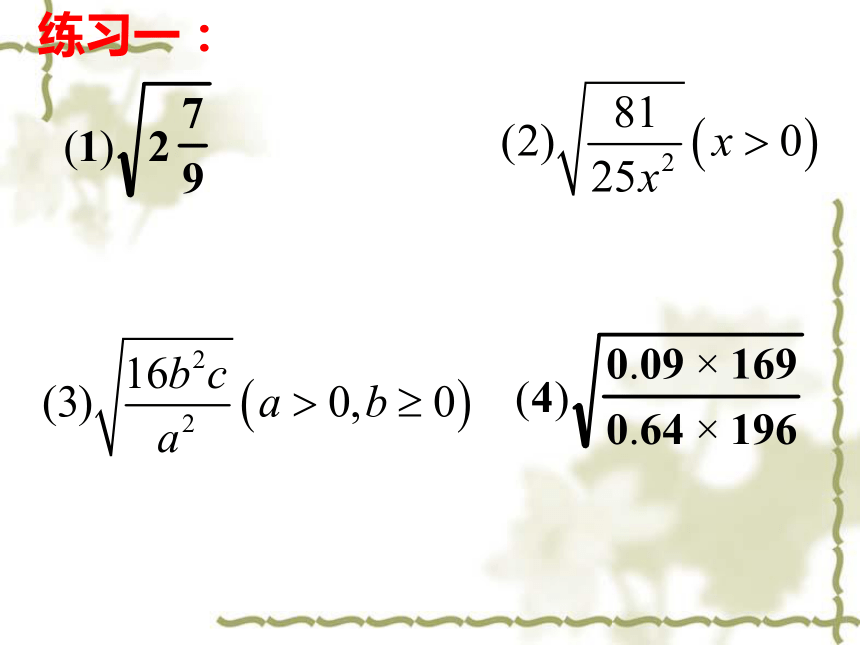
文档简介
课件14张PPT。二次根式的乘法 注意:
a、b 必须都是非负数,上式才能成立。复习回顾二次根式的乘法公式积的算术平方根的性质能力提高题二次根式的除法二. 探究新知:二次根式的除法1、二次根式的除法:
(1)数学表达式:一. 引入:判断(1)、(2)的关系。计算:(2)语言叙述: 两个二次根式相除,等于
把被开方数相除,根指数不变。三. (1)商的算术平方根:(1)数学表达式:(2)语言叙述:商的算术平方根等于
被除式的算术平方根除以除式的算术平方根。2、商的算术平方根的性质的应用
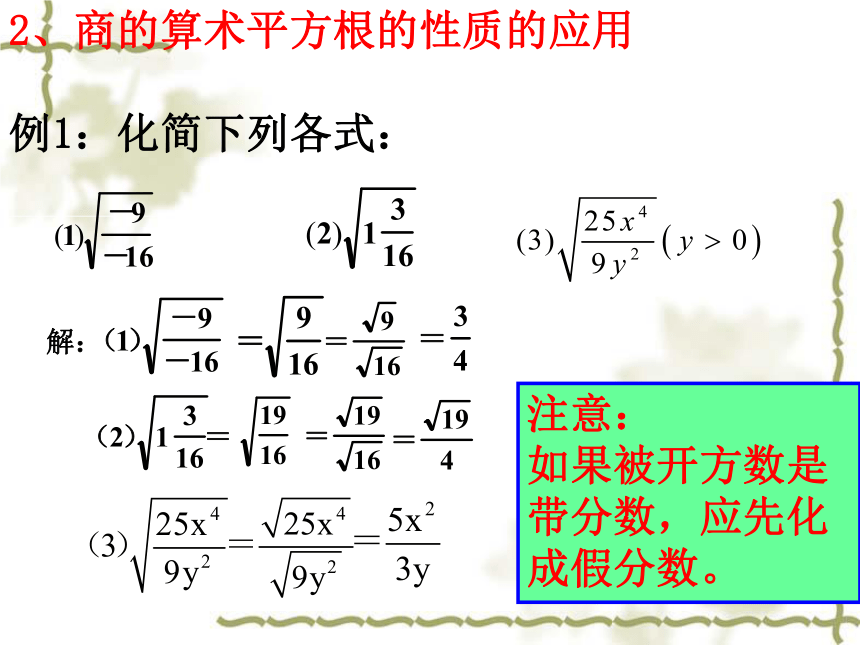
例1:化简下列各式:
注意:
如果被开方数是带分数,应先化成假分数。解:练习一:4. 二次根式的除法公式的应用:例2. 计算:
解:如果根号前有系数,就把系数相除,仍旧作为二次根号前的系数。注意:
利用 求二次根式的商有一定的局限性,它只适用于被除式与除式的被开方数恰为能整除的形式,如:5. 分母有理化的概念:
把分母中的根号化去,使分母变成有理数,这个过程叫做分母有理化。
如果遇有不能整除的情况怎么办呢?例如:
通常我们是采用化去分母中根号的方法来进行的。这就是我们要讲的分母有理化。练习:把下列各式的分母有理化:
注意:要进行根式化简,关键是要搞清楚分式的分子和分母都乘什么,有时还要对分母进行化简。1.被开方数不含分母且分母中不含根号2.被开方数不含开的尽方的因数或因式最简二次根式1.在横线上填写适当的数或式子使等式成立。练习二:2.把下列各式的分母有理化:3.化简:( )( )= a-1( )= 10( )= 41. 利用商的算术平方根的性质化简二次根式。课堂小结:3. 在进行分母有理化之前,可以先观察把能化简的二次根式先化简,再考虑如何化去分母中的根号。2. 二次根式的除法有两种常用方法:(1)利用公式:(2)把除法先写成分式的形式,再进行分母有理化运算。思考题:
a、b 必须都是非负数,上式才能成立。复习回顾二次根式的乘法公式积的算术平方根的性质能力提高题二次根式的除法二. 探究新知:二次根式的除法1、二次根式的除法:
(1)数学表达式:一. 引入:判断(1)、(2)的关系。计算:(2)语言叙述: 两个二次根式相除,等于
把被开方数相除,根指数不变。三. (1)商的算术平方根:(1)数学表达式:(2)语言叙述:商的算术平方根等于
被除式的算术平方根除以除式的算术平方根。2、商的算术平方根的性质的应用
例1:化简下列各式:
注意:
如果被开方数是带分数,应先化成假分数。解:练习一:4. 二次根式的除法公式的应用:例2. 计算:
解:如果根号前有系数,就把系数相除,仍旧作为二次根号前的系数。注意:
利用 求二次根式的商有一定的局限性,它只适用于被除式与除式的被开方数恰为能整除的形式,如:5. 分母有理化的概念:
把分母中的根号化去,使分母变成有理数,这个过程叫做分母有理化。
如果遇有不能整除的情况怎么办呢?例如:
通常我们是采用化去分母中根号的方法来进行的。这就是我们要讲的分母有理化。练习:把下列各式的分母有理化:
注意:要进行根式化简,关键是要搞清楚分式的分子和分母都乘什么,有时还要对分母进行化简。1.被开方数不含分母且分母中不含根号2.被开方数不含开的尽方的因数或因式最简二次根式1.在横线上填写适当的数或式子使等式成立。练习二:2.把下列各式的分母有理化:3.化简:( )( )= a-1( )= 10( )= 41. 利用商的算术平方根的性质化简二次根式。课堂小结:3. 在进行分母有理化之前,可以先观察把能化简的二次根式先化简,再考虑如何化去分母中的根号。2. 二次根式的除法有两种常用方法:(1)利用公式:(2)把除法先写成分式的形式,再进行分母有理化运算。思考题:
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
