二次根式的乘除(2).[上学期]
图片预览


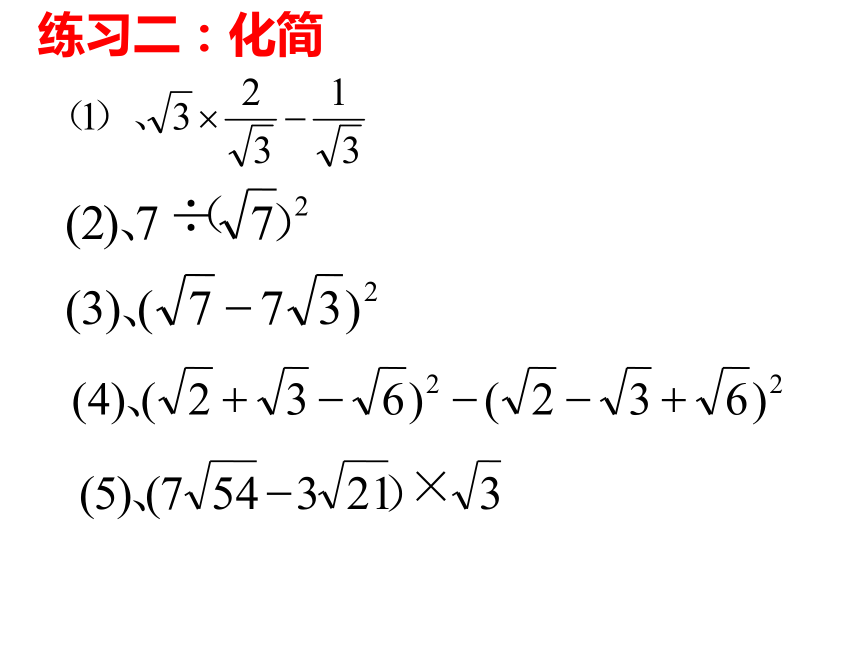



文档简介
课件17张PPT。 二次根式的除法语言叙述: 两个二次根式相除,等于
把被开方数相除,根指数不变。商的算术平方根:语言叙述:商的算术平方根等于被除式的
算术平方根除以除式的算术平方根。练习一:化简练习二:化简注意:
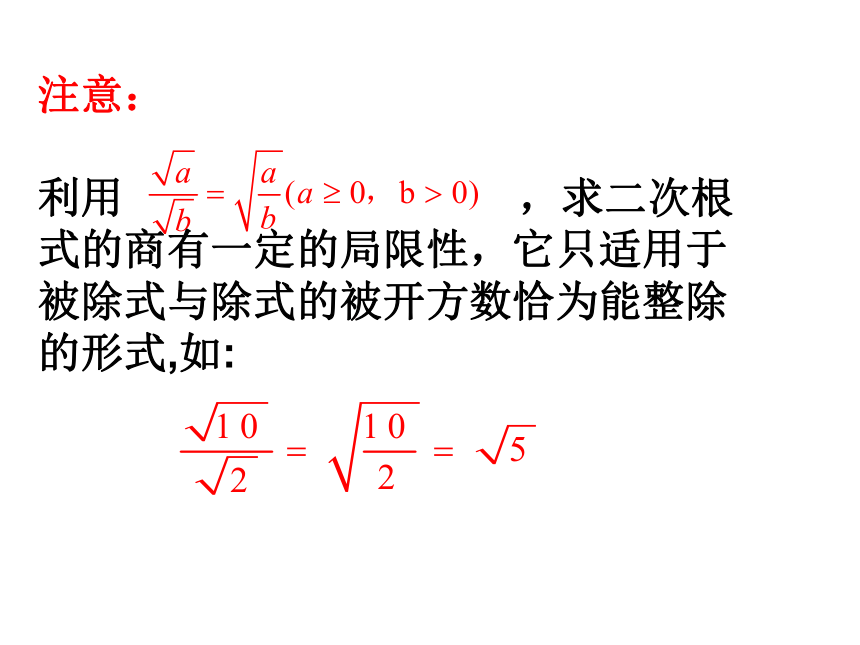
利用 ,求二次根式的商有一定的局限性,它只适用于被除式与除式的被开方数恰为能整除的形式,如:如果遇有不能整除的情况怎么办呢?例如:
通常我们是采用化去分母中根号的方法来进行的。这就是我们要讲的分母有理化。分母有理化 平方差公式在整式中成立,它在二次根式中是否成立呢?请你计算下列式子: 两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们说这两个代数式互为有理化因式。 你能否举出几个互为有理化因式的例子?分母有理化:1、定义:把分母中的根号化去。2、方法:分子、分母同时乘以分母的有理化因式。3、常见的互为有理化因式:的有理化因式:练习:把下列各式的分母有理化:
注意:要进行根式化简,关键是要搞清楚分式的分子和分母都乘什么,有时还要对分母进行化简。1.被开方数不含分母且分母中不含根号2.被开方数不含开的尽方的因数或因式最简二次根式1.在横线上填写适当的数或式子使等式成立。练习二:2.把下列各式的分母有理化:3.化简:( )( )= a-1( )= 10( )= 4 怎样把下面的代数式分母有理化?例1 把下列各式分母有理化:例2 计算:(黄石市,2000)甲、乙两同学对代数式分别作了如下变形:甲:乙:你怎样看待它们的变形呢?小结1、会利用分母有理化进行二次根式的除法运算。2、会用较简便的方法将含有二次根式的式子分母有理化。3、从中体会简化的思想方法。思考题:
把被开方数相除,根指数不变。商的算术平方根:语言叙述:商的算术平方根等于被除式的
算术平方根除以除式的算术平方根。练习一:化简练习二:化简注意:
利用 ,求二次根式的商有一定的局限性,它只适用于被除式与除式的被开方数恰为能整除的形式,如:如果遇有不能整除的情况怎么办呢?例如:
通常我们是采用化去分母中根号的方法来进行的。这就是我们要讲的分母有理化。分母有理化 平方差公式在整式中成立,它在二次根式中是否成立呢?请你计算下列式子: 两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们说这两个代数式互为有理化因式。 你能否举出几个互为有理化因式的例子?分母有理化:1、定义:把分母中的根号化去。2、方法:分子、分母同时乘以分母的有理化因式。3、常见的互为有理化因式:的有理化因式:练习:把下列各式的分母有理化:
注意:要进行根式化简,关键是要搞清楚分式的分子和分母都乘什么,有时还要对分母进行化简。1.被开方数不含分母且分母中不含根号2.被开方数不含开的尽方的因数或因式最简二次根式1.在横线上填写适当的数或式子使等式成立。练习二:2.把下列各式的分母有理化:3.化简:( )( )= a-1( )= 10( )= 4 怎样把下面的代数式分母有理化?例1 把下列各式分母有理化:例2 计算:(黄石市,2000)甲、乙两同学对代数式分别作了如下变形:甲:乙:你怎样看待它们的变形呢?小结1、会利用分母有理化进行二次根式的除法运算。2、会用较简便的方法将含有二次根式的式子分母有理化。3、从中体会简化的思想方法。思考题:
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
