直角三角形全等的判定（二）[上学期]

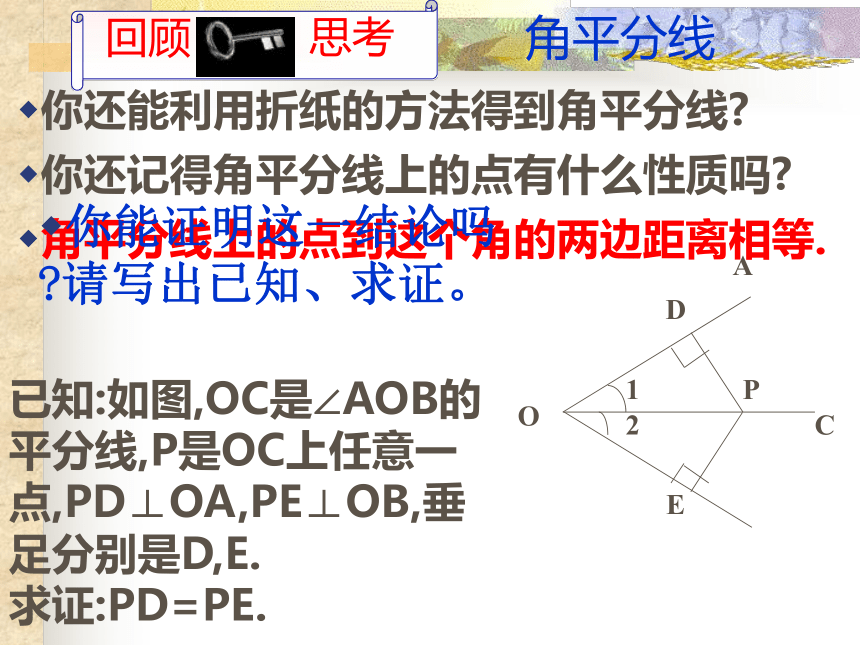
课件23张PPT。直角三角形全等的判定（二）角平分线你还能利用折纸的方法得到角平分线?已知:如图,OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E.
求证:PD=PE.你还记得角平分线上的点有什么性质吗?角平分线上的点到这个角的两边距离相等.你能证明这一结论吗?请写出已知、求证。几何的三种语言定理 角平分线上的点到这个角的两边距离相等.
老师提示:这个结论是经常用来证明两条线段相等的根据之一.注意定理的几何语言的描述：
∵OC是∠AOB的平分线,P是OC上一点,PD⊥OA,PE⊥OB,垂足分别是D,E(已知)
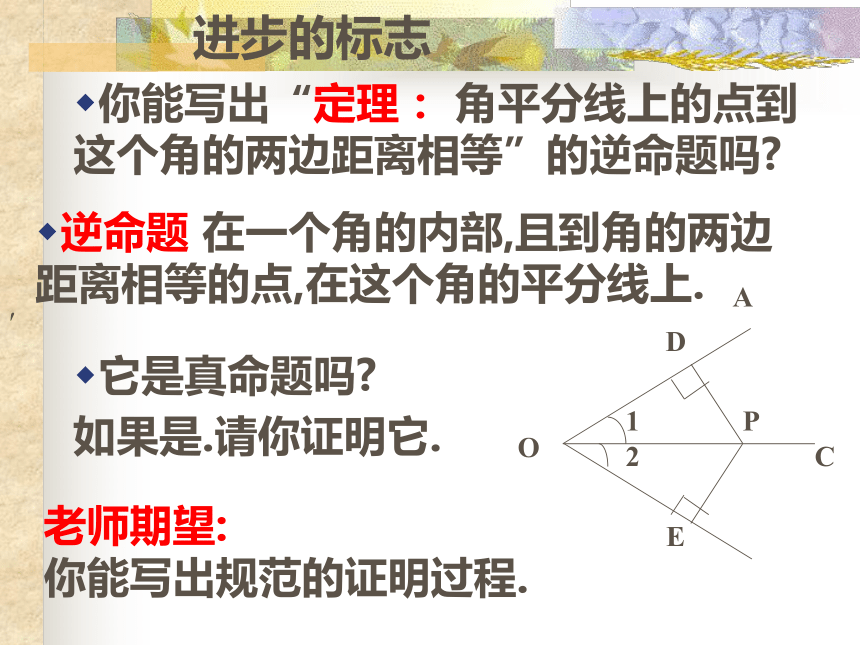
∴PD=PE(角平分线上的点到这个角的两边距离相等).进步的标志′你能写出“定理： 角平分线上的点到这个角的两边距离相等”的逆命题吗?
逆命题 在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.它是真命题吗?如果是.请你证明它.老师期望:
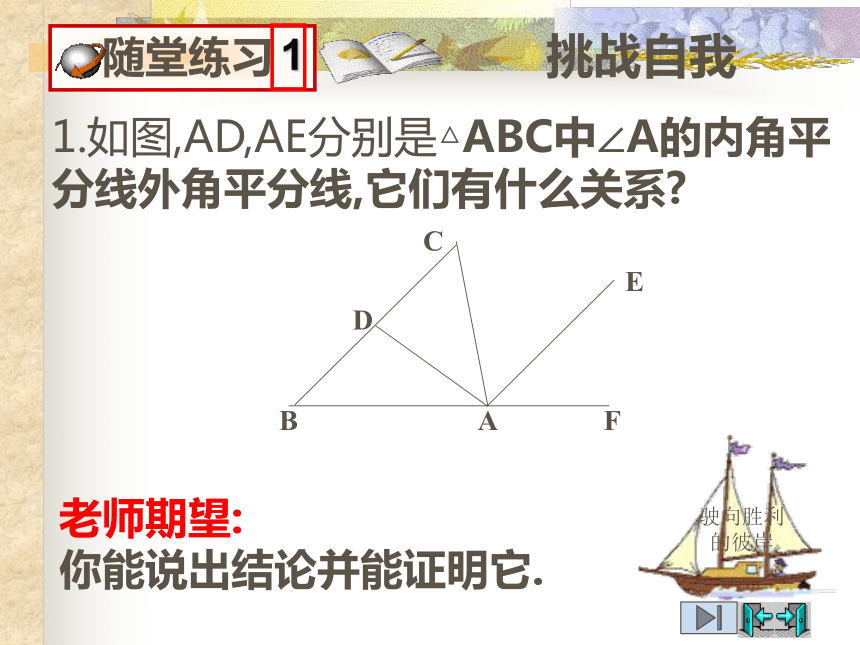
你能写出规范的证明过程.逆定理逆定理 在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.注意：如何用几何语言的描述这个逆定理？老师提示:这个结论又是经常用来证明点在角平分线上(或直线经过某一点)的根据之一.从这个结果出发,你还能联想到什么?思考：“如果一个点到角的两边距离不相等，那么这个点不在这个角平分线上”这句话对吗？挑战自我1.如图,AD,AE分别是△ABC中∠A的内角平分线外角平分线,它们有什么关系?老师期望:
你能说出结论并能证明它.梦想成真2.如图,一目标在A区,到期公路,铁路距离相等,离公路与铁路的交叉处500m.在图上标出它的位置(比例尺 1:20 000).3.利用尺规作出三角形三个内角的平分线. 老师期望:
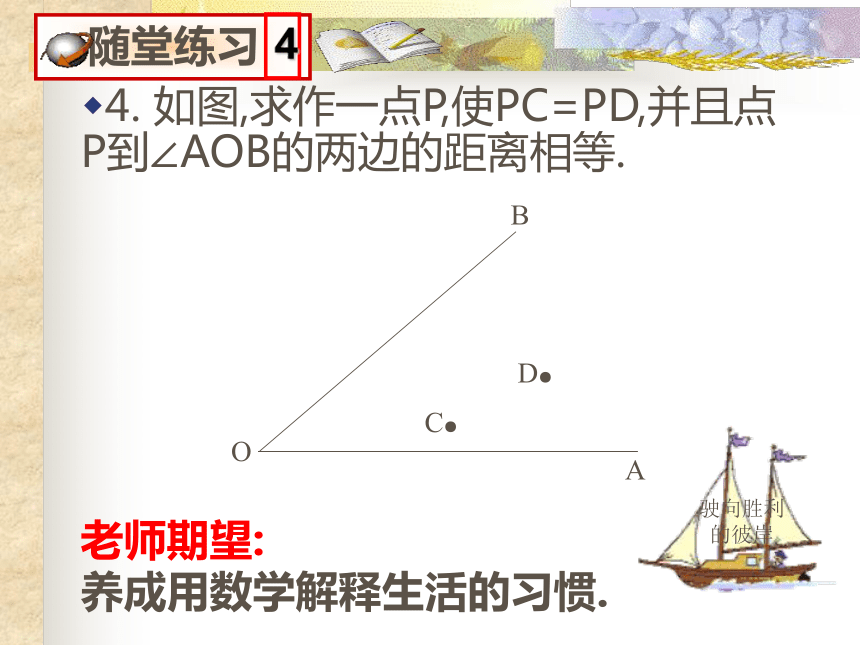
先分别作出不同形状的三角形,再按要求去作图.你发现了什么？你你得到了什么结论？4. 如图,求作一点P,使PC=PD,并且点P到∠AOB的两边的距离相等. 老师期望:
养成用数学解释生活的习惯. 5.已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC. 老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去. 6.如图Rt △ABC中，C=90，BC=16cm,AD是△BAC的角平分线，交BC于D，且BD：DC=5：3，求点D到AB的距离.7.三条铁路两两相交,如图所示,欲建一个客运站,使客运站到三条铁路线的距离都相等,试问客运站应建在什么位置,你能画出来吗?六、已知等腰Δ ABC的底边为AB，直线l过直角顶点C，过点A、B分别作l的垂线AE、BF，E、F两点为垂足。
（1）如图1，当直线l不与AB相交时，求证：EF=AE+BF六、已知等腰Δ ABC的底边为AB，直线l过直角顶点C，过点A、B分别作l的垂线AE、BF，E、F两点为垂足。
（2）将直线l绕点C顺时针旋转，使l交底边AB于点D，且AD>BD,请先画图,再写出EF、AE、BF之间的关系。1.已知:如图,在△ABC中，BO、CO分别平分∠ABC、∠ACB并交于点O,过点O作 OD∥AB, OE∥AC,BC=16,
求: △ODE的周长2.请把这个三角形纸片折成两个等腰三角形！1、对∠A进行讨论2、对∠B进行讨论3、对∠C进行讨论（分类讨论） 3：如图，AD是△ABC的角平分线AB=AC+DC，求证：∠C=2∠BABCDE变：如图，在△ABC中AD⊥BC于D、AB+DB=DC，求证：∠B=2∠C
ABCDE4：如图，AB＞AC，AD是角平分线，E是AB上的一点，AE=AC，EF∥BC交AC于F，求证：CE平分∠DEFABCDEF5.（1）如图1，等边△ABC中，D是AB上的一动点，以CD为一边向上作等边△EDC，连AE，
求证：AE∥BC
（2）如图2，将（1）中等边△ABC改为以BC为底边的等腰三角形所作△EDC改为相似于△ABC，请问：是否仍有AE∥BC？证明你的结论。ABCDE图1ABCED图2 6.如图，点C为线段AB上的一点△ACM，△CBN是等边三角形线段AN、CM相交于点E，线段BM、CN相交于点F。（1）求证：AN=BM
（2）△CEF是等边三角形
（3）将△ACM绕点C逆时针方向旋转900 ，在图2中补出符合条件的的图形，并判断（1）（2）两题的结论是否仍然成立，证明你的结论。ABCMNEFABCMN练一练7、在△ABC中，∠ACB＝90°，CD⊥AB于D，AE平分∠BAC交BC于E，交CD于F，FG∥AB交BC于G。求证：1、CE=CF 2、CG=EB