1.2直角三角形全等的判定1[上学期]
文档属性
| 名称 | 1.2直角三角形全等的判定1[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 369.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-10-21 00:00:00 | ||
图片预览



文档简介
课件13张PPT。 1.2 直角三角形全 等的判定1、我们已经证明过的判定两个三角形全等的方法有:
、 、 、 。SSSASAAASSAS2、判定两个直角三角形全等除了上面的方法外,还有其它的方法吗?思考探索
定理 斜边和一条直角边对应相等的两个直角三角形全等.
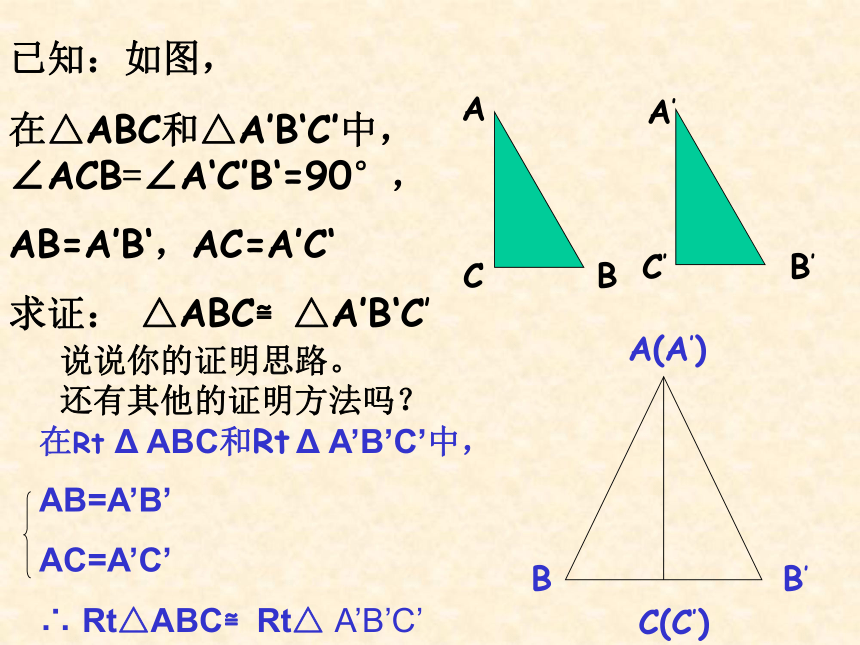
简写成“斜边、直角边”或“HL”.你能证明这个结论吗?已知:如图,
在△ABC和△A’B‘C’中,∠ACB=∠A‘C’B‘=90°,
AB=A’B‘,AC=A’C‘
求证: △ABC≌△A’B‘C’说说你的证明思路。
还有其他的证明方法吗?在Rt Δ ABC和Rt Δ A’B’C’中,
AB=A’B’
AC=A’C’
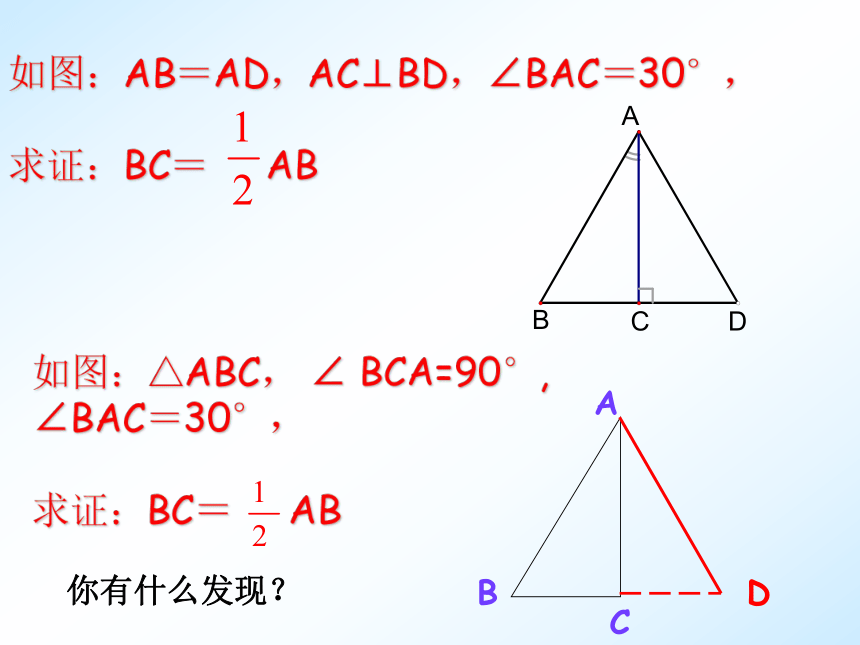
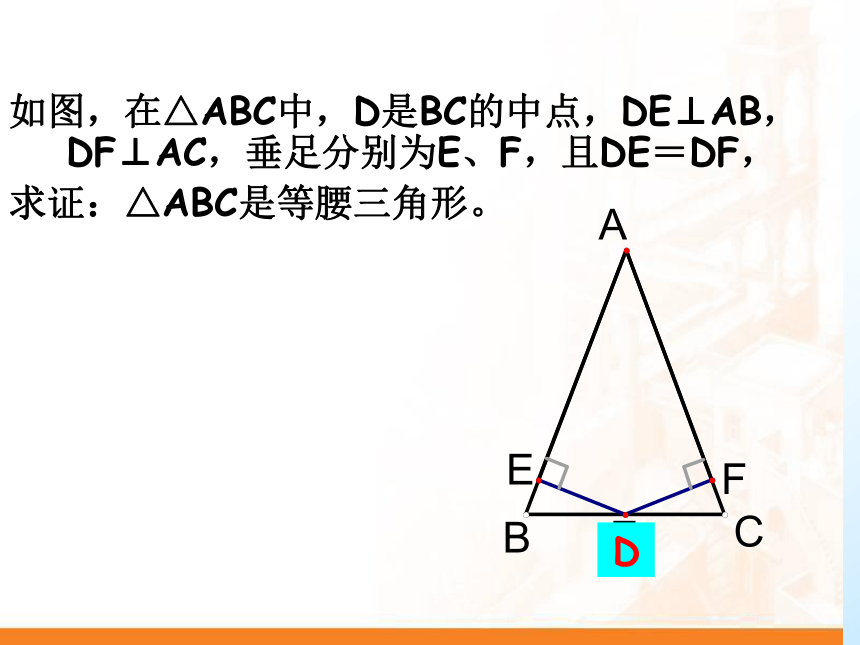
∴ Rt△ABC≌Rt△ A’B’C’ 如图:AB=AD,AC⊥BD,∠BAC=30°, 求证:BC= AB如图:△ABC, ∠ BCA=90°, ∠BAC=30°, 求证:BC= ABD你有什么发现?直角三角形30°角所对的直角边长等于斜边长的一半。直角三角形还有其他的性质吗?直角三角形斜边上的中线等于斜边的一半。如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,
求证:△ABC是等腰三角形。D如图AD⊥DB,BC⊥CA,AC、BD相交于点O,如果AD=BC,那么图中还有哪些相等的线断,请证明。已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于D,∠A=30°.
求证:BD= AB在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于E.
(1)若BC在DE的同侧(如图①)且AD=CE,说明:BA⊥AC.
(2)若BC在DE的两侧(如图②)其他条件不变,问AB与AC仍垂直吗?若是请予证明,若不是请说明理由. 一,下列判断对吗?并说明理由:1、两个锐角对应相等的两个直角三角形全等; 2、斜边及一个锐角对应相等的两个直角三角形全等;3、两直角边对应相等的两个直角三角形全等;4、一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等.回味无穷直角三角形全等的判定定理:
定理:斜边和一条直角边对应相等的两个直角三角形全等(斜边,直角边或HL).
公理:三边对应相等的两个三角形全等(SSS).
公理:两边及其夹角对应相等的两个三角形全等(SAS).
公理:两角及其夹边对应相等的两个三角形全等(ASA).
推论:两角及其中一角的对边对应相等的两个三角形全等(AAS).
综上所述,直角三角形全等的判定条件可归纳为:
一边及一个锐角对应相等的两个直角三角形全等;
两边对应相等的两个直角三角形全等;感悟与反思作业:作业本再见
、 、 、 。SSSASAAASSAS2、判定两个直角三角形全等除了上面的方法外,还有其它的方法吗?思考探索
定理 斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”或“HL”.你能证明这个结论吗?已知:如图,
在△ABC和△A’B‘C’中,∠ACB=∠A‘C’B‘=90°,
AB=A’B‘,AC=A’C‘
求证: △ABC≌△A’B‘C’说说你的证明思路。
还有其他的证明方法吗?在Rt Δ ABC和Rt Δ A’B’C’中,
AB=A’B’
AC=A’C’
∴ Rt△ABC≌Rt△ A’B’C’ 如图:AB=AD,AC⊥BD,∠BAC=30°, 求证:BC= AB如图:△ABC, ∠ BCA=90°, ∠BAC=30°, 求证:BC= ABD你有什么发现?直角三角形30°角所对的直角边长等于斜边长的一半。直角三角形还有其他的性质吗?直角三角形斜边上的中线等于斜边的一半。如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF,
求证:△ABC是等腰三角形。D如图AD⊥DB,BC⊥CA,AC、BD相交于点O,如果AD=BC,那么图中还有哪些相等的线断,请证明。已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于D,∠A=30°.
求证:BD= AB在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于E.
(1)若BC在DE的同侧(如图①)且AD=CE,说明:BA⊥AC.
(2)若BC在DE的两侧(如图②)其他条件不变,问AB与AC仍垂直吗?若是请予证明,若不是请说明理由. 一,下列判断对吗?并说明理由:1、两个锐角对应相等的两个直角三角形全等; 2、斜边及一个锐角对应相等的两个直角三角形全等;3、两直角边对应相等的两个直角三角形全等;4、一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等.回味无穷直角三角形全等的判定定理:
定理:斜边和一条直角边对应相等的两个直角三角形全等(斜边,直角边或HL).
公理:三边对应相等的两个三角形全等(SSS).
公理:两边及其夹角对应相等的两个三角形全等(SAS).
公理:两角及其夹边对应相等的两个三角形全等(ASA).
推论:两角及其中一角的对边对应相等的两个三角形全等(AAS).
综上所述,直角三角形全等的判定条件可归纳为:
一边及一个锐角对应相等的两个直角三角形全等;
两边对应相等的两个直角三角形全等;感悟与反思作业:作业本再见
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
