三角形的中位线[上学期]

N覊b_-NMO縹.ppt(共25张PPT)
姓名:许效宇
学校:赣榆县华杰双语学校
邮编:222100
B
D
A
E
C
F
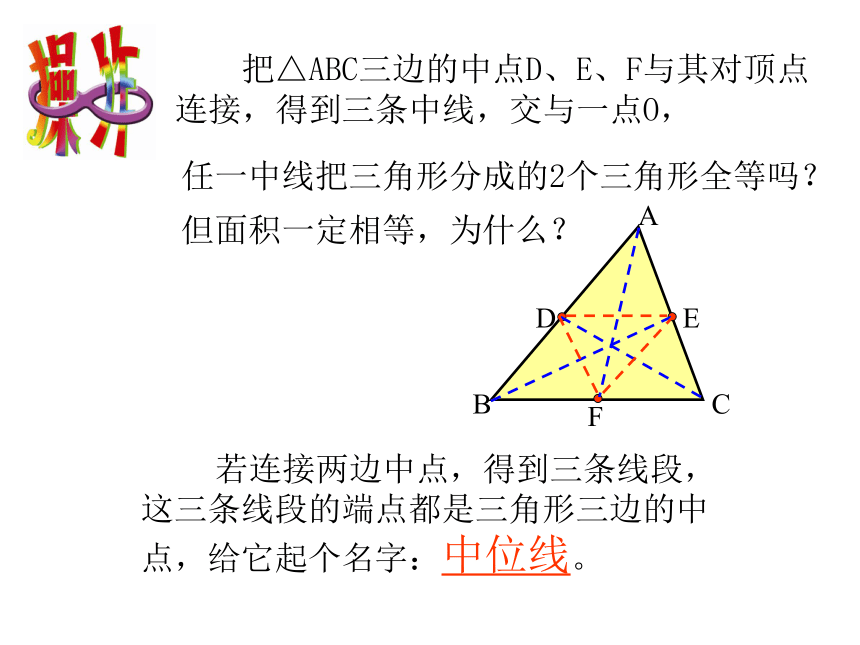
把△ABC三边的中点D、E、F与其对顶点连接，得到三条中线，交与一点O，
但面积一定相等，为什么？
若连接两边中点，得到三条线段，这三条线段的端点都是三角形三边的中点，给它起个名字：中位线。
任一中线把三角形分成的2个三角形全等吗？
B
D
A
E
C
F
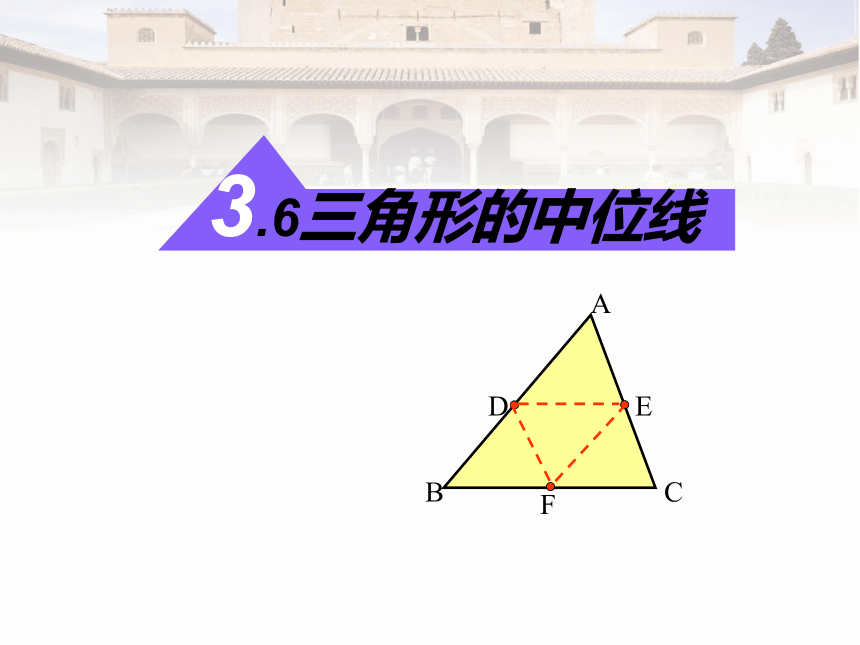
3.6三角形的中位线
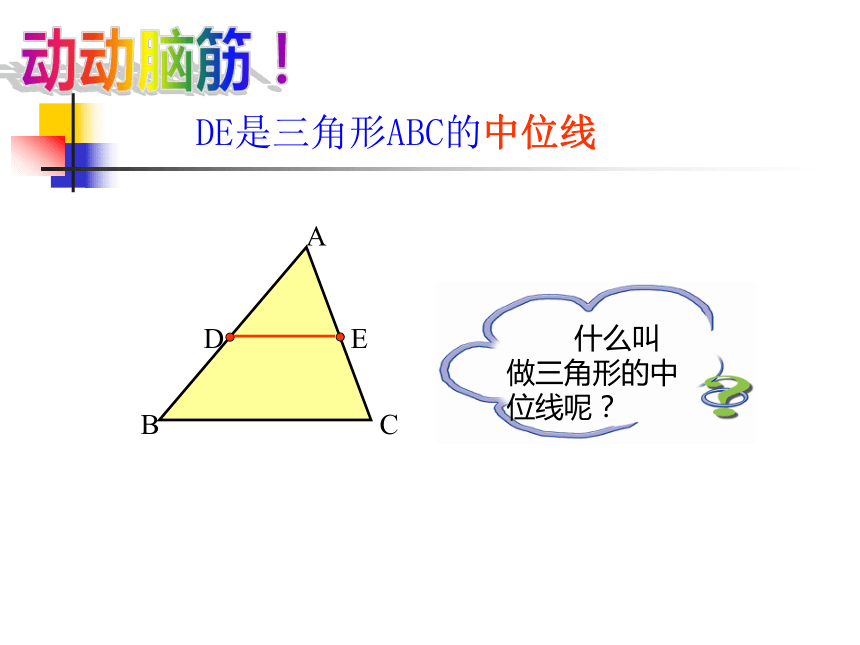
DE是三角形ABC的中位线
B
D
A
E
C
什么叫做三角形的中位线呢？
B
D
A
E
C
连接三角形两边中点的线段叫做三角形的中位线
图形语言
符号语言
∵D、E分别为AB、AC的中点
∴DE为△ABC的中位线
反之
若DE为△ABC的中位线
则 D、E分别为AB、AC的中点
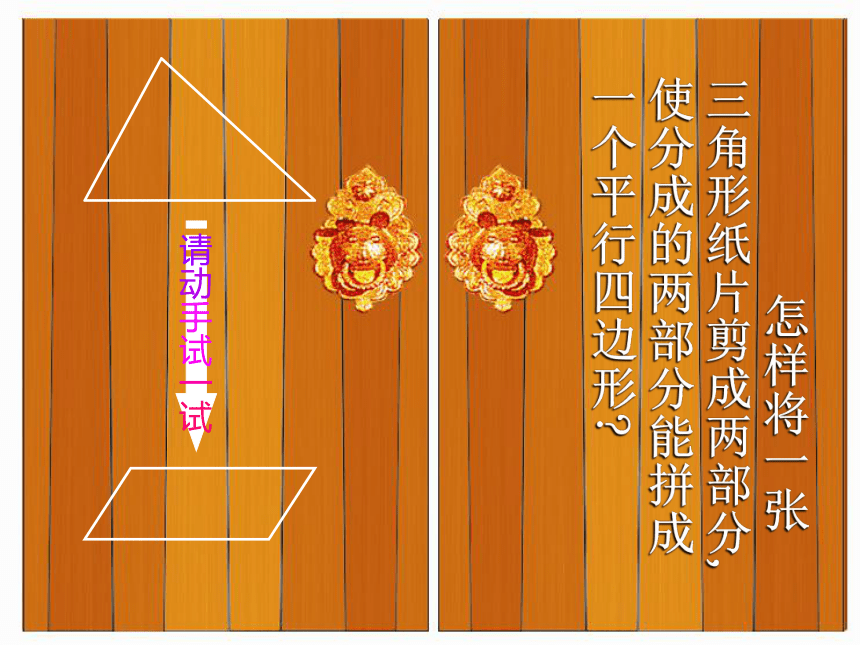
怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形
请动手试一试
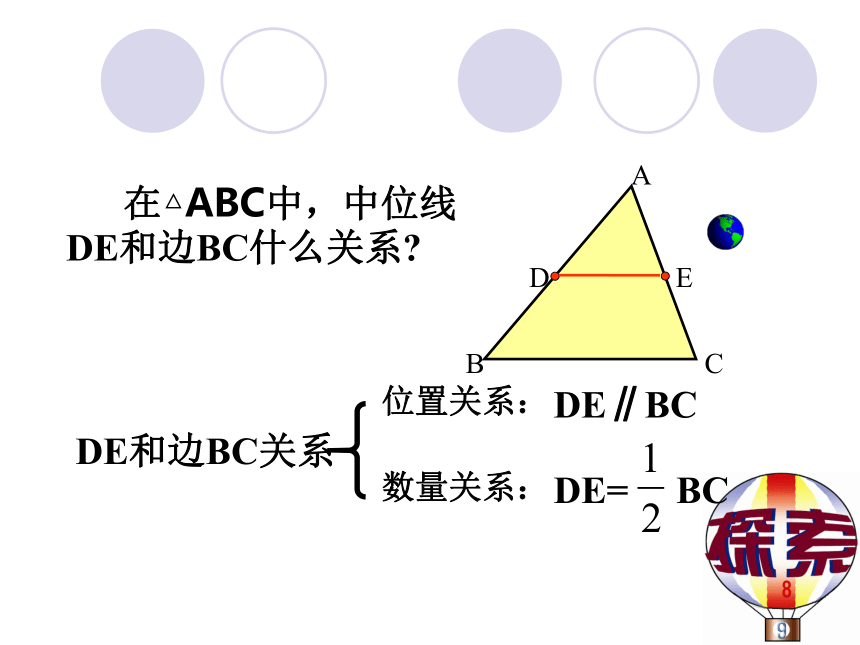
在△ABC中，中位线DE和边BC什么关系
DE和边BC关系
数量关系：
位置关系：
DE∥BC
DE= BC
B
D
A
E
C
三角形的中位线平行于第三边，并且等于它的一半.
B
D
A
E
C
用符号语言表示
∵DE是△ABC的中位线
∴ DE∥BC，
DE= BC.
2
1
画出△ABC中所有的中位线
B
D
A
E
C
F
三条中位线围成一个新的三角形，它与原来的三角形有无关系 哪方面有关系
(1) △DEF的周长与 △ABC的周长有什么关系
(2) △DEF的面积与 △ABC的面积有什么关系
A
B
C
测出MN的长，就可知A、B两点的距离
M
N
在AB外选一点C，使C能直接到达A和B，
连结AC和BC，并分别找出AC和BC的中点M、N.
若MN=36 m，则AB=
2MN=72 m
如果，MN两点之间还有阻隔，你有什么解决办法？
如图A、B两地被池塘阻隔
例1、如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是平行四边形吗？为什么？
A
B
C
D
E
F
G
H
连接AC，
在△ABC中，
因为E、F分别是AB、BC边的中点，
即EF是△ABC的中位线.
所以EF//AC，EF= AC
理由是：三角形的中位线平行于第三边，并且等于他的一半．
同理可得：HG//AC，HG= AC
所以EF//HG，EF=HG
所以四边形EFGH是平行四边形
2
1
2
1
解：四边形EFGH是平行四边形.
从例1中你能得到什么结论？
顺次连接四边形各边中点的线段组成一个
顺次连接矩形各边中点的线段组成一个
菱形
平行四边形
如图，在矩形ABCD中，E、F、G、H分别是边AB、BC、CD、AD的中点，试说明四边形EFGH是菱形.
解：连接AC、BD
根据三角形中位线定理，可得
EF=HG= AC，EH=FG= BD
　又在矩形ABCD中，AC=BD
　所以，EF=FG=HG=HE
　即四边形EFGH是菱形.
（1） 顺次连结平行四边形各边中点所得的四边形是什么？
（2）顺次连结菱形各边中点所得的四边形是什么？
平行四边形
矩形
（3）顺次连结正方形各边中点所得的四边形是什么？
正方形
（4）顺次连结梯形各边中点所得的四边形是什么？
（5）顺次连结等腰梯形各边中点所得的四边形是什么？
平行四边形
菱形
（6）顺次连结对角线相等的四边形各边中点所得的四边形是什么？
（8）顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么？
（7）顺次连结对角线垂直的四边形各边中点所得的四边形是什么？
菱形
矩形
正方形
结 论
原四边形两条对角线 连接四边中点所得四边形
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
实际上，顺次连接四边形各边中点所得到的四边形一定是平行四边形，但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等，与是否互相平分无关.
它的对角线是否垂直
或者是否相等
它的对角线是否垂直
或者是否相等