人教版八年级数学下册 17.1 勾股定理 单元测试卷(含答案)
文档属性
| 名称 | 人教版八年级数学下册 17.1 勾股定理 单元测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 423.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 00:00:00 | ||
图片预览


文档简介
第十七章 勾股定理单元测试卷
一、单选题(40分)
1.下面几组数能作为直角三角形三边长的是 ( )
A.2,4,5 B.5,12,13 C.3,6,7 D.4,5,8
2.若直角三角形的三边长为5,12,m,则的值为 ( )
A.13 B.119 C.169 D.119或169
3.如图,长方形的顶点A,B在数轴上,点A表示-1,,.若以点A为圆心,对角线长为半径作弧,交数轴正半轴于点M,则点M所表示的数为( )
A. B. C. D.
4.由下列条件不能判断△ABC是直角三角形的是( )
A.∠A∶∠B∶∠C =3∶4∶5 B.∠A∶∠B∶∠C =2∶3∶5
C.∠A-∠C =∠B D.
5.等腰三角形的腰长为5,底边上的中线长为4,它的面积为 ( )
A.24 B.20 C.15 D.12
6.如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是( )
A. B. C. D.
7.如图,,且,,,则线段的长为( )
A.1.5 B.2 C.2.5 D.3
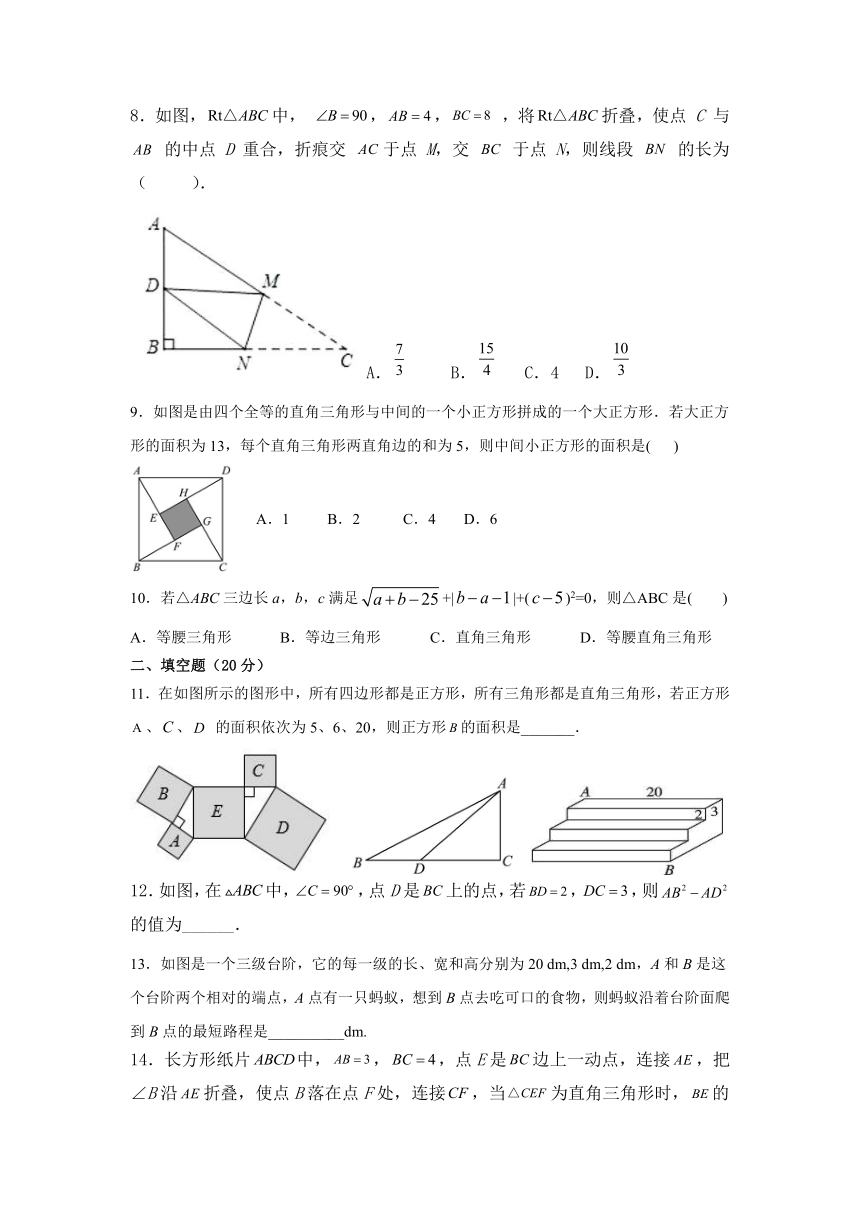
8.如图,中, ,, ,将折叠,使点 C 与 的中点 D 重合,折痕交 于点 M,交 于点 N,则线段 的长为 ( ).
A. B. C.4 D.
9.如图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.若大正方形的面积为13,每个直角三角形两直角边的和为5,则中间小正方形的面积是( )
A.1 B.2 C.4 D.6
10.若△ABC三边长a,b,c满足+||+()2=0,则△ABC是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
二、填空题(20分)
11.在如图所示的图形中,所有四边形都是正方形,所有三角形都是直角三角形,若正方形、、 的面积依次为5、6、20,则正方形的面积是_______.
12.如图,在中,,点D是上的点,若,,则的值为______.
13.如图是一个三级台阶,它的每一级的长、宽和高分别为20 dm,3 dm,2 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是__________dm.
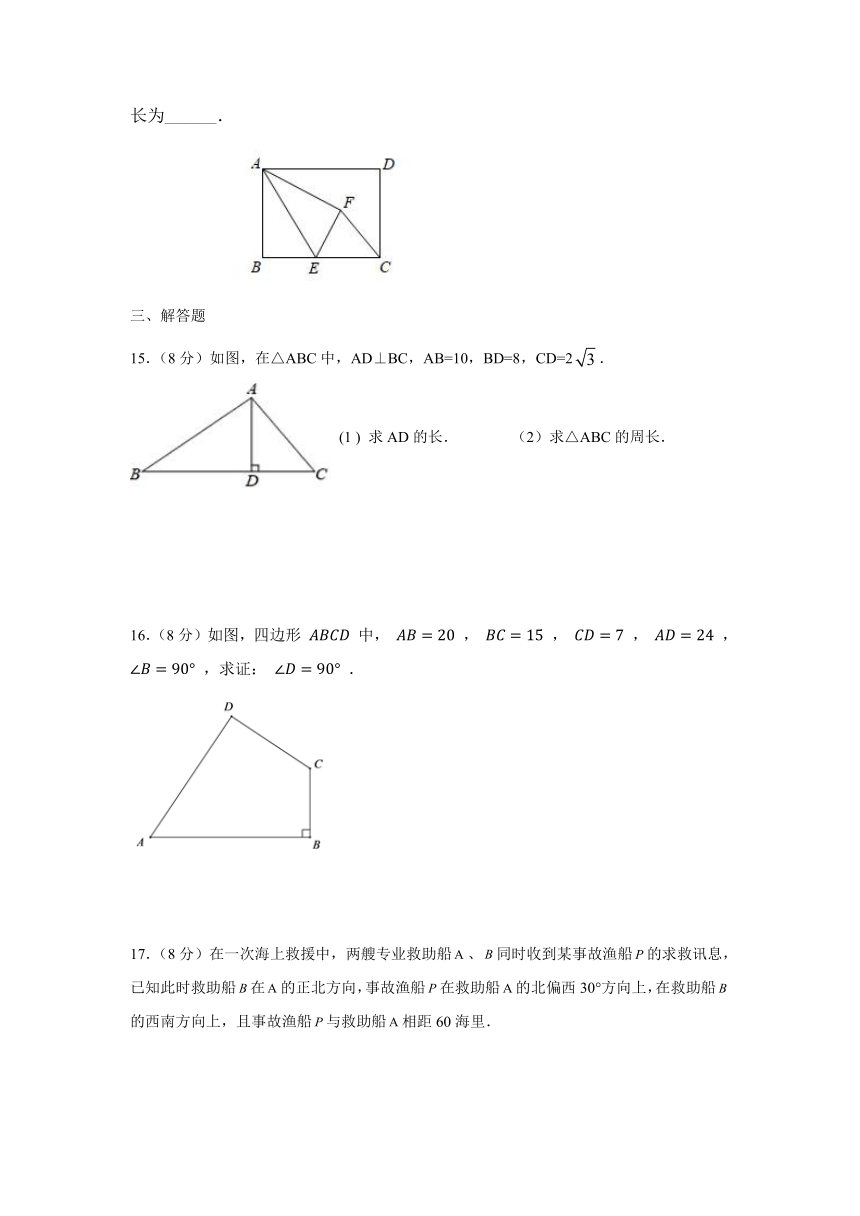
14.长方形纸片中,,,点E是边上一动点,连接,把∠B沿折叠,使点B落在点F处,连接,当为直角三角形时,的长为______.
解答题
15.(8分)如图,在△ABC中,AD⊥BC,AB=10,BD=8,CD=2.
(1 ) 求AD的长. (2)求△ABC的周长.
16.(8分)如图,四边形 中, , , , , ,求证: .
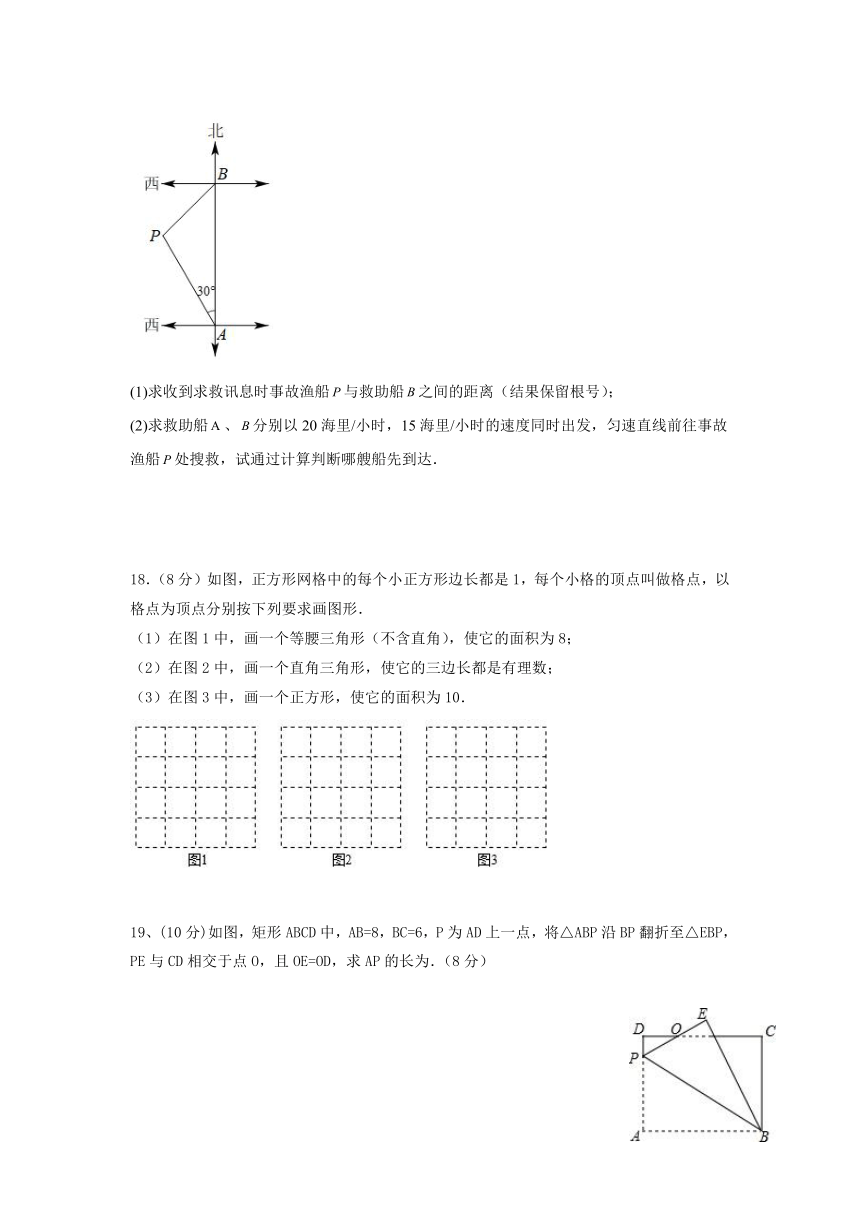
17.(8分)在一次海上救援中,两艘专业救助船、同时收到某事故渔船的求救讯息,已知此时救助船在的正北方向,事故渔船在救助船的北偏西30°方向上,在救助船的西南方向上,且事故渔船与救助船相距60海里.
(1)求收到求救讯息时事故渔船与救助船之间的距离(结果保留根号);
(2)求救助船、分别以20海里/小时,15海里/小时的速度同时出发,匀速直线前往事故渔船处搜救,试通过计算判断哪艘船先到达.
18.(8分)如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图形.
(1)在图1中,画一个等腰三角形(不含直角),使它的面积为8;
(2)在图2中,画一个直角三角形,使它的三边长都是有理数;
(3)在图3中,画一个正方形,使它的面积为10.
19、(10分)如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,求AP的长为.(8分)
20.(10分)如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16,
(1)若E是边AB的中点,求线段DE的长
(2)若E是边AB上的动点,求线段DE的最小值.
21.(12分)台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力。如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点 C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又 AB=500km,以台风中心为圆心周围250km以内为受影响区域。
(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
22.(12分)如图,在一条绷紧的绳索一端系着一艘小船.河岸上一男子拽着绳子另一端向右走,绳端从C移动到E,同时小船从A移动到B,绳子始终绷紧且绳长保持不变.(1)若CF=7米,AF=24米,AB=18米,求男子需向右移动的距离.(结果保留根号)
(2)此人以0.5米每秒的速度收绳,请通过计算回答,该男子能否在30秒内将船从A处移动到岸边点F的位置?
23.(14分)如图,在中,,,,P、Q是的边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒,点Q从点B开始沿B→C→A方向运动,且速度为每秒,它们同时出发,设出发的时间为t s.
(1) ;
(2)当t为何值时,点P在边的垂直平分线上?
(3)当点Q在边上运动时,求出使成为等腰三角形的t值.
答案
选择题
1 2 3 4 5 6 7 8 9 10
B D A A D C B B A C
11. 9
12. 16
13. 25
14. 或3;
15.解:(1)∵在△ABC中,AD是BC边上高,
∴△ADC和△ABD都是直角三角形,
在Rt△ABD中,AB =10,BD=8,
;
(2)在Rt△ACD中,
,
∴△ABC的周长=AB+AC+BD+CD
=
=.
16.解:如图,连接 ,
, , ,
, , ,
是直角三角形, 是斜边
17.(1)解:如图,过点P作于,
∴,
由题意得:海里,,,
∴海里,是等腰直角三角形,
∴海里,海里,
答:收到求救讯息时事故渔船与救助船之间的距离为海里;
(2)解:∵海里,海里,救助船分别以20海里/小时、15海里/小时的速度同时出发,
∴救助船所用的时间为(小时),
救助船所用的时间为(小时),
∵,
∴救助船先到达.
18.(1)如图所示,三角形底为4,高为4,面积为8,符合题意,即为所求;
(2)如图所示,三角形为所求,直角边分别为3,4,根据勾股定理,斜边为5,符合题意;
(3)如图所示,正方形为所求,正方形变长为,
面积为:,符合题意.
19.
20.(1)解:∵AC=21,AD=16,
∴CD=21-16=5,
∵DC +BD =5 +12 =169,BC =13 =169,
∴DC +BD =BC ,
∴△BCD是直角三角形,且∠BDC=90°,
∴∠ADB=90°,
在Rt△ADB中,由勾股定理得AB= =20,
∵∠ADB=90°,E为斜边AB的中点,
∴DE= AB= ×20=10.
(2)解:当DE⊥AB时,DE有最小值.
此时AB×DE=AD×DB,即20DE=16×12,
解得DE= .
21.(1)海港C受台风影响。
理由:如图,过点C作CD⊥AB于D,
∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2.
∴△ABC是直角三角形。
∴AC×BC=CD×AB
∴300×400=500×CD
∴CD==240(km)
∵以台风中心为圆心周围250km以内为受影响区域,
∴海港C受到台风影响。
(2)当EC=250km,FC=250km时,正好影响C港口,
∵ED==70(km),
∴EF=140km
∵台风的速度为20km/h,
∴140÷20=7(小时)
即台风影响该海港持续的时间为7小时。
22.解:(1)∵∠AFC=90°,AF=24米,CF=7米,
∴(米),
∵BF=AF﹣AB=24﹣18=6(米),
∴(米),
∴CE=AC﹣BC=(25﹣)米,
答:此人需向右移动的距离为()米.
(2)∵需收绳绳长AC﹣CF=25﹣7=18(米),
且此人以0.5米每秒的速度收绳,
∴收绳时间,
答:该男子不能在30秒内将船从A处移动到岸边点F的位置.
23.(1)12
(2)解:∵点P在边的垂直平分线上,
∴,,
在中,,即,
解得:.
(3)解:①当时,如图1所示,则,
∵,∴,,
∴,∴,
∴,∴,∴.
②当时,如图2所示,则,.
③当时,如图3所示,过点B作于点E,
∵
∴,
∴,
∴;,∴,
综上所述,当t为或或时,为等腰三角形.
一、单选题(40分)
1.下面几组数能作为直角三角形三边长的是 ( )
A.2,4,5 B.5,12,13 C.3,6,7 D.4,5,8
2.若直角三角形的三边长为5,12,m,则的值为 ( )
A.13 B.119 C.169 D.119或169
3.如图,长方形的顶点A,B在数轴上,点A表示-1,,.若以点A为圆心,对角线长为半径作弧,交数轴正半轴于点M,则点M所表示的数为( )
A. B. C. D.
4.由下列条件不能判断△ABC是直角三角形的是( )
A.∠A∶∠B∶∠C =3∶4∶5 B.∠A∶∠B∶∠C =2∶3∶5
C.∠A-∠C =∠B D.
5.等腰三角形的腰长为5,底边上的中线长为4,它的面积为 ( )
A.24 B.20 C.15 D.12
6.如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是( )
A. B. C. D.
7.如图,,且,,,则线段的长为( )
A.1.5 B.2 C.2.5 D.3
8.如图,中, ,, ,将折叠,使点 C 与 的中点 D 重合,折痕交 于点 M,交 于点 N,则线段 的长为 ( ).
A. B. C.4 D.
9.如图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.若大正方形的面积为13,每个直角三角形两直角边的和为5,则中间小正方形的面积是( )
A.1 B.2 C.4 D.6
10.若△ABC三边长a,b,c满足+||+()2=0,则△ABC是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
二、填空题(20分)
11.在如图所示的图形中,所有四边形都是正方形,所有三角形都是直角三角形,若正方形、、 的面积依次为5、6、20,则正方形的面积是_______.
12.如图,在中,,点D是上的点,若,,则的值为______.
13.如图是一个三级台阶,它的每一级的长、宽和高分别为20 dm,3 dm,2 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是__________dm.
14.长方形纸片中,,,点E是边上一动点,连接,把∠B沿折叠,使点B落在点F处,连接,当为直角三角形时,的长为______.
解答题
15.(8分)如图,在△ABC中,AD⊥BC,AB=10,BD=8,CD=2.
(1 ) 求AD的长. (2)求△ABC的周长.
16.(8分)如图,四边形 中, , , , , ,求证: .
17.(8分)在一次海上救援中,两艘专业救助船、同时收到某事故渔船的求救讯息,已知此时救助船在的正北方向,事故渔船在救助船的北偏西30°方向上,在救助船的西南方向上,且事故渔船与救助船相距60海里.
(1)求收到求救讯息时事故渔船与救助船之间的距离(结果保留根号);
(2)求救助船、分别以20海里/小时,15海里/小时的速度同时出发,匀速直线前往事故渔船处搜救,试通过计算判断哪艘船先到达.
18.(8分)如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图形.
(1)在图1中,画一个等腰三角形(不含直角),使它的面积为8;
(2)在图2中,画一个直角三角形,使它的三边长都是有理数;
(3)在图3中,画一个正方形,使它的面积为10.
19、(10分)如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,求AP的长为.(8分)
20.(10分)如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16,
(1)若E是边AB的中点,求线段DE的长
(2)若E是边AB上的动点,求线段DE的最小值.
21.(12分)台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力。如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点 C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又 AB=500km,以台风中心为圆心周围250km以内为受影响区域。
(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
22.(12分)如图,在一条绷紧的绳索一端系着一艘小船.河岸上一男子拽着绳子另一端向右走,绳端从C移动到E,同时小船从A移动到B,绳子始终绷紧且绳长保持不变.(1)若CF=7米,AF=24米,AB=18米,求男子需向右移动的距离.(结果保留根号)
(2)此人以0.5米每秒的速度收绳,请通过计算回答,该男子能否在30秒内将船从A处移动到岸边点F的位置?
23.(14分)如图,在中,,,,P、Q是的边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒,点Q从点B开始沿B→C→A方向运动,且速度为每秒,它们同时出发,设出发的时间为t s.
(1) ;
(2)当t为何值时,点P在边的垂直平分线上?
(3)当点Q在边上运动时,求出使成为等腰三角形的t值.
答案
选择题
1 2 3 4 5 6 7 8 9 10
B D A A D C B B A C
11. 9
12. 16
13. 25
14. 或3;
15.解:(1)∵在△ABC中,AD是BC边上高,
∴△ADC和△ABD都是直角三角形,
在Rt△ABD中,AB =10,BD=8,
;
(2)在Rt△ACD中,
,
∴△ABC的周长=AB+AC+BD+CD
=
=.
16.解:如图,连接 ,
, , ,
, , ,
是直角三角形, 是斜边
17.(1)解:如图,过点P作于,
∴,
由题意得:海里,,,
∴海里,是等腰直角三角形,
∴海里,海里,
答:收到求救讯息时事故渔船与救助船之间的距离为海里;
(2)解:∵海里,海里,救助船分别以20海里/小时、15海里/小时的速度同时出发,
∴救助船所用的时间为(小时),
救助船所用的时间为(小时),
∵,
∴救助船先到达.
18.(1)如图所示,三角形底为4,高为4,面积为8,符合题意,即为所求;
(2)如图所示,三角形为所求,直角边分别为3,4,根据勾股定理,斜边为5,符合题意;
(3)如图所示,正方形为所求,正方形变长为,
面积为:,符合题意.
19.
20.(1)解:∵AC=21,AD=16,
∴CD=21-16=5,
∵DC +BD =5 +12 =169,BC =13 =169,
∴DC +BD =BC ,
∴△BCD是直角三角形,且∠BDC=90°,
∴∠ADB=90°,
在Rt△ADB中,由勾股定理得AB= =20,
∵∠ADB=90°,E为斜边AB的中点,
∴DE= AB= ×20=10.
(2)解:当DE⊥AB时,DE有最小值.
此时AB×DE=AD×DB,即20DE=16×12,
解得DE= .
21.(1)海港C受台风影响。
理由:如图,过点C作CD⊥AB于D,
∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2.
∴△ABC是直角三角形。
∴AC×BC=CD×AB
∴300×400=500×CD
∴CD==240(km)
∵以台风中心为圆心周围250km以内为受影响区域,
∴海港C受到台风影响。
(2)当EC=250km,FC=250km时,正好影响C港口,
∵ED==70(km),
∴EF=140km
∵台风的速度为20km/h,
∴140÷20=7(小时)
即台风影响该海港持续的时间为7小时。
22.解:(1)∵∠AFC=90°,AF=24米,CF=7米,
∴(米),
∵BF=AF﹣AB=24﹣18=6(米),
∴(米),
∴CE=AC﹣BC=(25﹣)米,
答:此人需向右移动的距离为()米.
(2)∵需收绳绳长AC﹣CF=25﹣7=18(米),
且此人以0.5米每秒的速度收绳,
∴收绳时间,
答:该男子不能在30秒内将船从A处移动到岸边点F的位置.
23.(1)12
(2)解:∵点P在边的垂直平分线上,
∴,,
在中,,即,
解得:.
(3)解:①当时,如图1所示,则,
∵,∴,,
∴,∴,
∴,∴,∴.
②当时,如图2所示,则,.
③当时,如图3所示,过点B作于点E,
∵
∴,
∴,
∴;,∴,
综上所述,当t为或或时,为等腰三角形.
