5.2圆的对称性(1)[下学期]
图片预览

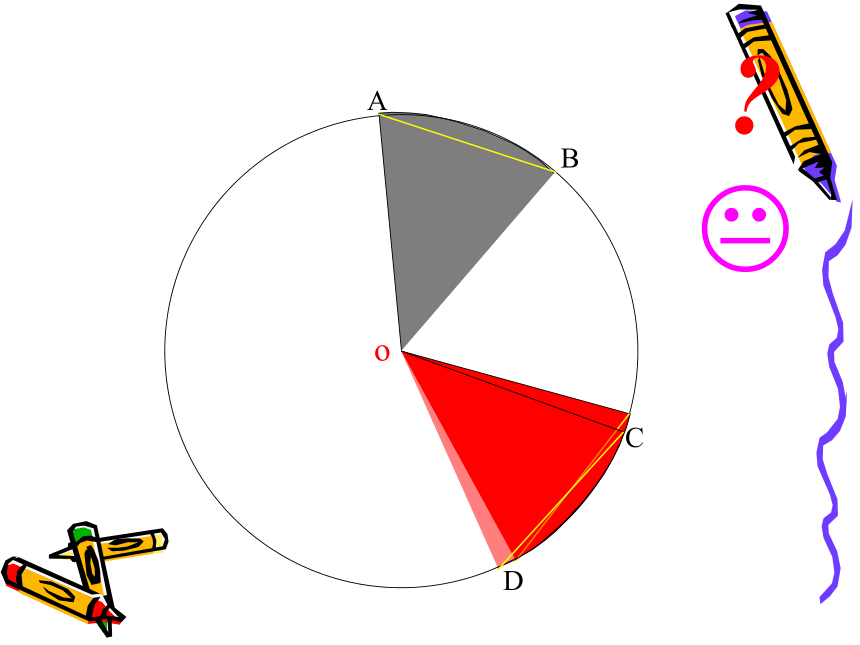
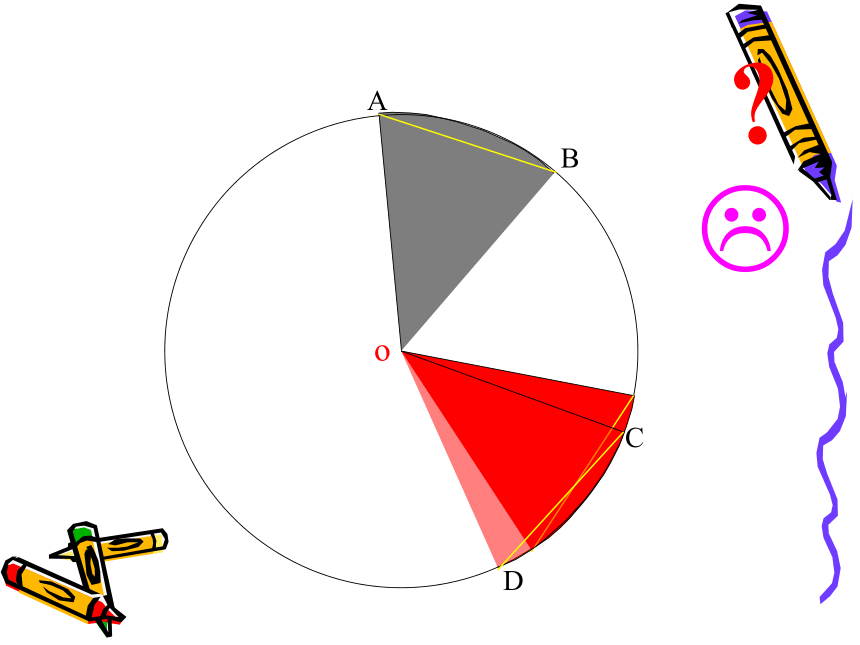
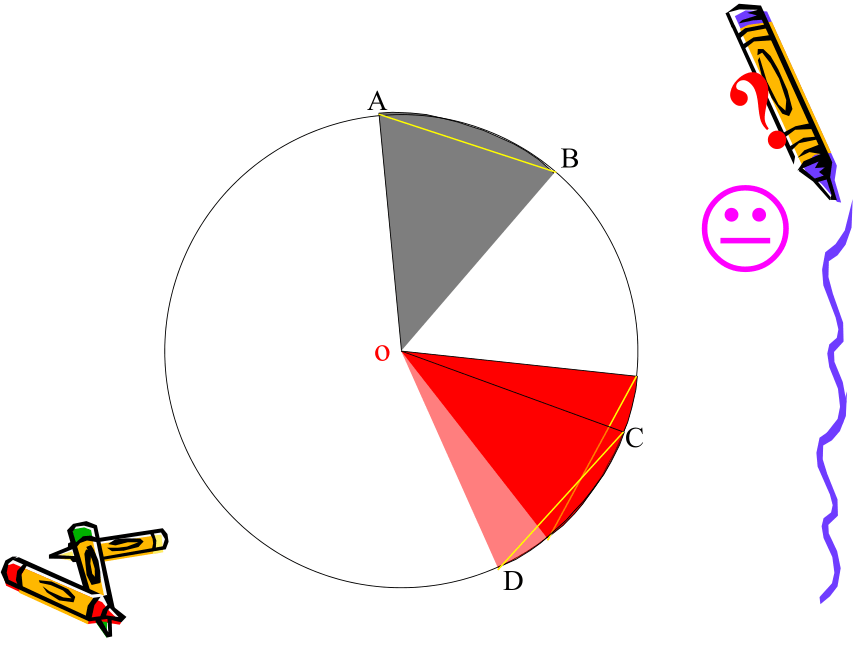
文档简介
课件35张PPT。
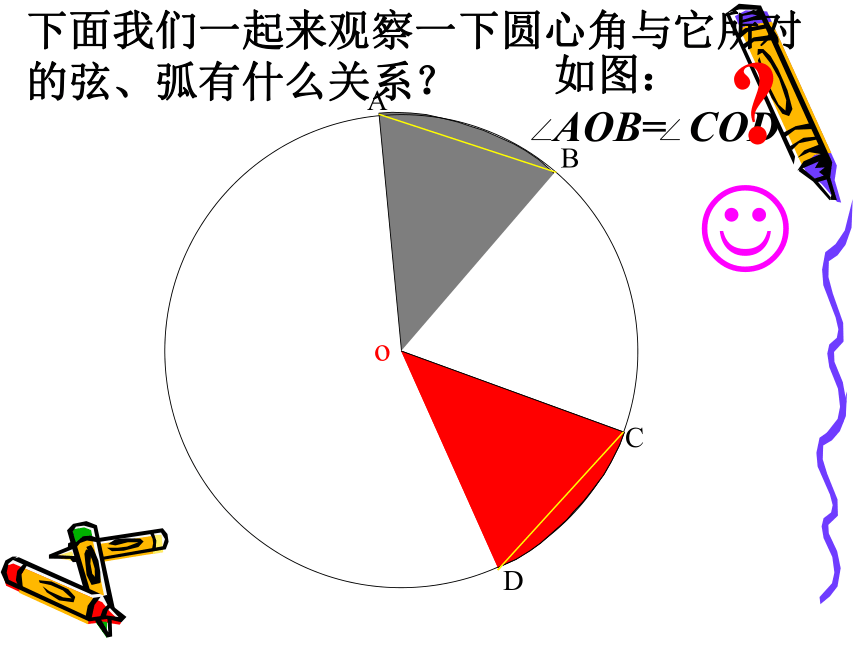
圆的对称性ABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系???ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo???? ∵∠AOB= ∠COD,
∴半径OB与OA重合,
∴ 点A与点C重合,点B与点D重合。
∴ AB=CD,
根据圆的性质,AB与CD重合。
此时,称作 两条圆弧相等。
记作:“AB=CD” ⌒⌒⌒⌒上面的结论,在两个等圆中也成立。于是有下面定理:圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相 等,所对的弦也相等。
例 如图,AC与BD为⊙O的两条互 相垂直的直径.
求证:AB=BC=CD=DA;
AB=BC=CD=DA.⌒⌒⌒⌒∵把圆心角等分成功360份,则每一份的圆心角是1o.同时整个圆也被分成了360份.则每一份这样的弧叫做1o的弧.这样,1o的圆心角对着1o的弧,
1o的弧对着1o的圆心角.
n o的圆心角对着no的弧,
n o的弧对着no的圆心角.性质:弧的度数和它所对圆心角的度数相等.小结圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.由条件:
①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′补充定理拓展与深化在同圆或等圆中,如果轮换下面五组条件:
①两个圆心角,②两条弧,③两条弦,④两条弦心距,你能得出什么结论?与同伴交流你的想法和理由.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′练习:
1.在半径相等的⊙O和⊙O 中,A’B’和A B 所对的圆心角都是60°.
(1)AB和A’ B’各是多少度?
(2)AB和A’ B’ 相等吗?
(3)在同圆或等圆中,度数相等的弧相等.为什么?
2.若把圆5等分,那么每一份弧是多少度?若把圆8等分,那么每一份弧是多少度?
3.圆心到弦的距离叫做这条弦的弦心距.求证:在同圆或等圆中,相等的圆心角所对的弦的弦心距相等.⌒⌒⌒⌒⌒⌒ 谢 谢
圆的对称性ABCDo下面我们一起来观察一下圆心角与它所对的弦、弧有什么关系???ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo??ABCDo???? ∵∠AOB= ∠COD,
∴半径OB与OA重合,
∴ 点A与点C重合,点B与点D重合。
∴ AB=CD,
根据圆的性质,AB与CD重合。
此时,称作 两条圆弧相等。
记作:“AB=CD” ⌒⌒⌒⌒上面的结论,在两个等圆中也成立。于是有下面定理:圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相 等,所对的弦也相等。
例 如图,AC与BD为⊙O的两条互 相垂直的直径.
求证:AB=BC=CD=DA;
AB=BC=CD=DA.⌒⌒⌒⌒∵把圆心角等分成功360份,则每一份的圆心角是1o.同时整个圆也被分成了360份.则每一份这样的弧叫做1o的弧.这样,1o的圆心角对着1o的弧,
1o的弧对着1o的圆心角.
n o的圆心角对着no的弧,
n o的弧对着no的圆心角.性质:弧的度数和它所对圆心角的度数相等.小结圆心角, 弧,弦,弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等,所对的弦的弦心距相等.由条件:
①∠AOB=∠A′O′B′③AB=A′B′④ OD=O′D′补充定理拓展与深化在同圆或等圆中,如果轮换下面五组条件:
①两个圆心角,②两条弧,③两条弦,④两条弦心距,你能得出什么结论?与同伴交流你的想法和理由.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′练习:
1.在半径相等的⊙O和⊙O 中,A’B’和A B 所对的圆心角都是60°.
(1)AB和A’ B’各是多少度?
(2)AB和A’ B’ 相等吗?
(3)在同圆或等圆中,度数相等的弧相等.为什么?
2.若把圆5等分,那么每一份弧是多少度?若把圆8等分,那么每一份弧是多少度?
3.圆心到弦的距离叫做这条弦的弦心距.求证:在同圆或等圆中,相等的圆心角所对的弦的弦心距相等.⌒⌒⌒⌒⌒⌒ 谢 谢
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
