圆周角[上学期]

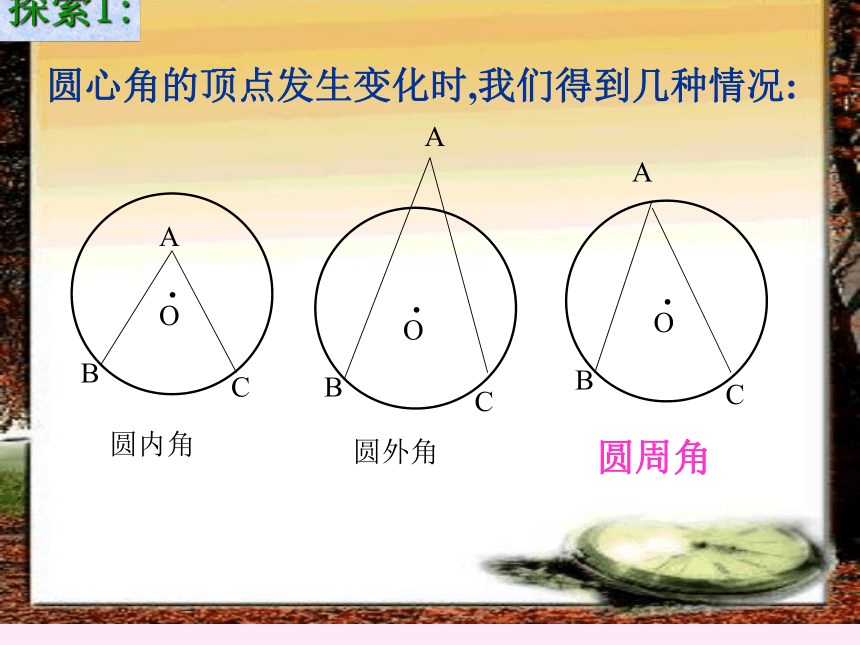
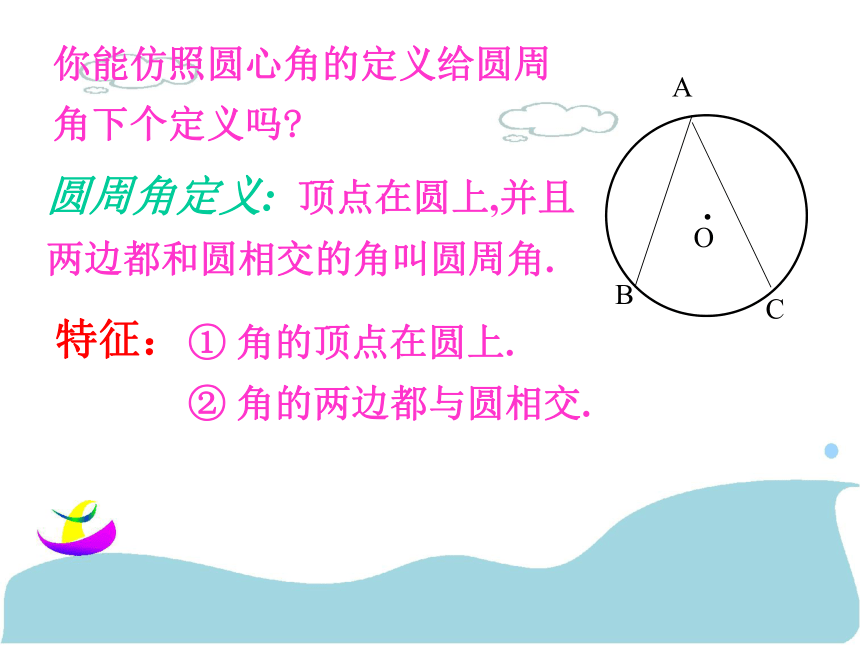
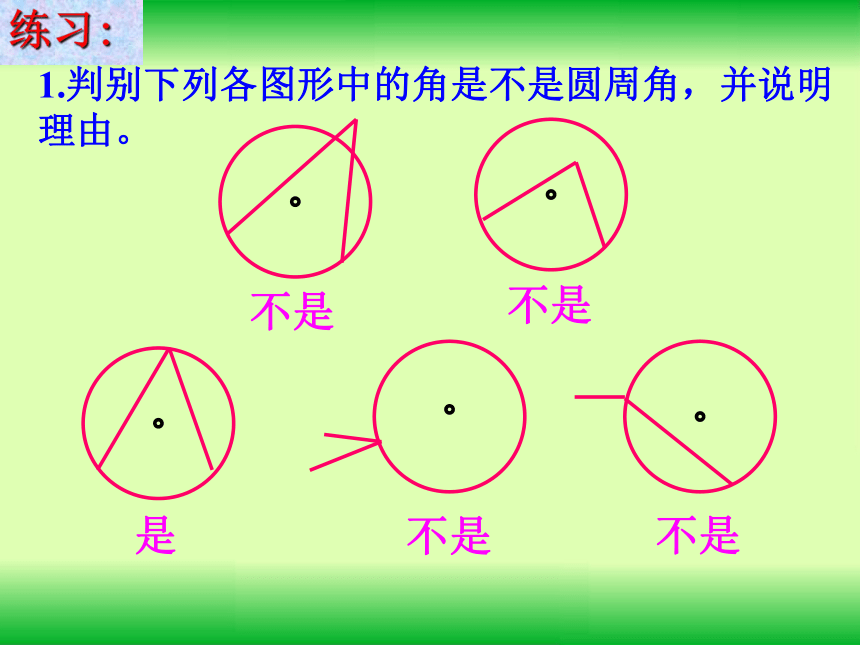
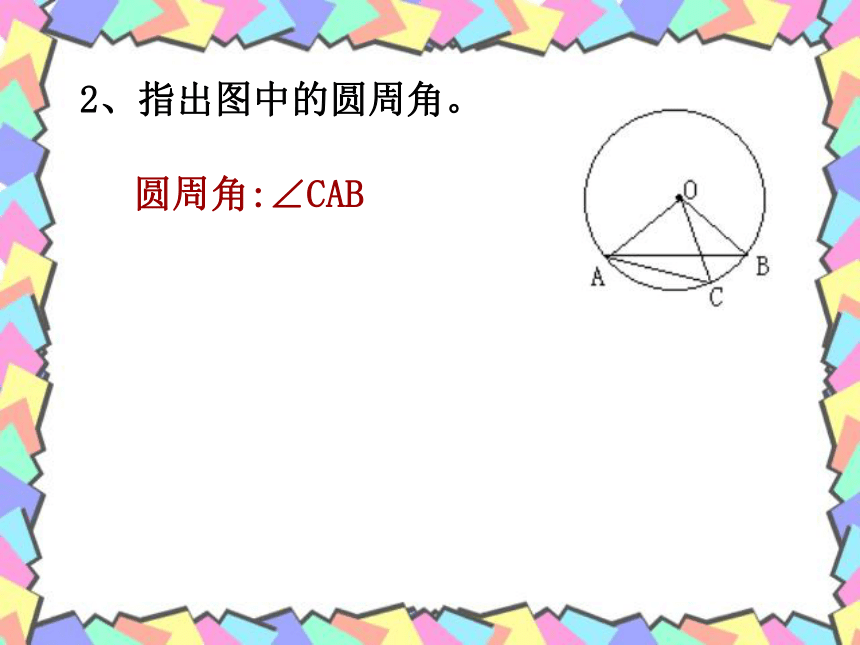
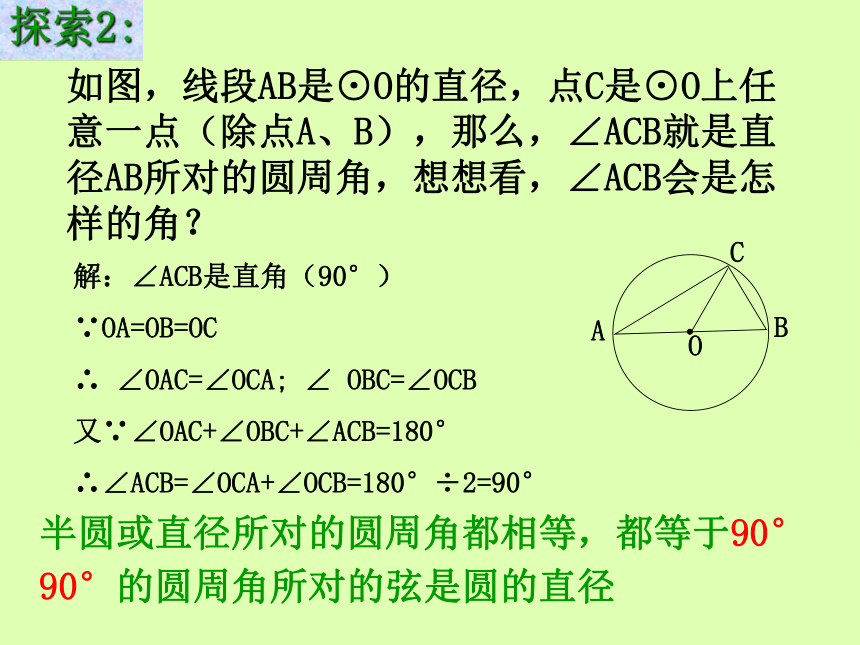
课件18张PPT。23.1圆周角欢迎各位老师指导百官中学数学组一. 复习引入:1.圆心角的定义?在同圆（或等圆）中，如果圆心角、弧、弦有一组量相等，那么它们所对应的其余两个量都分别相等。答:顶点在圆心的角叫圆心角2.上节课我们学习了一个反映圆心角、弧、弦三个量之间关系的一个结论，这个结论是什么？圆心角的顶点发生变化时,我们得到几种情况:A.OBCAA圆内角圆外角圆周角探索1:你能仿照圆心角的定义给圆周角下个定义吗?圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.特征：1.判别下列各图形中的角是不是圆周角，并说明理由。不是不是是不是不是练习:2、指出图中的圆周角。圆周角:∠CAB探索2:如图，线段AB是⊙O的直径，点C是⊙O上任意一点（除点A、B），那么，∠ACB就是直径AB所对的圆周角，想想看，∠ACB会是怎样的角？解：∠ACB是直角（90°）
∵OA=OB=OC
∴ ∠OAC=∠OCA; ∠ OBC=∠OCB
又∵∠OAC+∠OBC+∠ACB=180°
∴∠ACB=∠OCA+∠OCB=180°÷2=90°半圆或直径所对的圆周角都相等，都等于90°90°的圆周角所对的弦是圆的直径画一个圆心角,然后再画同弧所对的圆周角.1.同一条弧你能画多少个圆周角?多少个圆
心角?用量角器量一量这些
圆周角你有何发现？2.再用量角器量出圆心角的度数,你有何发现 呢?发现:一条弧所对的圆周角等于它所对的圆心角的一半.探索2:发现:在同圆(或等圆)中,同弧或等弧所
对的圆周角相等3.虽然一条弧所对的圆周角有无数个,但它们与圆心的位置有几种情况?发现:一条弧所对的圆周角等于它所对的圆
心角的一半.分三种情况来证明：
（1）圆心在∠BAC的一边上.
（2）圆心在∠BAC的内部.（3）圆心在∠BAC的外部.D结论 在同圆(或等圆)中，同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半；相等的圆周角所对的弧相等。练习:130°4、在⊙O中，一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°，则x=_ _；3. 如图，在直径为AB的半圆中，O为圆心，C、D
为半圆上的两点，∠COD=50°，则
∠CAD=______；20°50°1.AB、AC为⊙O的两条弦，延长CA到D，使 AD=AB，如果∠ADB=35° ，
求∠BOC的度数。∠BOC =140° ∠A=21° 1.圆周角定义:顶点在圆上,并且两边都和圆相交的角叫圆周角.3.在同圆(或等圆)中，同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半；相等的圆周角所对的弧相等。2.半圆或直径所对的圆周角都相等，都等于90°
90°的圆周角所对的弦是圆的直径小结:作业: