5.4 确定圆的条件[上学期]

课件18张PPT。确定圆的条件探究（1）
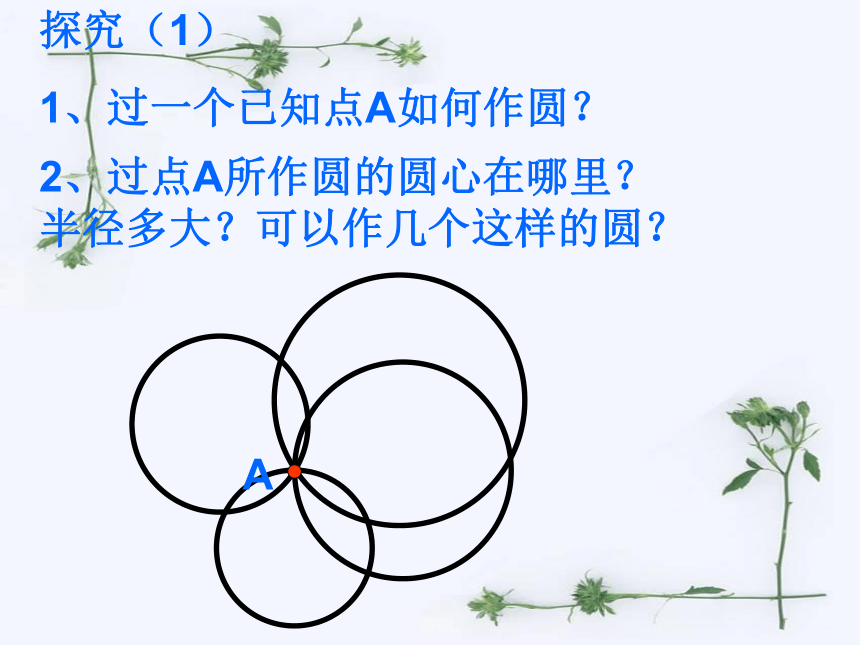
1、过一个已知点A如何作圆？A2、过点A所作圆的圆心在哪里？
半径多大？可以作几个这样的圆？探究（2）
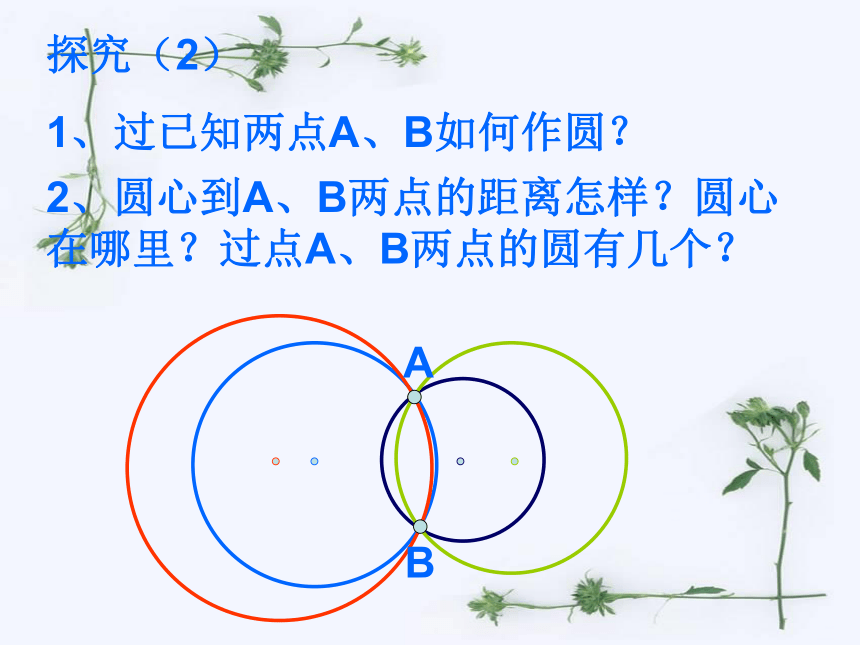
1、过已知两点A、B如何作圆？2、圆心到A、B两点的距离怎样？圆心在哪里？过点A、B两点的圆有几个？ 探究（3）
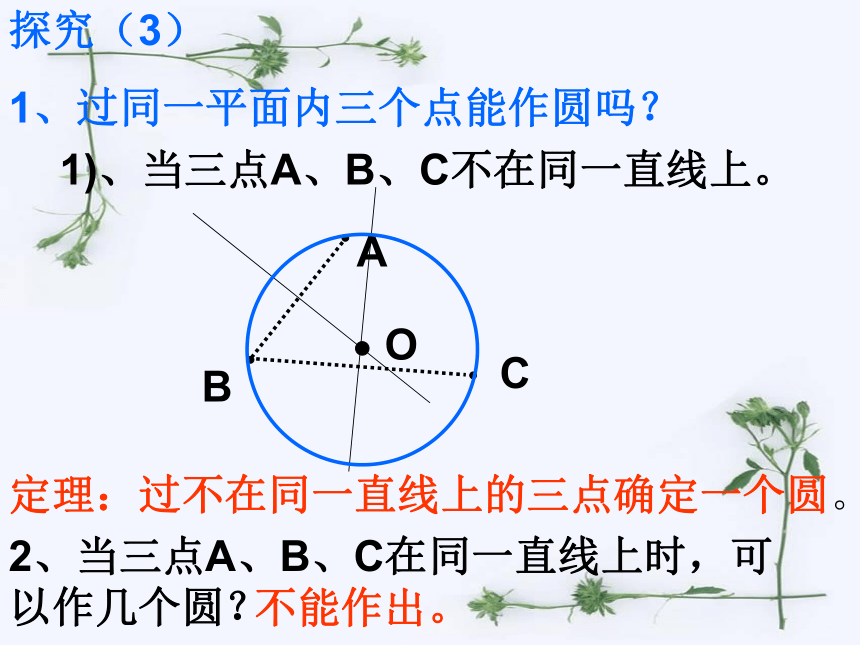
1、过同一平面内三个点能作圆吗？1)、当三点A、B、C不在同一直线上。定理：过不在同一直线上的三点确定一个圆。2、当三点A、B、C在同一直线上时，可以作几个圆？
不能作出。探究（4）
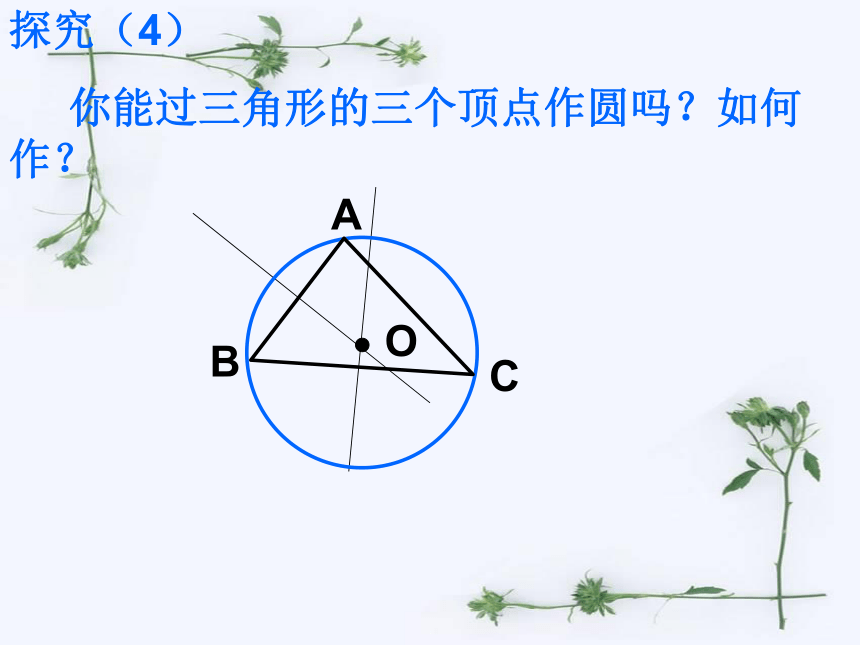
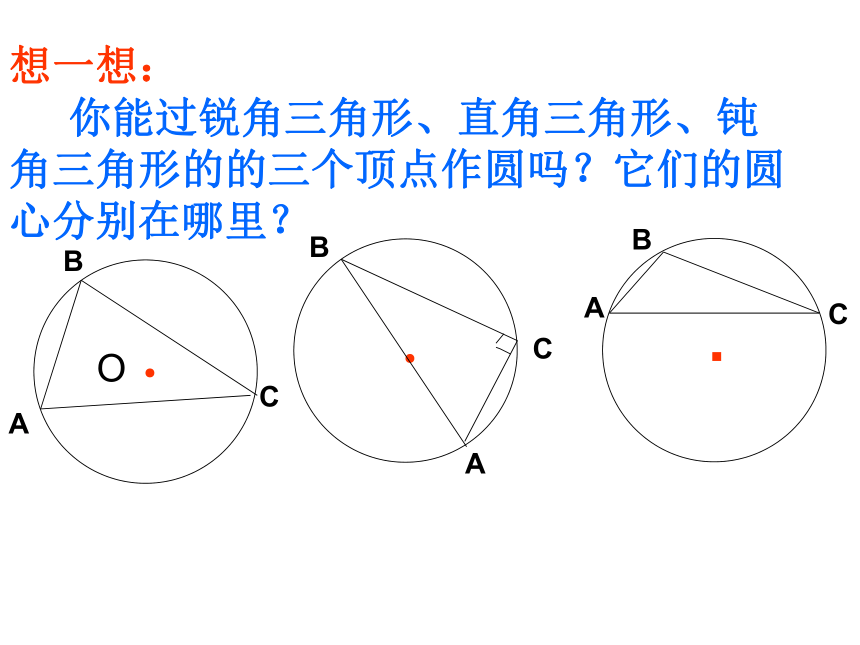
你能过三角形的三个顶点作圆吗？如何作？ABC想一想：
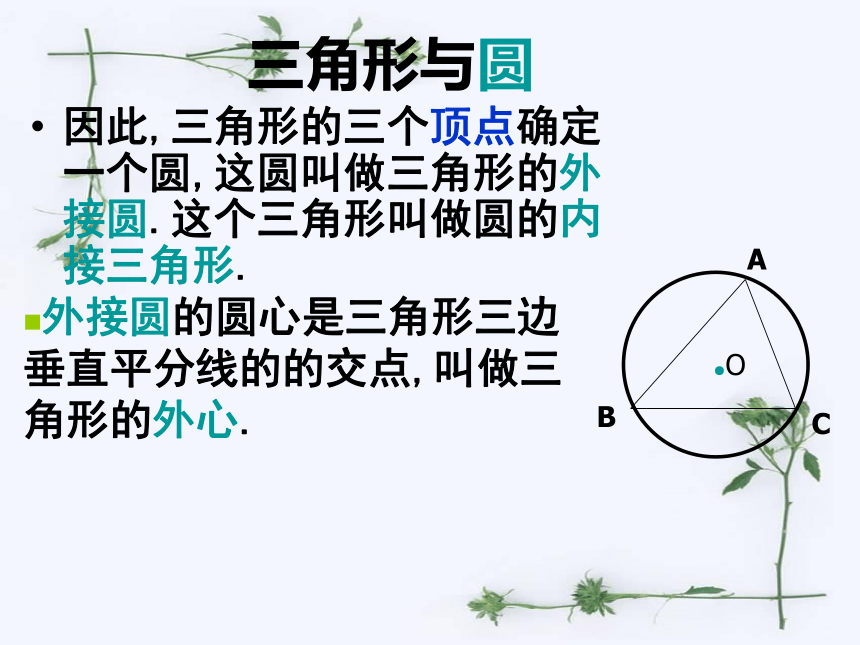
你能过锐角三角形、直角三角形、钝角三角形的的三个顶点作圆吗？它们的圆心分别在哪里？三角形与圆因此,三角形的三个顶点确定一个圆,这圆叫做三角形的外接圆.这个三角形叫做圆的内接三角形.外接圆的圆心是三角形三边垂直平分线的的交点,叫做三角形的外心. 1.锐角三角形的外心在三角形的内部。
2.直角三角形的外心在三角形的斜边上，
且是斜边的中点
3.钝角三角形的外心在三角形的外部
老师提示:
多边形的顶点与圆的位置关系称为接.如果四边形的四个顶点在一个圆,这圆叫做四边形的外接圆.这个四边形叫做圆的内接四边形.我们可以证明圆内接四边的两个重要性质:
1.圆内接四边形对角互补.
2.圆内接四边形对的一个外角等于它的内对角.
3.对角互补的四边形内接于圆.四边形与圆CODBA如图：圆内接四边形ABCD中， ∵ ∠BAD等于弧BCD所对圆心角的一半,∠BCD等于弧BAD所对圆心角的一半.
而弧BCD所对的圆心角+弧BAD所对的圆心角=360°， ∴∠BAD＋∠BCD＝180°. 同理∠ABC＋∠ADC＝180°.圆内接四边形的对角互补.四边形与圆如果延长BC到E，那么
∠DCE＋∠BCD ＝180°.∴∠A＝∠DCE.又 ∵∠A ＋∠BCD＝180°，因为∠A是与∠DCE相邻的内角∠DCB的对角,我们把∠A叫做∠DCE的内对角.圆内接四边形的一个外角等于它的内对角.四边形与圆完成填空：
如图：⊙O是△ ABC的 圆， △ ABC 是⊙O的 　 三角形，O是△ ABC的 心，它是 的交点，到三角形 的距离相等。 ●练习例1、判断：
1、经过三点一定可以作圆。（ ）
2、三角形的外心就是这个三角形两边垂直平分线的交点。（ ）
3、三角形的外心到三边的距离相等。（ ）
4、经过不在一直线上的四点能作一个圆。（ ）练习例2、填空：
1、已知⊙O的半径为4，OP＝3.4，则P在⊙O的 （ ）。
2、已知 点P在 ⊙O的外部，OP＝5，那么⊙O的半径r满足（ ）
3、 已知⊙O的半径为5，M为ON的中点，当OM＝3时，N点与⊙O的位置关系是N在⊙O的（ ）思考1、过三角形的三个顶点是否都可以作圆？为什么？
2、一个三角形的外接圆有几个？一个圆的内接三角形有几个？为什么？
3、三角形的外心有什么性质？它一定在三角形的内部吗？画图说明。应用 某一个城市在一块空地新建了三个居民小区，它们分别为A、B、C，且三个小区不在同一直线上，要想规划一所中学，使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置？你怎么确定这个位置呢？
●●●BAC反思自我想一想,你的收获和困惑有哪些?说出来,与同学们分享.