直线与圆的位置关系(2)[上学期]

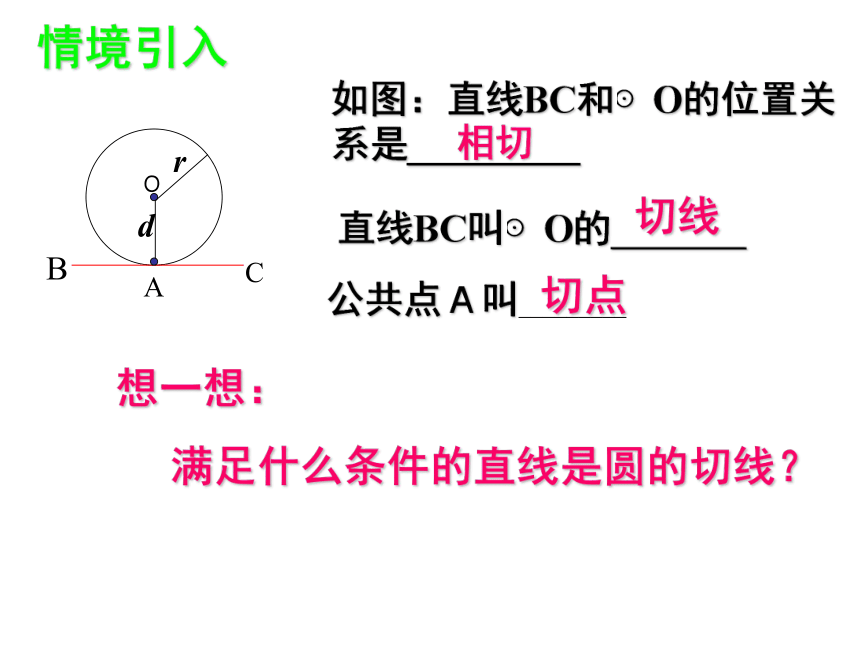
课件20张PPT。直线与圆的位置关系（2）情境引入如图：直线BC和⊙O的位置关系是_________切线切点公共点Ａ叫_________想一想：
　满足什么条件的直线是圆的切线？直线BC叫⊙O的_______相切已知⊙O和⊙O上的一点D，如何过点D画⊙O的切线？不妨在直线l 上任意取一点P（点D除外），连结OP，则OP＞OD∴点P在⊙O外∴l 与⊙O只有一个公共点D。∴l 与⊙O相切l切线识别方法：
经过半径外端并且垂直于这条半径的直线是圆的切线。判断下图中的l 是否为⊙O的切线⑴半径⑵外端⑶垂直巩固练习 1、如图，已知点B在⊙O上。根据下列条件，能否判定直线AB和⊙O相切？⑴OB=7,AO=12,AB=6⑵∠O=68.5°,∠A=21°30′？2、如图，AB是⊙O的直径， AT=AB，∠ABT=45°。
求证：AT是⊙O的切线巩固练习？思考与探索？直线l 与⊙O相切于点A，连接OA，则OA是过切点的半径，直线l 与半径OA是否一定垂直？你能说明理由吗？归纳： 切线的性质
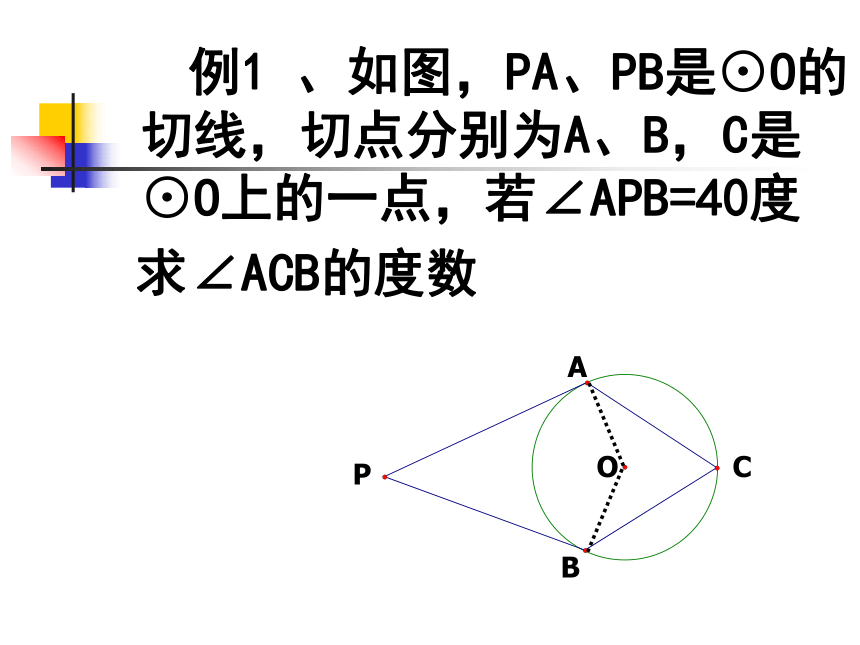
圆的切线垂直于过切点的半径 例1 、如图，PA、PB是⊙O的切线，切点分别为A、B，C是⊙O上的一点，若∠APB=40度
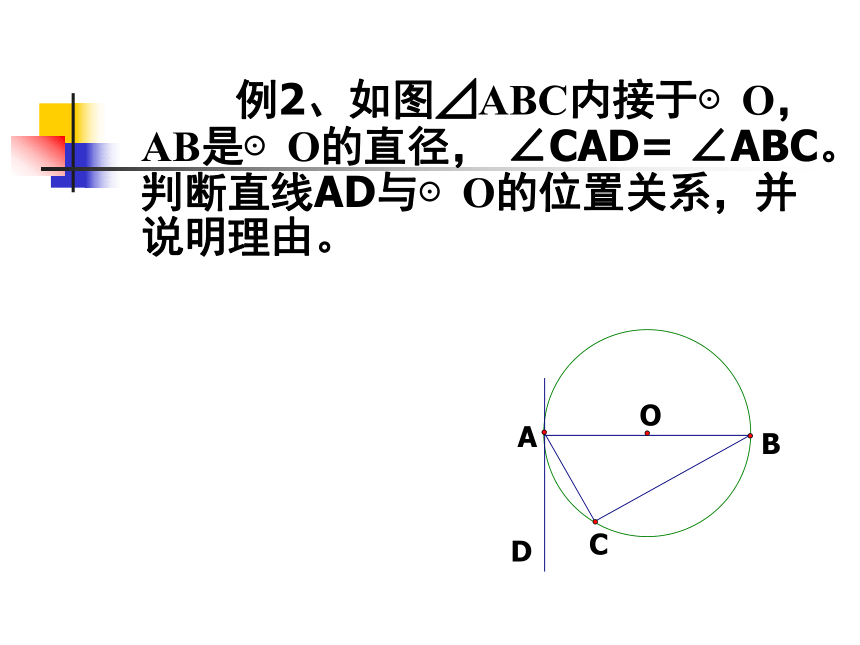
求∠ACB的度数A 例2、如图⊿ABC内接于⊙O，AB是⊙O的直径， ∠CAD= ∠ABC。判断直线AD与⊙O的位置关系，并说明理由。例3、如图已知直线AB过⊙O上的点C，并且
OA＝OB，CA＝CB 求证：直线ＡＢ是⊙O的切线证明：连接OC∵　OA=OB，CA=CB∴　OC是等腰三角形OAB底边AB上的中线∴　　AB⊥OC直线ＡＢ经过半径ＯＣ的外端C，并且垂直于半径OC，所以AB是⊙O的切线例4 ：如图A是⊙O外的一点，AO的延长线交⊙O于C，直线AB经过⊙O上一点B，且AB＝BC，∠C＝30°。
求证：直线AB是⊙O的切线证明：连结OB∵OB=OC,AB=BC,∠C=30°
∴∠OBC=∠C=∠A=30°
∴∠AOB=∠C+∠OBC=60°
∴∠ABO=180°－(∠AOB+∠A)
=180°－(60°+30°)
=90° ∴ AB是⊙O的切线例5、如图：点O为∠ABC平分线上一点， OD⊥AB于D，以O为圆心，OD为半径作圆。 　求证：BC是⊙O 的切线。证明：作OE⊥BC于E∵　点O为∠ABC平分线上一点
　　OD⊥AB于D∴　OE＝OD又∵　OD为⊙O半径圆心Ｏ到直线BC的距离等于半径，所以BC与⊙O相切2、d与r的数量关系：当圆心到直线的距离d等于圆的半径r时，该直线是这个圆的切线切线识别方法：归纳与发现1、定义：若一直线与圆只有一个公共点，这条直线是该圆的切线。3、经过半径外端并且垂直于这条半径的直线是圆的切线。作OE⊥BC于E　　当已知条件中没有明确直线与圆是否有公共点时　　辅助线：是过圆心作这条　　　　　　直线的垂线段。　　再证明这条垂线段的长等于半径。连结OC　　当已知条件中直线与圆已有一个公共点时　　辅助线：是连结圆心和这　　　　　　个公共点。再证明这条半径与直线垂直。例3、如图已知直线AB过⊙O上的点C，并且OA＝OB，CA＝CB
求证：直线ＡＢ是⊙O的切线例5、如图：点O为∠ABC平分线上一点，OD⊥AB于D，以O为圆心，OD为半径作圆。 　求证：BC与作⊙O相切。判定一条直线是圆的切线的三种方法　　１、利用定义：与圆有唯一公共点的直线　　　　　　　　　是圆的切线。２、利用数量关系：与圆心距离等与圆的半　　　　　　　 径的直线是圆的切线。３、经过半径的外端并且垂直于　　　　　　　　　这条半径的直线是圆的切线。小结２、填空：
在三角形OAB中,若OA=4,OB=4,圆O的半径是2,则当∠AOB=________时,直线AB与圆O相切。 １、选择：下列直线能判定为圆的切线是（　）
　　　　　　A、与圆有公共点的直线　　　　
　　　　　　B、垂直于圆的半径的直线
　　　　　　C、过圆的半径外端的直线　　　
　　　　　　D、到圆心的距离等于该圆半径的直线练习D120度３、证明题：
(１)、如图：AB为⊙O直径，⊙O过BC中点D，
DE ⊥ AC　垂足为E
求证：DE是⊙O的切线练习　　
(２)、如图,Rt⊿ABC中, ∠B=90度, ∠ A的平分线交BC于点D,以D为圆心,DB长为半径作⊙D
试说明:AC是⊙D的切线练习4、如图，AB是⊙O的直径，弦AD平分∠BAC，
过A作AC⊥DC，
求证：DC是⊙O的切线。巩固练习？5 如图，已知四边形ABCD是直角梯形，AD∥BC，AB⊥BC，CD＝AD＋BC。
求证：以CD为直径的⊙O与AB相切证明：过点O作OE⊥AB,垂足为E。∵AD∥BC,AB⊥BC, ∴ AD⊥AB
而OE⊥AB ∴ AD∥OE∥BC巩固练习？