北京市海淀区师达中学2022~2023学年第二学期初三数学大练习试卷(4月)(无答案)
文档属性
| 名称 | 北京市海淀区师达中学2022~2023学年第二学期初三数学大练习试卷(4月)(无答案) | 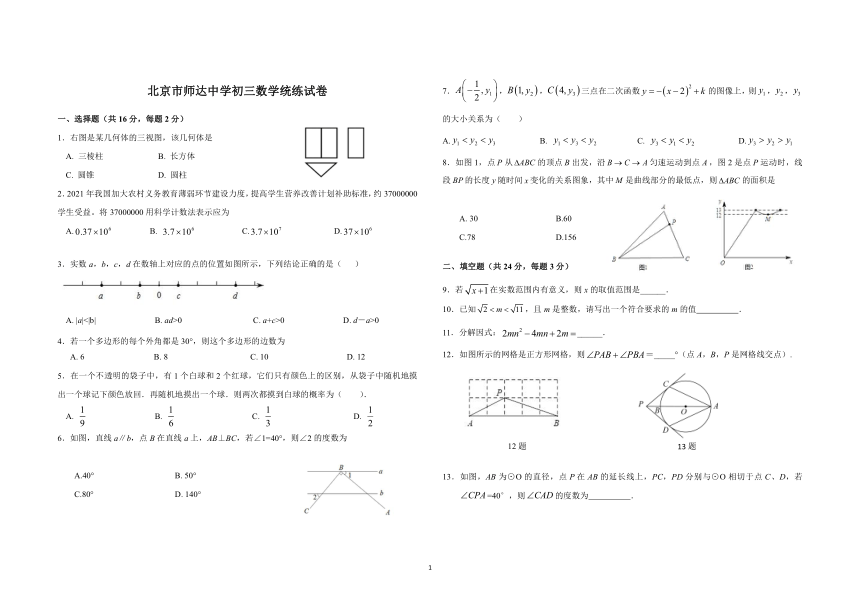 | |
| 格式 | zip | ||
| 文件大小 | 275.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 21:00:29 | ||
图片预览

文档简介
北京市师达中学初三数学统练试卷
一、选择题(共16分,每题2分)
1.右图是某几何体的三视图,该几何体是
A. 三棱柱 B. 长方体
C. 圆锥 D. 圆柱
2.2021年我国加大农村义务教育薄弱环节建设力度,提高学生营养改善计划补助标准,约37000000学生受益。将37000000用科学计数法表示应为
A. B. C. D.
3.实数a,b,c,d在数轴上对应的点的位置如图所示,下列结论正确的是( )
A. |a|<|b| B. ad>0 C. a+c>0 D. d-a>0
4.若一个多边形的每个外角都是30°,则这个多边形的边数为
A. 6 B. 8 C. 10 D. 12
5.在一个不透明的袋子中,有1个白球和2个红球,它们只有颜色上的区别,从袋子中随机地摸出一个球记下颜色放回.再随机地摸出一个球.则两次都摸到白球的概率为( ).
A. B. C. D.
6.如图,直线a∥b,点B在直线a上,AB⊥BC,若∠1=40°,则∠2的度数为
A.40° B. 50°
C.80° D. 140°
7.,,三点在二次函数的图像上,则,,的大小关系为( )
A. B. C. D.
8.如图1,点从的顶点出发,沿匀速运动到点,图2是点运动时,线段的长度随时间变化的关系图象,其中是曲线部分的最低点,则的面积是
A. 30 B.60 C.78 D.156
二、填空题(共24分,每题3分)
9.若在实数范围内有意义,则x的取值范围是______.
10.已知,且m是整数,请写出一个符合要求的m的值 .
11.分解因式:______.
12.如图所示的网格是正方形网格,则=_____°(点A,B,P是网格线交点).
13.如图,AB为⊙O的直径,点P在AB的延长线上,PC,PD分别与⊙O相切于点C、D,若=40°,则的度数为 .
14.如图,反比例函数的图象经过点(2,1).当y<1时,x的取值范围是 .
15.如图,在矩形中,是边的中点,连结交对角线于点,若,则的长为__________.
16. 某工厂生产I号、II号两种产品,并将产品按照不同重量进行包装,已知包装产品款式有三种:A款,B款,C款,且三款包装的重量及所含I号、II号产品的重量如下表:
包装款式 包装的重量(吨) 含I号新产品的重量(吨) 含II号产品的重量(吨)
A款 6 3 3
B款 5 3 2
C款 5 2 3
现用一辆最大载重量为28吨的货车一次运送5个包装产品,且每种款式至少有1个.
(1)若恰好装运28吨包装产品,则装运方案中A款、B款、C款个数依次为 ;
(2)若装运的I号产品不超过13吨.同时装运的II号产品最多,则装运方案中A款、B款、C款的个数依次为 .(写出一种即可)
三、解答题(共60分,第17-18题,每题5分,第19-24题6分,第25-26题,每题7分)
17.计算: 18.解不等式组:
19.已知关于x的方程有两个实数根.
(1)求k的取值范围;
(2)当k取最大整数时,求此时方程的根.
20.我们把连接三角形两边中点的线段叫做三角形的中位线.三角形的中位线有如下性质:三角形的中位线平行于三角形的第三边并且等于第三边的一半.下面请对这个性质进行证明.
(1)如图1,点,分别是的边,的中点,求证:,且;
(2)如图2,点是边的中点,点是边的中点,若,,,直接写出的长=______.
21.在平面直角坐标系中,函数的图象经过点.
(1)求该函数的解析式;
(2)当时,对于x的每一个值,函数的值都小于函数的值,直接写出m的取值范围
(3)若反比例函数的图象与函数的图象交于点A,B.若,直接写出b的取值范围.
22.如图所示,△ABC中,∠ACB=90°,D,E分别为AB,BC的中点,连接DE并延长到点F,使得EF=DE,连接CD,CF,BF.
(1)求证:四边形BFCD是菱形;
(2)若,DE=5,求菱形BFCD的面积.
23.小明在“生活中的数学”探究活动中,经过市场调查,研究了某种商品的售价、销量、利润之间的变化关系.小明整理出该商品的相关数据如下表所示.
时间x(天) 1≤x<30 30≤x≤60
售价(元/件) x+40 70
每天销量(件) 100-2x
已知该商品的进价为每件10元,设销售该商品的每天利润为y元.
(1)求y与x的函数关系式;
(2)求销售该商品第几天时,当天销售利润最大,最大利润是多少?
24.如图,为⊙的直径,为⊙上一点,过点
作⊙的切线,过点作于点.
(1)求证:;
(2)若,,求的长.
25.在平面直角坐标系xOy中,抛物线与x轴的交点为点A(1,0)和点B.
(1)用含的式子表示;
(2)求抛物线的对称轴和点B的坐标;
(3)分别过点P(t,0)和点Q ( t+2, 0)作x轴的垂线,交抛物线于点M和点N,记抛物线在M,N之间的部分为图象G(包括M,N两点).记图形G上任意一点的纵坐标的最大值是m,最小值为n.
当a=1时,求m-n的最小值;
若存在实数t,使得m-n =1,直接写出a的取值范围.
26.在Rt△ABC中,∠ABC=90°,∠BAC=30°,D为边BC延长线上一动点,点E在边AC延长线上,CE=CD.点D关于点B的对称点为点F,连接AD,EF.
(1)设CD=a,BC=b.判断AE与CF的数量关系,并证明
(2)取AD中点P,连接PE、PF,补全图形,判断PE与PF的数量关系与位置关系,并证明.
一、选择题(共16分,每题2分)
1.右图是某几何体的三视图,该几何体是
A. 三棱柱 B. 长方体
C. 圆锥 D. 圆柱
2.2021年我国加大农村义务教育薄弱环节建设力度,提高学生营养改善计划补助标准,约37000000学生受益。将37000000用科学计数法表示应为
A. B. C. D.
3.实数a,b,c,d在数轴上对应的点的位置如图所示,下列结论正确的是( )
A. |a|<|b| B. ad>0 C. a+c>0 D. d-a>0
4.若一个多边形的每个外角都是30°,则这个多边形的边数为
A. 6 B. 8 C. 10 D. 12
5.在一个不透明的袋子中,有1个白球和2个红球,它们只有颜色上的区别,从袋子中随机地摸出一个球记下颜色放回.再随机地摸出一个球.则两次都摸到白球的概率为( ).
A. B. C. D.
6.如图,直线a∥b,点B在直线a上,AB⊥BC,若∠1=40°,则∠2的度数为
A.40° B. 50°
C.80° D. 140°
7.,,三点在二次函数的图像上,则,,的大小关系为( )
A. B. C. D.
8.如图1,点从的顶点出发,沿匀速运动到点,图2是点运动时,线段的长度随时间变化的关系图象,其中是曲线部分的最低点,则的面积是
A. 30 B.60 C.78 D.156
二、填空题(共24分,每题3分)
9.若在实数范围内有意义,则x的取值范围是______.
10.已知,且m是整数,请写出一个符合要求的m的值 .
11.分解因式:______.
12.如图所示的网格是正方形网格,则=_____°(点A,B,P是网格线交点).
13.如图,AB为⊙O的直径,点P在AB的延长线上,PC,PD分别与⊙O相切于点C、D,若=40°,则的度数为 .
14.如图,反比例函数的图象经过点(2,1).当y<1时,x的取值范围是 .
15.如图,在矩形中,是边的中点,连结交对角线于点,若,则的长为__________.
16. 某工厂生产I号、II号两种产品,并将产品按照不同重量进行包装,已知包装产品款式有三种:A款,B款,C款,且三款包装的重量及所含I号、II号产品的重量如下表:
包装款式 包装的重量(吨) 含I号新产品的重量(吨) 含II号产品的重量(吨)
A款 6 3 3
B款 5 3 2
C款 5 2 3
现用一辆最大载重量为28吨的货车一次运送5个包装产品,且每种款式至少有1个.
(1)若恰好装运28吨包装产品,则装运方案中A款、B款、C款个数依次为 ;
(2)若装运的I号产品不超过13吨.同时装运的II号产品最多,则装运方案中A款、B款、C款的个数依次为 .(写出一种即可)
三、解答题(共60分,第17-18题,每题5分,第19-24题6分,第25-26题,每题7分)
17.计算: 18.解不等式组:
19.已知关于x的方程有两个实数根.
(1)求k的取值范围;
(2)当k取最大整数时,求此时方程的根.
20.我们把连接三角形两边中点的线段叫做三角形的中位线.三角形的中位线有如下性质:三角形的中位线平行于三角形的第三边并且等于第三边的一半.下面请对这个性质进行证明.
(1)如图1,点,分别是的边,的中点,求证:,且;
(2)如图2,点是边的中点,点是边的中点,若,,,直接写出的长=______.
21.在平面直角坐标系中,函数的图象经过点.
(1)求该函数的解析式;
(2)当时,对于x的每一个值,函数的值都小于函数的值,直接写出m的取值范围
(3)若反比例函数的图象与函数的图象交于点A,B.若,直接写出b的取值范围.
22.如图所示,△ABC中,∠ACB=90°,D,E分别为AB,BC的中点,连接DE并延长到点F,使得EF=DE,连接CD,CF,BF.
(1)求证:四边形BFCD是菱形;
(2)若,DE=5,求菱形BFCD的面积.
23.小明在“生活中的数学”探究活动中,经过市场调查,研究了某种商品的售价、销量、利润之间的变化关系.小明整理出该商品的相关数据如下表所示.
时间x(天) 1≤x<30 30≤x≤60
售价(元/件) x+40 70
每天销量(件) 100-2x
已知该商品的进价为每件10元,设销售该商品的每天利润为y元.
(1)求y与x的函数关系式;
(2)求销售该商品第几天时,当天销售利润最大,最大利润是多少?
24.如图,为⊙的直径,为⊙上一点,过点
作⊙的切线,过点作于点.
(1)求证:;
(2)若,,求的长.
25.在平面直角坐标系xOy中,抛物线与x轴的交点为点A(1,0)和点B.
(1)用含的式子表示;
(2)求抛物线的对称轴和点B的坐标;
(3)分别过点P(t,0)和点Q ( t+2, 0)作x轴的垂线,交抛物线于点M和点N,记抛物线在M,N之间的部分为图象G(包括M,N两点).记图形G上任意一点的纵坐标的最大值是m,最小值为n.
当a=1时,求m-n的最小值;
若存在实数t,使得m-n =1,直接写出a的取值范围.
26.在Rt△ABC中,∠ABC=90°,∠BAC=30°,D为边BC延长线上一动点,点E在边AC延长线上,CE=CD.点D关于点B的对称点为点F,连接AD,EF.
(1)设CD=a,BC=b.判断AE与CF的数量关系,并证明
(2)取AD中点P,连接PE、PF,补全图形,判断PE与PF的数量关系与位置关系,并证明.
同课章节目录
