山东省济宁市任城一中2013-2014学年高二下学期期中检测 数学文
文档属性
| 名称 | 山东省济宁市任城一中2013-2014学年高二下学期期中检测 数学文 |

|
|
| 格式 | zip | ||
| 文件大小 | 215.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-28 00:00:00 | ||
图片预览


文档简介
任城一中2013—2014学年高二下学期期中检测
数学(文)
一、选择题(本大题共12个小题,每个小题5分,共60分,每个小题只有一个正确答案,将正确答案填涂在答题卡的相应位置)
1.已知 EMBED Equation.DSMT4 ,则( )
A. B. C. D.
2.若复数 EMBED Equation.DSMT4 (a∈R,i是虚数单位)是纯虚数,则a的值为( )
A.-2 B.2 C.1 D.-1
3.已知命题p: x0≥0,使2x0=3,则p的否定是( )
A. x<0,使2x≠3
B. x0<0,使2x0≠3
C. x0≥0,使2x0≠3
D. x≥0,使2x≠3
4.若“0A.(-∞,0]∪[1,+∞) B.(-1,0)
C.[-1,0] D.(-∞,-1)∪(0,+∞)
5. 下列函数中,既是偶函数又在上单调递增的是( )
A. B.
C. D.
6. 设,,,……,,,则 ( )
A. B. C. D.
7. 根据给出的数塔猜测123 4569+7= ( )
19+2=11
129+3=111
1239+4=1 111
1 2349+5=11 111
12 3459+6=111 111
……
A.1 111 110 B.1 111 111
C.1 111 112 D.1 111 113
8.设是定义在R上的奇函数且单调递增,当时,恒成立,则实数的取值范围是( )
A. B. C. D.
9.已知函数,若在区间上单调递减,则实数的取值范围是( )
A. B. C. D.
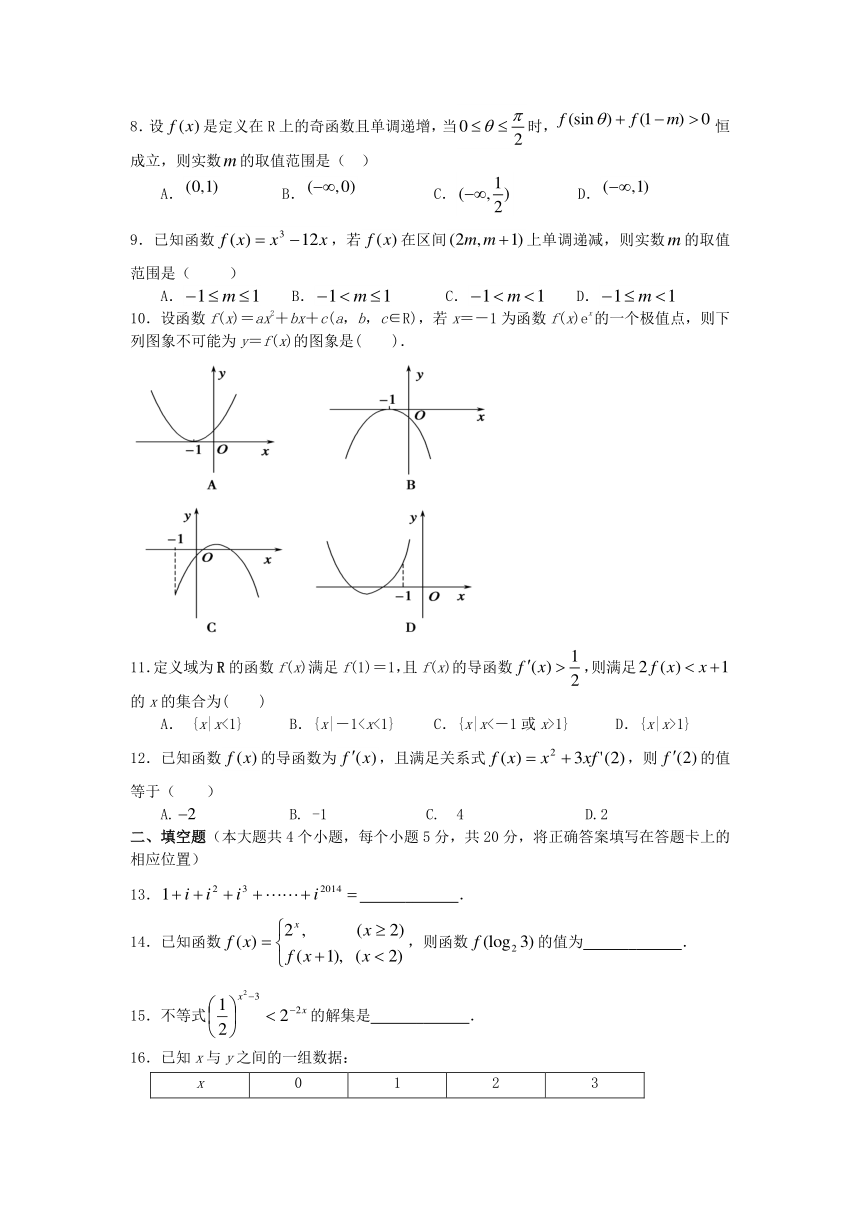
10.设函数f(x)=ax2+bx+c(a,b,c∈R),若x=-1为函数f(x)ex的一个极值点,则下列图象不可能为y=f(x)的图象是( ).
11.定义域为R的函数f(x)满足f(1)=1,且f(x)的导函数,则满足的x的集合为( )
A. {x|x<1} B.{x|-11} D.{x|x>1}
12.已知函数的导函数为,且满足关系式,则的值等于( )
A. B. -1 C. 4 D.2
二、填空题(本大题共4个小题,每个小题5分,共20分,将正确答案填写在答题卡上的相应位置)
13. .
14.已知函数,则函数的值为 .
15.不等式的解集是 .
16.已知x与y之间的一组数据:
x 0 1 2 3
y 1 3 5 7
则与的线性回归方程为必过点 .
三、解答题(本大题共6个小题,共70分,将解答过程填写在答题卡上的相应位置)
17.(本小题满分10分)
已知复数与都是纯虚数,求复数.
18.(本小题满分12分)
设函数.
(1)求的单调区间和极值;
(2)若关于的方程有3个不同实根,求实数a的取值范围.
19.(本小题满分12分)
设函数,其导函数为.
(1)若,求函数在点处的切线方程;
(2)求的单调区间;
(3)若为整数,若时,恒成立,试求的最大值.
20. (本小题满分12分)
设函数.
(1)若在时有极值,求实数的值和的极大值;
(2)若在定义域上是增函数,求实数的取值范围.
21.(本小题满分12分)
以下是某地搜集到的新房屋的销售价格(万元)和房屋的面积()的数据 ,若由资料可知对呈线性相关关系。
80 90 100 110 120
y 48 52 63 72 80
试求:(1)线性回归方程;
(2)根据(1)的结果估计当房屋面积为时的销售价格.
参考公式:
22.(本小题满分12分)
如图,椭圆上的点M与椭圆右焦点的连线与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
(1)求椭圆的离心率;
(2)过且与AB垂直的直线交椭圆于P、Q,
若的面积是20 ,求此时椭圆的方程.
参考答案:
1-5 CBDCD 6-10 CBDDD 11-12 AA
13. ; 14.;15. ; 16.
17.因为复数为纯虚数,所以设,
则=,
又由于是纯虚数,得,所以
18.(1),
令得:,
当变化时,的变化情况如下表:
0 0
增 极大 减 极小 增
所以的增区间是和,减区间是;
当时,取得极大值,极大值;
当时,取得极小值,极小值.
(2)由(1)得,作出函数的草图如图所示:
所以,实数的取值范围是.
19.(1)因为时,,所以,
故切线方程是
(2)的定义域为R,,
若在上单调递增;
若解得,
当变化时,变化如下表:
减 极小值 增
所以的单调减区间是:,增区间是:.
(3)即 ① ,
令则.
由(1)知,函数在单调递增,而,
所以在存在唯一的零点,故在存在唯一的零点,
且.
当时,;当时,,所以
.
又由,即得,所以,
这时.
由于①式等价,故整数k的最大值为2.
20.(1)∵在时有极值,∴有
又 ∴, ∴
∴有
由得,
又∴由得或
由得
∴在区间和上递增,在区间上递减
∴的极大值为
(2)若在定义域上是增函数,则在时恒成立
,
需时恒成立,
化为恒成立,
, 为所求。
21.(1)由已知数据表求得:,
将数据代入 计算得:b=0.84,
又由得:
线性回归方程为:.
(2)当时,求得(万元),
所以当房屋面积为时的销售价格为105万元
22.(1)易得
(2)设直线PQ的方程为 .代入椭圆方程消去x得:
,
整理得:
∴
因此a2=50,b2=25,所以椭圆方程为
数学(文)
一、选择题(本大题共12个小题,每个小题5分,共60分,每个小题只有一个正确答案,将正确答案填涂在答题卡的相应位置)
1.已知 EMBED Equation.DSMT4 ,则( )
A. B. C. D.
2.若复数 EMBED Equation.DSMT4 (a∈R,i是虚数单位)是纯虚数,则a的值为( )
A.-2 B.2 C.1 D.-1
3.已知命题p: x0≥0,使2x0=3,则p的否定是( )
A. x<0,使2x≠3
B. x0<0,使2x0≠3
C. x0≥0,使2x0≠3
D. x≥0,使2x≠3
4.若“0
C.[-1,0] D.(-∞,-1)∪(0,+∞)
5. 下列函数中,既是偶函数又在上单调递增的是( )
A. B.
C. D.
6. 设,,,……,,,则 ( )
A. B. C. D.
7. 根据给出的数塔猜测123 4569+7= ( )
19+2=11
129+3=111
1239+4=1 111
1 2349+5=11 111
12 3459+6=111 111
……
A.1 111 110 B.1 111 111
C.1 111 112 D.1 111 113
8.设是定义在R上的奇函数且单调递增,当时,恒成立,则实数的取值范围是( )
A. B. C. D.
9.已知函数,若在区间上单调递减,则实数的取值范围是( )
A. B. C. D.
10.设函数f(x)=ax2+bx+c(a,b,c∈R),若x=-1为函数f(x)ex的一个极值点,则下列图象不可能为y=f(x)的图象是( ).
11.定义域为R的函数f(x)满足f(1)=1,且f(x)的导函数,则满足的x的集合为( )
A. {x|x<1} B.{x|-1
12.已知函数的导函数为,且满足关系式,则的值等于( )
A. B. -1 C. 4 D.2
二、填空题(本大题共4个小题,每个小题5分,共20分,将正确答案填写在答题卡上的相应位置)
13. .
14.已知函数,则函数的值为 .
15.不等式的解集是 .
16.已知x与y之间的一组数据:
x 0 1 2 3
y 1 3 5 7
则与的线性回归方程为必过点 .
三、解答题(本大题共6个小题,共70分,将解答过程填写在答题卡上的相应位置)
17.(本小题满分10分)
已知复数与都是纯虚数,求复数.
18.(本小题满分12分)
设函数.
(1)求的单调区间和极值;
(2)若关于的方程有3个不同实根,求实数a的取值范围.
19.(本小题满分12分)
设函数,其导函数为.
(1)若,求函数在点处的切线方程;
(2)求的单调区间;
(3)若为整数,若时,恒成立,试求的最大值.
20. (本小题满分12分)
设函数.
(1)若在时有极值,求实数的值和的极大值;
(2)若在定义域上是增函数,求实数的取值范围.
21.(本小题满分12分)
以下是某地搜集到的新房屋的销售价格(万元)和房屋的面积()的数据 ,若由资料可知对呈线性相关关系。
80 90 100 110 120
y 48 52 63 72 80
试求:(1)线性回归方程;
(2)根据(1)的结果估计当房屋面积为时的销售价格.
参考公式:
22.(本小题满分12分)
如图,椭圆上的点M与椭圆右焦点的连线与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
(1)求椭圆的离心率;
(2)过且与AB垂直的直线交椭圆于P、Q,
若的面积是20 ,求此时椭圆的方程.
参考答案:
1-5 CBDCD 6-10 CBDDD 11-12 AA
13. ; 14.;15. ; 16.
17.因为复数为纯虚数,所以设,
则=,
又由于是纯虚数,得,所以
18.(1),
令得:,
当变化时,的变化情况如下表:
0 0
增 极大 减 极小 增
所以的增区间是和,减区间是;
当时,取得极大值,极大值;
当时,取得极小值,极小值.
(2)由(1)得,作出函数的草图如图所示:
所以,实数的取值范围是.
19.(1)因为时,,所以,
故切线方程是
(2)的定义域为R,,
若在上单调递增;
若解得,
当变化时,变化如下表:
减 极小值 增
所以的单调减区间是:,增区间是:.
(3)即 ① ,
令则.
由(1)知,函数在单调递增,而,
所以在存在唯一的零点,故在存在唯一的零点,
且.
当时,;当时,,所以
.
又由,即得,所以,
这时.
由于①式等价,故整数k的最大值为2.
20.(1)∵在时有极值,∴有
又 ∴, ∴
∴有
由得,
又∴由得或
由得
∴在区间和上递增,在区间上递减
∴的极大值为
(2)若在定义域上是增函数,则在时恒成立
,
需时恒成立,
化为恒成立,
, 为所求。
21.(1)由已知数据表求得:,
将数据代入 计算得:b=0.84,
又由得:
线性回归方程为:.
(2)当时,求得(万元),
所以当房屋面积为时的销售价格为105万元
22.(1)易得
(2)设直线PQ的方程为 .代入椭圆方程消去x得:
,
整理得:
∴
因此a2=50,b2=25,所以椭圆方程为
同课章节目录
