18.2.2菱形 强化练习(含答案)数学人教版八年级下册
文档属性
| 名称 | 18.2.2菱形 强化练习(含答案)数学人教版八年级下册 |
|
|
| 格式 | zip | ||
| 文件大小 | 567.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 00:00:00 | ||
图片预览




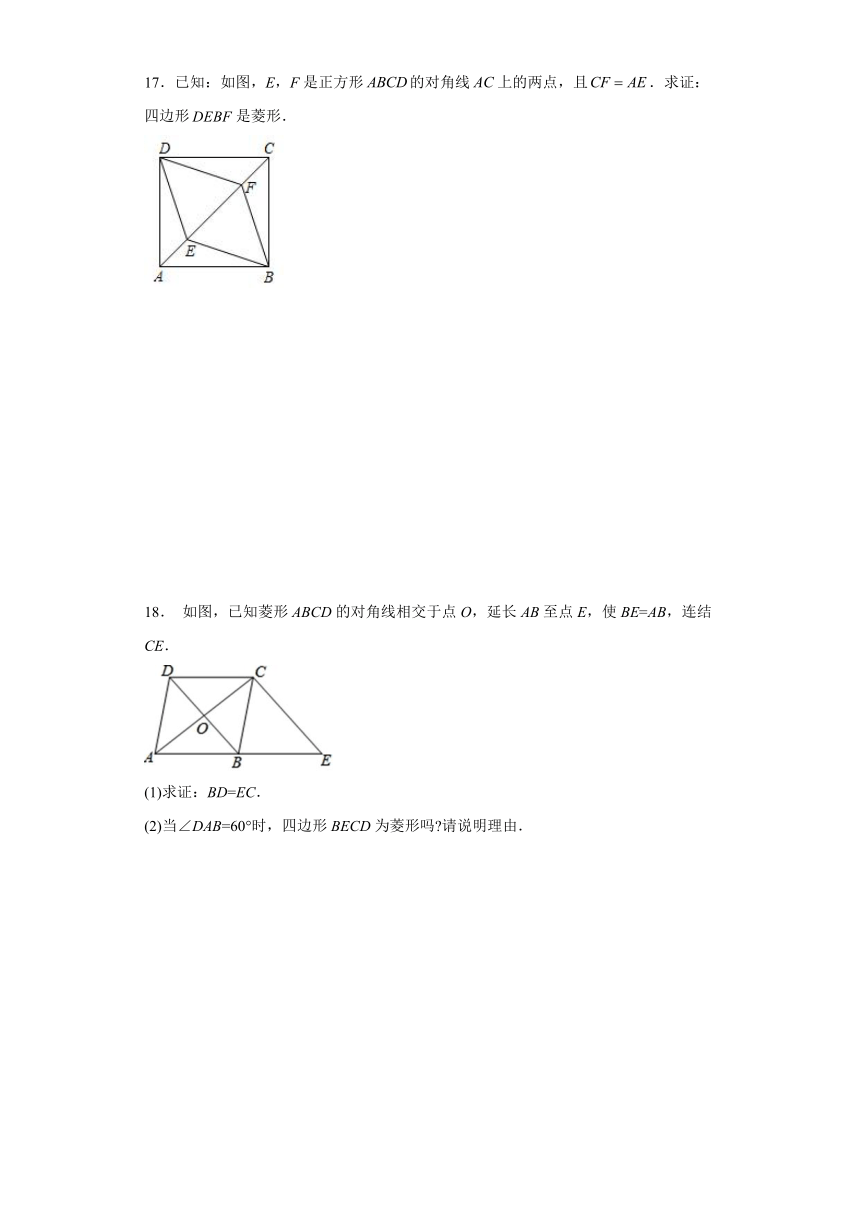
文档简介
18.2.2菱形 强化练习
一、单选题
1.已知菱形的两条对角线的长分别是和,则菱形的面积是( )
A. B. C. D.
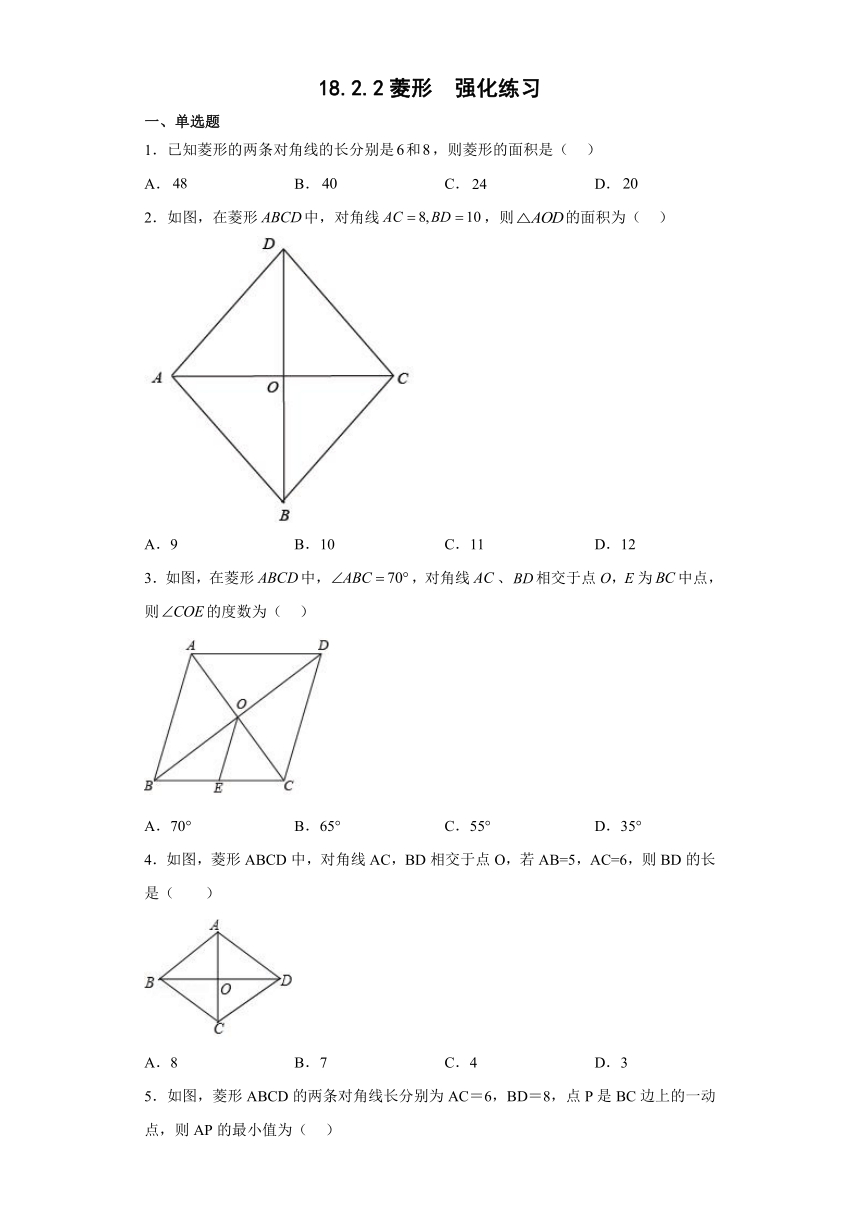
2.如图,在菱形中,对角线,则的面积为( )
A.9 B.10 C.11 D.12
3.如图,在菱形中,,对角线、相交于点O,E为中点,则的度数为( )
A.70° B.65° C.55° D.35°
4.如图,菱形ABCD中,对角线AC,BD相交于点O,若AB=5,AC=6,则BD的长是( )
A.8 B.7 C.4 D.3
5.如图,菱形ABCD的两条对角线长分别为AC=6,BD=8,点P是BC边上的一动点,则AP的最小值为( )
A.4 B.4.8 C.5 D.5.5
6.如图,已知某菱形花坛的周长是,,则花坛对角线的长是( )
A. B. C. D.
7.在如图所示的纸片中,,D是斜边AB的中点,把纸片沿着CD折叠,点B到点E的位置,连接AE.若,,则等于( )
A. B. C. D.
8.如图,在菱形中,,,E,F分别是边上的动点,连接和,G,H分别为,的中点,连接,则的最小值为( )
A. B. C. D.1
9.如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点.下列三种说法:
① .四边形EFGH一定是平行四边形;
②.若AC=BD,则四边形EFGH 是菱形;
③.若AC⊥BD,则四边形EFGH是矩形.
其中正确的是( )
A.① B.①② C.①③ D.①②③
10.已知的长,宽,如图①,将沿着AE折叠,折叠后点B落在AD边上,对应点为F,沿EF剪下四边形ABEF(称为第一次操作);如图②,再把剩下的四边形FECD沿着EN折叠,折叠后点C落在EF边上,对应点为M,沿MN剪下四边形MECN(称为第二次操作);将剩下的四边形FMND如此反复操作下去,若在第n次操作后,剩下的四边形为菱形,则操作停止.当时,a的值为( )
A. B.15 C. D.或
二、填空题
11.如图,在菱形中,,,分别为,的中点,是对角线上的一个动点,则的最小值是________.
12.菱形中,,这个菱形的周长是28,则的长是:______.
13.如图,菱形中,,则_____.
14.如图,长方形中,E为的中点,将沿直线折叠时点B落在点F处,连接,若,则___________度.
15.如图,边长为6的菱形ABCD中,AC是其对角线,∠B=60°,点P在CD上,CP=2,点M在AD上,点N在AC上,则△PMN的周长的最小值为_____________ .
三、解答题
16.如图,四边形是菱形,对角线与相交于点,,.求的长(结果保留根号).
17.已知:如图,E,F是正方形的对角线上的两点,且.求证:四边形是菱形.
18. 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC.
(2)当∠DAB=60°时,四边形BECD为菱形吗 请说明理由.
19.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)试连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.
20.如图,在四边形ABCD中,ADBC,对角线BD的垂直平分线与边AD、BC分别相交于点M、N.
(1)求证:四边形BNDM是菱形;
(2)若∠C=90°,BC=16,CD=8,求菱形BNDM的周长.
参考答案
1.C
2.B
3.C
4.A
5.B
6.B
7.B
8.B
9.D
10.A
11.10
12.
13.
14.37
15.2
16.证明:∵四边形是菱形,
在中,,
∴,
在中,,
∴,
∴.
17.解:证明:连接BD交AC于点O,
∵ABCD是正方形,
∴AP=CO,BO=DO,AC⊥BD,
∴OF=OE,
∴四边形DEBF是菱形.
18.(1)证明:四边形ABCD是菱形,
∴AB=CD,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD 是平行四边形,
∴BD=EC;
(2)解:结论:四边形BECD是菱形.
理由:∵四边形ABCD是菱形,
∴AD=AB,
∵∠DAB=60°,
∴△ADB,△DCB都是等边三角形,
∴DC=DB,
∵四边形BECD是平行四边形,
∴四边形BECD是菱形.
19.(1)证明:四边形是平行四边形,
,,
,
,
在和中,
.
(2)当平分时,四边形是菱形.
理由:如图 ,连接AF,CE,
平分,
,
四边形是平行四边形,
,,,
,
,
,
平行四边形是菱形,
,
,
,
.
又,
四边形是平行四边形,
,
四边形是菱形.
20.(1)证明:∵AD∥BC
∴∠DMO=∠BNO
∵MN是对角线BD的垂直平分线
∴OB=OD,MN⊥BD
在△MOD和△NOB中
∴△MOD≌△NOB(AAS)
∴OM=ON
∵OB=OD
∴四边形BNDM是平行四边形
∵MN⊥BD
∴平行四边形BNDM是菱形.
(2)解:∵四边形BNDM是菱形
∴BM=BN=DM=DN
设BN=DN=x,则CN=BC﹣BN=16﹣x
在Rt△CDN中,由勾股定理得:CD2+CN2=DN2
即82+(16﹣x)2=x2
解得:x=10
即BN=10
∴菱形BNDM的周长=4BN=40.
一、单选题
1.已知菱形的两条对角线的长分别是和,则菱形的面积是( )
A. B. C. D.
2.如图,在菱形中,对角线,则的面积为( )
A.9 B.10 C.11 D.12
3.如图,在菱形中,,对角线、相交于点O,E为中点,则的度数为( )
A.70° B.65° C.55° D.35°
4.如图,菱形ABCD中,对角线AC,BD相交于点O,若AB=5,AC=6,则BD的长是( )
A.8 B.7 C.4 D.3
5.如图,菱形ABCD的两条对角线长分别为AC=6,BD=8,点P是BC边上的一动点,则AP的最小值为( )
A.4 B.4.8 C.5 D.5.5
6.如图,已知某菱形花坛的周长是,,则花坛对角线的长是( )
A. B. C. D.
7.在如图所示的纸片中,,D是斜边AB的中点,把纸片沿着CD折叠,点B到点E的位置,连接AE.若,,则等于( )
A. B. C. D.
8.如图,在菱形中,,,E,F分别是边上的动点,连接和,G,H分别为,的中点,连接,则的最小值为( )
A. B. C. D.1
9.如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点.下列三种说法:
① .四边形EFGH一定是平行四边形;
②.若AC=BD,则四边形EFGH 是菱形;
③.若AC⊥BD,则四边形EFGH是矩形.
其中正确的是( )
A.① B.①② C.①③ D.①②③
10.已知的长,宽,如图①,将沿着AE折叠,折叠后点B落在AD边上,对应点为F,沿EF剪下四边形ABEF(称为第一次操作);如图②,再把剩下的四边形FECD沿着EN折叠,折叠后点C落在EF边上,对应点为M,沿MN剪下四边形MECN(称为第二次操作);将剩下的四边形FMND如此反复操作下去,若在第n次操作后,剩下的四边形为菱形,则操作停止.当时,a的值为( )
A. B.15 C. D.或
二、填空题
11.如图,在菱形中,,,分别为,的中点,是对角线上的一个动点,则的最小值是________.
12.菱形中,,这个菱形的周长是28,则的长是:______.
13.如图,菱形中,,则_____.
14.如图,长方形中,E为的中点,将沿直线折叠时点B落在点F处,连接,若,则___________度.
15.如图,边长为6的菱形ABCD中,AC是其对角线,∠B=60°,点P在CD上,CP=2,点M在AD上,点N在AC上,则△PMN的周长的最小值为_____________ .
三、解答题
16.如图,四边形是菱形,对角线与相交于点,,.求的长(结果保留根号).
17.已知:如图,E,F是正方形的对角线上的两点,且.求证:四边形是菱形.
18. 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC.
(2)当∠DAB=60°时,四边形BECD为菱形吗 请说明理由.
19.如图,在 ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.
(1)求证:△ADE≌△CBF;
(2)试连接AF,CE.当BD平分∠ABC时,四边形AFCE是什么特殊四边形?请说明理由.
20.如图,在四边形ABCD中,ADBC,对角线BD的垂直平分线与边AD、BC分别相交于点M、N.
(1)求证:四边形BNDM是菱形;
(2)若∠C=90°,BC=16,CD=8,求菱形BNDM的周长.
参考答案
1.C
2.B
3.C
4.A
5.B
6.B
7.B
8.B
9.D
10.A
11.10
12.
13.
14.37
15.2
16.证明:∵四边形是菱形,
在中,,
∴,
在中,,
∴,
∴.
17.解:证明:连接BD交AC于点O,
∵ABCD是正方形,
∴AP=CO,BO=DO,AC⊥BD,
∴OF=OE,
∴四边形DEBF是菱形.
18.(1)证明:四边形ABCD是菱形,
∴AB=CD,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD 是平行四边形,
∴BD=EC;
(2)解:结论:四边形BECD是菱形.
理由:∵四边形ABCD是菱形,
∴AD=AB,
∵∠DAB=60°,
∴△ADB,△DCB都是等边三角形,
∴DC=DB,
∵四边形BECD是平行四边形,
∴四边形BECD是菱形.
19.(1)证明:四边形是平行四边形,
,,
,
,
在和中,
.
(2)当平分时,四边形是菱形.
理由:如图 ,连接AF,CE,
平分,
,
四边形是平行四边形,
,,,
,
,
,
平行四边形是菱形,
,
,
,
.
又,
四边形是平行四边形,
,
四边形是菱形.
20.(1)证明:∵AD∥BC
∴∠DMO=∠BNO
∵MN是对角线BD的垂直平分线
∴OB=OD,MN⊥BD
在△MOD和△NOB中
∴△MOD≌△NOB(AAS)
∴OM=ON
∵OB=OD
∴四边形BNDM是平行四边形
∵MN⊥BD
∴平行四边形BNDM是菱形.
(2)解:∵四边形BNDM是菱形
∴BM=BN=DM=DN
设BN=DN=x,则CN=BC﹣BN=16﹣x
在Rt△CDN中,由勾股定理得:CD2+CN2=DN2
即82+(16﹣x)2=x2
解得:x=10
即BN=10
∴菱形BNDM的周长=4BN=40.
