人教版 数学 六年级下册 第六单元第3课时《式与方程》精品课件(共27张ppt)
文档属性
| 名称 | 人教版 数学 六年级下册 第六单元第3课时《式与方程》精品课件(共27张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-16 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
式与方程
第六单元 整理和复习
输入标题
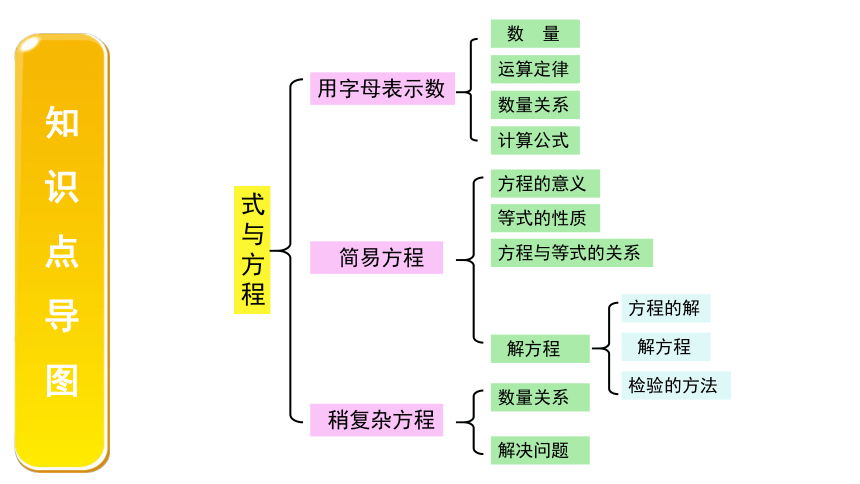
知识点导图
式与方程
用字母表示数
方程的解
解方程
简易方程
等式的性质
方程的意义
检验的方法
运算定律
方程与等式的关系
解方程
计算公式
数量关系
数 量
稍复杂方程
解决问题
数量关系
综合练习
知识梳理
拓展练习
课堂小结
布置作业
计算下面左右两组算式,然后回答问题。
22-12= (2+1)×(2-1)=
92-32= (9+3)×(9-3)=
112-52= (11+5)×(11-5)=
3
3
72
72
96
96
左边的算式和右边算式的结果相等。
通过计算,你有什么发现?
练习回顾 导入复习
综合练习
知识梳理
拓展练习
课堂小结
布置作业
计算下面左右两组算式,然后回答问题。
22-12= (2+1)×(2-1)=
92-32= (9+3)×(9-3)=
112-52= (11+5)×(11-5)=
3
3
72
72
96
96
再写一个这样的算式,使左右两边的结果相等?
0.32-0.12=0.08
练习回顾 导入复习
(0.3+0.1)×(0.3-0.1)=0.08
0.32-0.12=(0.3+0.1)×(0.3-0.1)
综合练习
知识梳理
拓展练习
课堂小结
布置作业
计算下面左右两组算式,然后回答问题。
22-12= (2+1)×(2-1)=
92-32= (9+3)×(9-3)=
112-52= (11+5)×(11-5)=
3
3
72
72
96
96
你能用字母表示你的发现吗?
用字母a、b表示任意两个数,那么 a2-b2=(a+b)×(a-b)。
练习回顾 导入复习
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
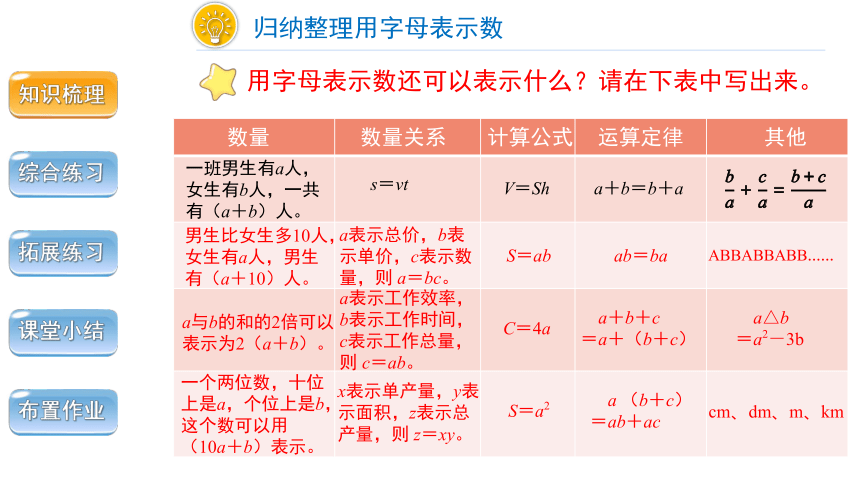
数量
s=vt
一班男生有a人,女生有b人,一共有(a+b)人。
数量关系
计算公式
运算定律
其他
V=Sh
a+b=b+a
S=ab
C=4a
S=a2
ab=ba
a (b+c)
=ab+ac
a+b+c
=a+(b+c)
ABBABBABB……
a表示总价,b表示单价,c表示数量,则 a=bc。
a表示工作效率,b表示工作时间,c表示工作总量,则 c=ab。
x表示单产量,y表示面积,z表示总产量,则 z=xy。
男生比女生多10人,女生有a人,男生有(a+10)人。
a△b
=a2-3b
一个两位数,十位上是a,个位上是b,这个数可以用(10a+b)表示。
a与b的和的2倍可以表示为2(a+b)。
cm、dm、m、km
用字母表示数还可以表示什么?请在下表中写出来。
归纳整理用字母表示数
一级标题
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
想一想,在一个含有字母的式子里,数与字母、字母与字母相乘,书写时应注意什么?
当数和字母、字母和字母相乘时,中间的乘号可以记作“·”,也可以省略不写。
省略乘号时,应该把数写在字母的前面。
“1”与任何字母相乘时,“1”省略不写。
归纳整理用字母表示数
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
① 2.5-x<10
④ x÷2=10
⑥ 4+0.7x=102
② 2a÷9
⑤ 2y-x>12
③ +y=6
③ 、 ④ 、⑥是方程。
下面的式子中哪些是方程?
练习回顾 复习方程的概念
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
方程
等式
含有未知数的等式就是方程。
想一想:什么是方程?它与等式有什么区别和联系?
可以用这样图表示它们之间的关系:
方程一定是等式,等式不一定是方程。
练习回顾 复习方程的概念
x÷2=10
4+0.7x=102
+y=6
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
解:+y-=6-
y=5
解:x÷2×2=10×2
x=20
解:4+0.7x-4=102-4
0.7x=98
0.7x÷0.7=98÷0.7
x=140
解一解下面的方程。
x÷2=10
4+0.7x=102
+y=6
练习回顾 解方程
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
解:+y-=6-
y=5
解:x÷2×2=10×2
x=20
解:4+0.7x-4=102-4
0.7x=98
0.7x÷0.7=98÷0.7
x=140
想一想:解方程的依据是什么?
等式性质1:等式两边加上或减去同一个数,左右两边仍然相等。
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
练习回顾 解方程的依据
x÷2=10
4+0.7x=102
+y=6
小芳在踢毽比赛中踢了42下,她踢毽的数量是小云的。
小云踢了多少下?
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
解:设小云踢了x下。
x=42
x=42×
小云踢的数量× =小芳踢的数量
x÷=42÷
x=56
答:小云踢了56下。
用方程解决问题。
复习用方程解决问题
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
2.分析实际问题中的数量关系,找出等量关系。
4.解方程,并检验作答。
1.找出未知量,用字母x表示。
3.根据等量关系,列出方程。
用方程解决实际问题有哪些步骤?
梳理用方程解决问题的一般步骤
a的
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
复习巩固用字母表示数
1.连线。
比a多3的数
比a少3的数
3个a相加的和
3个a相乘的积
a的3倍
a3
3a
a+3
a-3
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
复习巩固用字母表示数
(1)你能发现什么规律?如果摆n个正方形,
需要( )根小棒。
规律:摆1个正方形需要4根小棒,
以后每多摆1个正方形就增加3根小棒。
3n+1
2.用小棒摆正方形,如下图所示。
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
复习巩固用字母表示数
(2)摆150个正方形, 需要( )根小棒。
当n=150时,3n+1=3×150+1=451(根)。
451
2.用小棒摆正方形,如下图所示。
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
复习巩固解方程
x-0.25=
=30%
x=1.2
解:x-0.25+0.25=0.25
x=+0.25
x=+
x=+
x=
解:×4=0.3×4
3.解方程,带 的要验算。
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
复习巩固解方程
x+x=42
=24+18
x=36
检验:方程左边=×36+×36
=42
=方程右边
所以,x=36是方程的解。
注意方程检验的格式!
解x+x=42
x=42
x=42×
x÷=42÷
3.解方程,带 的要验算。
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
复习巩固用方程解决问题
4.用方程解决问题。
(1)绿化队为一个居民社区栽花。栽月季花240棵,再加上16棵就是所栽丁香花棵数的2倍。栽了多少棵丁香花?
丁香花棵数×2=月季花棵数+16
解:设栽了x棵丁香花。
2x=240+16
x=128
2x=256
x=256÷2
答:栽了128棵丁香花。
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
复习巩固用方程解决问题
(2)阳阳正在读一本科普书,第一周读了90页,还剩下这本书的没有读。这本科普书一共多少页?
解:设这本科普书一共 x 页。
(1-)x=90
总页数×(1-)=第一周读的页数
x÷=90÷
x=135
x=90×
答:这本科普书一共135页。
4.用方程解决问题。
x=90
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
复习巩固用方程解决问题
5.你知道吗?鞋的尺码一般用“码”或“厘米”作单位,它们之间的换算关系是:b=2a-10,其中b表示码数,a表示厘米数,根据这个关系,填出球球一家所穿鞋的尺码情况。
爸爸的鞋 妈妈的鞋 球球的鞋 你穿的鞋
a 23
b 42 37
42=2a-10
26
23.5
37=2a-10
b=2×23-10
36
22.5
35
输入标题
课堂小结
布置作业
知识梳理
拓展练习
综合练习
拓展提升用字母表示数
(1)三个连续的自然数,中间的数是a,则a的前边和后边分别是( )和( )。
a的前边的数比a小1,a的后边的数比a大1。
a+1
a-1
1.填空。
(2)三个连续奇数的平均数是a,其中最大的是( ),最小的是( )。
a
中间的数
a+2
最大的数
比a大2
a+2
a-2
最小的数
比a小2
a-2
输入标题
课堂小结
布置作业
知识梳理
拓展练习
综合练习
拓展提升用方程解决问题
2.一个笼子里有8条腿的蜘蛛和6条腿的蚱蜢共25只。如果它们的总腿数有170条,那么蜘蛛和蚱蜢各有多少只?
蜘蛛腿的数量+蚱蜢腿的数量=总腿数
解:设蜘蛛有x只,蚱蜢有(25-x)只。
8x+(25-x)×6=170
8x+150-6x=170
2x+150=170
2x+150-150=170-150
2x=20
x=10
答:蜘蛛有10只,蚱蜢有15只。
25-10=15(只)
蜘蛛的数量+蚱蜢的数量=总只数
输入标题
课堂小结
布置作业
知识梳理
拓展练习
综合练习
拓展提升用方程解决问题
3.小伟和小明原有图书本数的比是1∶5,后来小明给小伟1本图书,这时小伟与小明图书本数的比是1∶4。小伟与小明原来各有图书多少本?
解:设小伟原有x本,则小明原有5x本。
(x+1)∶(5x-1)=1∶4
5x-1=4(x+1)
5x-1=4x+4
5x-1-4x=4x+4-4x
x-1=4
x=5
答:小伟原有5本,小明原有25本。
5×5=25(本)
一级标题
输入标题
布置作业
创设情境
巩固练习
课堂小结
探究新知
你有什么收获?
用字母表示数可以表示数量、数量关系、计算公式、运算定律等。
能够结合具体情境找到等量关系,并利用方程解决问题。
一级标题
输入标题
知识梳理
拓展练习
课堂小结
布置作业
综合练习
教材P82~P83
第1、2、3、7、8、11、12、13题
再见
式与方程
第六单元 整理和复习
输入标题
知识点导图
式与方程
用字母表示数
方程的解
解方程
简易方程
等式的性质
方程的意义
检验的方法
运算定律
方程与等式的关系
解方程
计算公式
数量关系
数 量
稍复杂方程
解决问题
数量关系
综合练习
知识梳理
拓展练习
课堂小结
布置作业
计算下面左右两组算式,然后回答问题。
22-12= (2+1)×(2-1)=
92-32= (9+3)×(9-3)=
112-52= (11+5)×(11-5)=
3
3
72
72
96
96
左边的算式和右边算式的结果相等。
通过计算,你有什么发现?
练习回顾 导入复习
综合练习
知识梳理
拓展练习
课堂小结
布置作业
计算下面左右两组算式,然后回答问题。
22-12= (2+1)×(2-1)=
92-32= (9+3)×(9-3)=
112-52= (11+5)×(11-5)=
3
3
72
72
96
96
再写一个这样的算式,使左右两边的结果相等?
0.32-0.12=0.08
练习回顾 导入复习
(0.3+0.1)×(0.3-0.1)=0.08
0.32-0.12=(0.3+0.1)×(0.3-0.1)
综合练习
知识梳理
拓展练习
课堂小结
布置作业
计算下面左右两组算式,然后回答问题。
22-12= (2+1)×(2-1)=
92-32= (9+3)×(9-3)=
112-52= (11+5)×(11-5)=
3
3
72
72
96
96
你能用字母表示你的发现吗?
用字母a、b表示任意两个数,那么 a2-b2=(a+b)×(a-b)。
练习回顾 导入复习
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
数量
s=vt
一班男生有a人,女生有b人,一共有(a+b)人。
数量关系
计算公式
运算定律
其他
V=Sh
a+b=b+a
S=ab
C=4a
S=a2
ab=ba
a (b+c)
=ab+ac
a+b+c
=a+(b+c)
ABBABBABB……
a表示总价,b表示单价,c表示数量,则 a=bc。
a表示工作效率,b表示工作时间,c表示工作总量,则 c=ab。
x表示单产量,y表示面积,z表示总产量,则 z=xy。
男生比女生多10人,女生有a人,男生有(a+10)人。
a△b
=a2-3b
一个两位数,十位上是a,个位上是b,这个数可以用(10a+b)表示。
a与b的和的2倍可以表示为2(a+b)。
cm、dm、m、km
用字母表示数还可以表示什么?请在下表中写出来。
归纳整理用字母表示数
一级标题
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
想一想,在一个含有字母的式子里,数与字母、字母与字母相乘,书写时应注意什么?
当数和字母、字母和字母相乘时,中间的乘号可以记作“·”,也可以省略不写。
省略乘号时,应该把数写在字母的前面。
“1”与任何字母相乘时,“1”省略不写。
归纳整理用字母表示数
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
① 2.5-x<10
④ x÷2=10
⑥ 4+0.7x=102
② 2a÷9
⑤ 2y-x>12
③ +y=6
③ 、 ④ 、⑥是方程。
下面的式子中哪些是方程?
练习回顾 复习方程的概念
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
方程
等式
含有未知数的等式就是方程。
想一想:什么是方程?它与等式有什么区别和联系?
可以用这样图表示它们之间的关系:
方程一定是等式,等式不一定是方程。
练习回顾 复习方程的概念
x÷2=10
4+0.7x=102
+y=6
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
解:+y-=6-
y=5
解:x÷2×2=10×2
x=20
解:4+0.7x-4=102-4
0.7x=98
0.7x÷0.7=98÷0.7
x=140
解一解下面的方程。
x÷2=10
4+0.7x=102
+y=6
练习回顾 解方程
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
解:+y-=6-
y=5
解:x÷2×2=10×2
x=20
解:4+0.7x-4=102-4
0.7x=98
0.7x÷0.7=98÷0.7
x=140
想一想:解方程的依据是什么?
等式性质1:等式两边加上或减去同一个数,左右两边仍然相等。
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
练习回顾 解方程的依据
x÷2=10
4+0.7x=102
+y=6
小芳在踢毽比赛中踢了42下,她踢毽的数量是小云的。
小云踢了多少下?
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
解:设小云踢了x下。
x=42
x=42×
小云踢的数量× =小芳踢的数量
x÷=42÷
x=56
答:小云踢了56下。
用方程解决问题。
复习用方程解决问题
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
2.分析实际问题中的数量关系,找出等量关系。
4.解方程,并检验作答。
1.找出未知量,用字母x表示。
3.根据等量关系,列出方程。
用方程解决实际问题有哪些步骤?
梳理用方程解决问题的一般步骤
a的
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
复习巩固用字母表示数
1.连线。
比a多3的数
比a少3的数
3个a相加的和
3个a相乘的积
a的3倍
a3
3a
a+3
a-3
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
复习巩固用字母表示数
(1)你能发现什么规律?如果摆n个正方形,
需要( )根小棒。
规律:摆1个正方形需要4根小棒,
以后每多摆1个正方形就增加3根小棒。
3n+1
2.用小棒摆正方形,如下图所示。
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
复习巩固用字母表示数
(2)摆150个正方形, 需要( )根小棒。
当n=150时,3n+1=3×150+1=451(根)。
451
2.用小棒摆正方形,如下图所示。
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
复习巩固解方程
x-0.25=
=30%
x=1.2
解:x-0.25+0.25=0.25
x=+0.25
x=+
x=+
x=
解:×4=0.3×4
3.解方程,带 的要验算。
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
复习巩固解方程
x+x=42
=24+18
x=36
检验:方程左边=×36+×36
=42
=方程右边
所以,x=36是方程的解。
注意方程检验的格式!
解x+x=42
x=42
x=42×
x÷=42÷
3.解方程,带 的要验算。
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
复习巩固用方程解决问题
4.用方程解决问题。
(1)绿化队为一个居民社区栽花。栽月季花240棵,再加上16棵就是所栽丁香花棵数的2倍。栽了多少棵丁香花?
丁香花棵数×2=月季花棵数+16
解:设栽了x棵丁香花。
2x=240+16
x=128
2x=256
x=256÷2
答:栽了128棵丁香花。
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
复习巩固用方程解决问题
(2)阳阳正在读一本科普书,第一周读了90页,还剩下这本书的没有读。这本科普书一共多少页?
解:设这本科普书一共 x 页。
(1-)x=90
总页数×(1-)=第一周读的页数
x÷=90÷
x=135
x=90×
答:这本科普书一共135页。
4.用方程解决问题。
x=90
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
复习巩固用方程解决问题
5.你知道吗?鞋的尺码一般用“码”或“厘米”作单位,它们之间的换算关系是:b=2a-10,其中b表示码数,a表示厘米数,根据这个关系,填出球球一家所穿鞋的尺码情况。
爸爸的鞋 妈妈的鞋 球球的鞋 你穿的鞋
a 23
b 42 37
42=2a-10
26
23.5
37=2a-10
b=2×23-10
36
22.5
35
输入标题
课堂小结
布置作业
知识梳理
拓展练习
综合练习
拓展提升用字母表示数
(1)三个连续的自然数,中间的数是a,则a的前边和后边分别是( )和( )。
a的前边的数比a小1,a的后边的数比a大1。
a+1
a-1
1.填空。
(2)三个连续奇数的平均数是a,其中最大的是( ),最小的是( )。
a
中间的数
a+2
最大的数
比a大2
a+2
a-2
最小的数
比a小2
a-2
输入标题
课堂小结
布置作业
知识梳理
拓展练习
综合练习
拓展提升用方程解决问题
2.一个笼子里有8条腿的蜘蛛和6条腿的蚱蜢共25只。如果它们的总腿数有170条,那么蜘蛛和蚱蜢各有多少只?
蜘蛛腿的数量+蚱蜢腿的数量=总腿数
解:设蜘蛛有x只,蚱蜢有(25-x)只。
8x+(25-x)×6=170
8x+150-6x=170
2x+150=170
2x+150-150=170-150
2x=20
x=10
答:蜘蛛有10只,蚱蜢有15只。
25-10=15(只)
蜘蛛的数量+蚱蜢的数量=总只数
输入标题
课堂小结
布置作业
知识梳理
拓展练习
综合练习
拓展提升用方程解决问题
3.小伟和小明原有图书本数的比是1∶5,后来小明给小伟1本图书,这时小伟与小明图书本数的比是1∶4。小伟与小明原来各有图书多少本?
解:设小伟原有x本,则小明原有5x本。
(x+1)∶(5x-1)=1∶4
5x-1=4(x+1)
5x-1=4x+4
5x-1-4x=4x+4-4x
x-1=4
x=5
答:小伟原有5本,小明原有25本。
5×5=25(本)
一级标题
输入标题
布置作业
创设情境
巩固练习
课堂小结
探究新知
你有什么收获?
用字母表示数可以表示数量、数量关系、计算公式、运算定律等。
能够结合具体情境找到等量关系,并利用方程解决问题。
一级标题
输入标题
知识梳理
拓展练习
课堂小结
布置作业
综合练习
教材P82~P83
第1、2、3、7、8、11、12、13题
再见
