部编版 数学 六年级下册 第六单元第11课时《数学思考》精品课件(共30张ppt)
文档属性
| 名称 | 部编版 数学 六年级下册 第六单元第11课时《数学思考》精品课件(共30张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 896.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-16 00:00:00 | ||
图片预览





文档简介
(共30张PPT)
数学思考
第六单元 整理和复习
输入标题
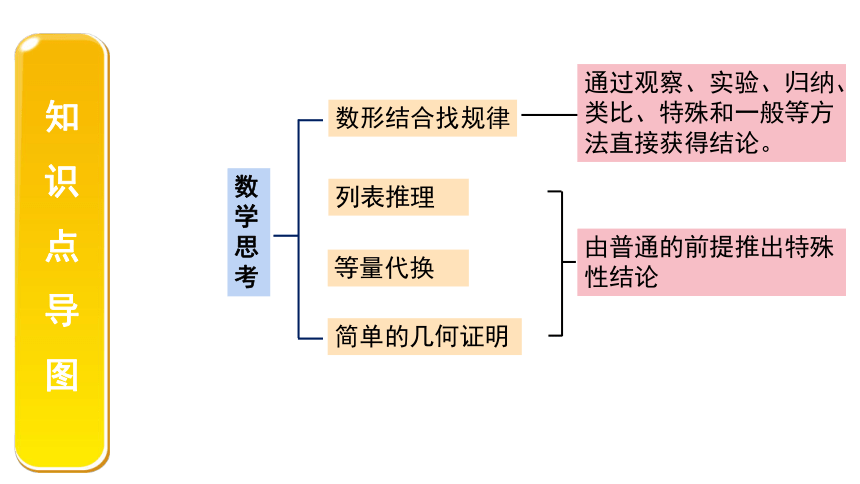
知识点导图
数学思考
数形结合找规律
列表推理
等量代换
简单的几何证明
由普通的前提推出特殊性结论
通过观察、实验、归纳、类比、特殊和一般等方法直接获得结论。
一级标题
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
在解决数学问题时常用的思想方法有哪些?
分类
比较
举例
画图
列表
符号
代入
对应
假设
转化
推理
……
回顾
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
学习《三角形》用到了分类与集合的思想
学习《小数的意义》用到了画图的方法
等腰三角形
等边三角形
三角形按边分
一般三角形
锐角三角形
直角三角形
钝角三角形
三角形按角分
回顾学过的知识用到了什么方法?
回顾
一级标题
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
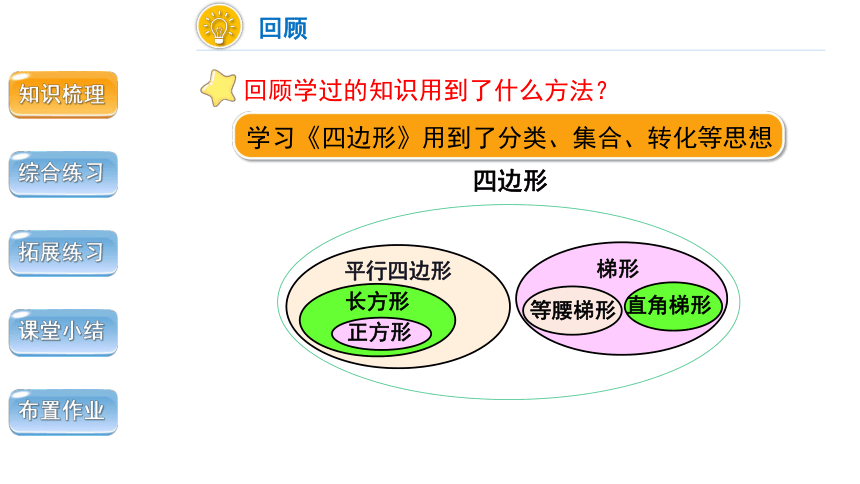
四边形
平行四边形
长方形
正方形
梯形
等腰梯形
直角梯形
学习《四边形》用到了分类、集合、转化等思想
回顾学过的知识用到了什么方法?
回顾
一级标题
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
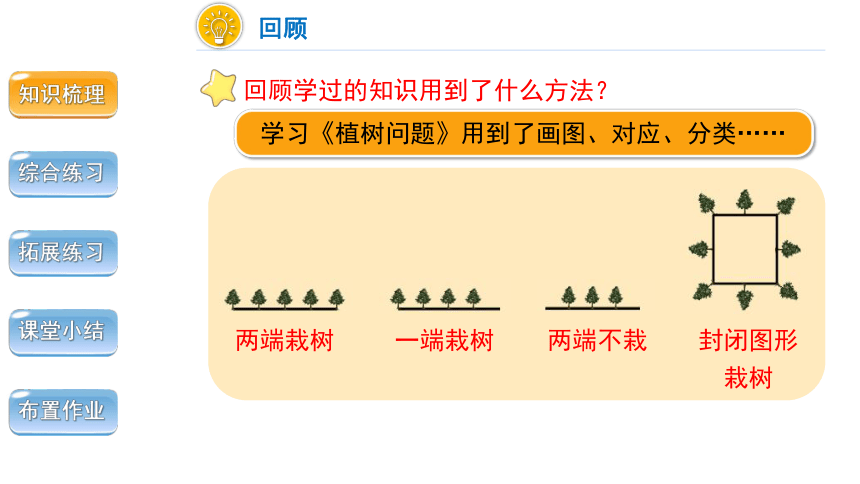
学习《植树问题》用到了画图、对应、分类……
回顾学过的知识用到了什么方法?
两端栽树
一端栽树
两端不栽
封闭图形栽树
回顾
一级标题
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
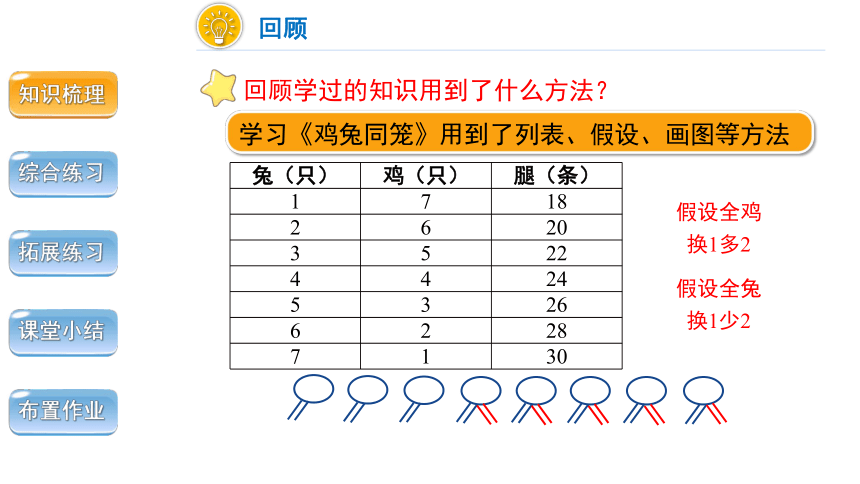
学习《鸡兔同笼》用到了列表、假设、画图等方法
兔(只) 鸡(只) 腿(条)
1 7 18
2 6 20
3 5 22
4 4 24
5 3 26
6 2 28
7 1 30
假设全鸡
换1多2
假设全兔
换1少2
回顾学过的知识用到了什么方法?
回顾
一级标题
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
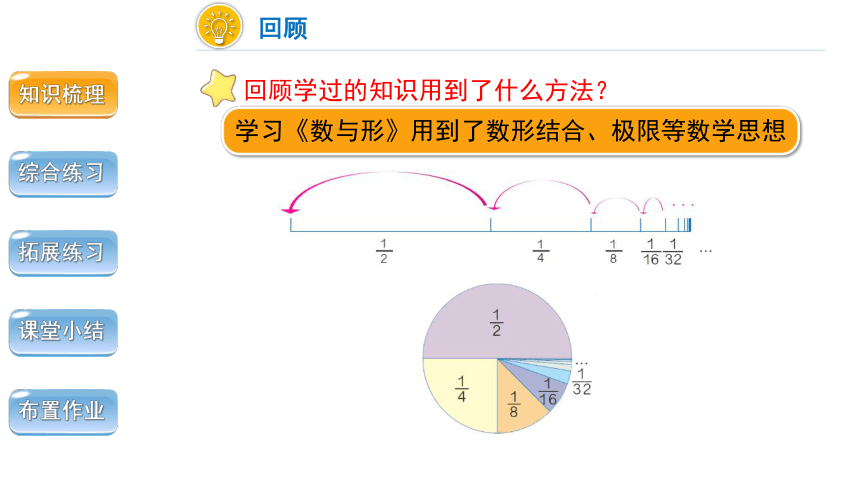
学习《数与形》用到了数形结合、极限等数学思想
回顾学过的知识用到了什么方法?
回顾
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
请你在纸上点上6个点(任意3点不能在同一条直线上)。
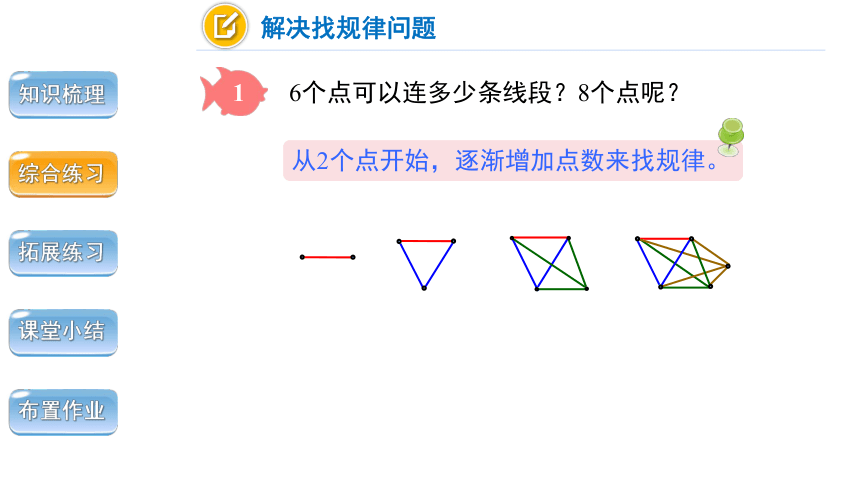
6个点可以连多少条线段?8个点呢?
1
将两点连成一条线段。
解决找规律问题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
6个点可以连多少条线段?8个点呢?
1
从2个点开始,逐渐增加点数来找规律。
解决找规律问题
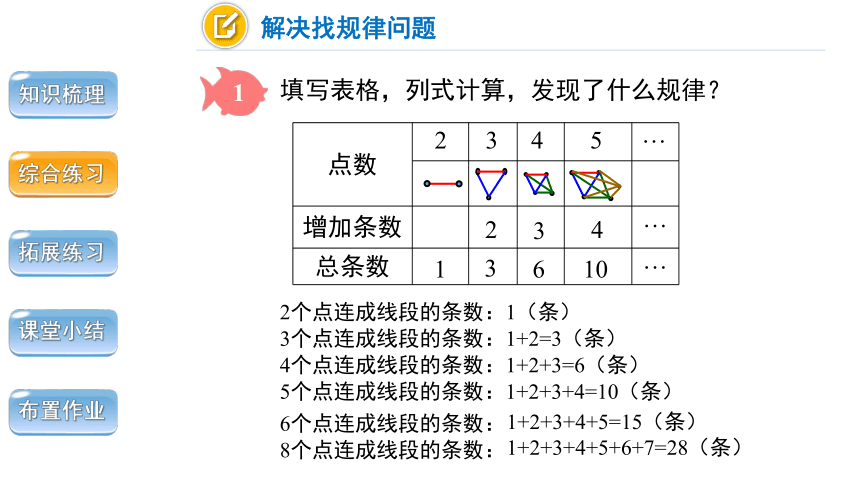
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
点数
增加条数
总条数
5个点连成线段的条数:1+2+3+4=10(条)
8个点连成线段的条数:
2
3
4
5
2
3
4
1
6
10
3
…
…
…
1+2+3+4+5=15(条)
1+2+3+4+5+6+7=28(条)
2个点连成线段的条数:1(条)
3个点连成线段的条数:1+2=3(条)
4个点连成线段的条数:1+2+3=6(条)
填写表格,列式计算,发现了什么规律?
1
6个点连成线段的条数:
解决找规律问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
1+2+3+4+5+6+7+8+9+10+11
1+2+3+4+5+6+…+18+19
101个点最多能连成多少条线段?
1+2+3+4+5+6+7+…+100
=5050(条)
1+2+3+4+5+6+7+…+(n-1)
=n(n-1)÷2(条)
=(1+100)×100÷2
12个点呢?20个点呢?请写出算式。
1
n个点最多能连成多少条线段?
解决找规律问题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
5
×
(5-1)
÷2
=10
点数×(点数-1)÷2
n(n-1)÷2
如果用n表示点数,这个规律可以表示为:
还有什么规律?
1
A
E
D
C
B
考虑到重复的线段,会得到什么结论?
遇到复杂的规律,可以化繁为简来解决,由简单情况入手,根据已知的图形或数字,探索出其中的规律。
解决找规律问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
2
用列表的方法试一试!
用数字“1”表示到会,用数字“0”表示没到会。
解决逻辑推理问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
A B C D E F
第一次
第二次
第三次
1
1
1
0
0
0
0
1
0
1
1
0
1
0
0
0
1
1
A和谁同一个班?
A B C D E F
第一次到会的情况:
A只可能和D、E或F同班
第二次到会的情况:
A只可能和D或E同班
第三次到会的情况:
A只可能和D同班
×
×
×
×
解决逻辑推理问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
×
×
第一次到会的情况:
第二次到会的情况:
B只可能和E或F同班
B只可能和F同班
A B C D E F
第一次
第二次
第三次
1
1
1
0
0
0
0
1
0
1
1
0
1
0
0
0
1
1
A B C D E F
B和谁同一个班?
剩下的C和E一定同一个班
所以,A和D同班,B和F同班,C和E同班。
解决逻辑推理问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
同时去开会的就不是同班的
你还有什么方法?
A B C D E F
第一次
第二次
第三次
√
√
√
√
√
√
√
√
√
用“√”表示到会。
第一次到会的情况:
A不可能和B、C同班
第三次到会的情况:
A不可能和E、F同班
所以A和D同班。
A B C D E F
×
×
×
×
2
解决逻辑推理问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
第一次到会的情况:
B不可能和C同班
第二次到会的情况:
B不可能和E同班
×
×
剩下的C和E一定同一个班
你还有什么方法?
A B C D E F
第一次
第二次
第三次
√
√
√
√
√
√
√
√
√
用“√”表示到会。
2
同时去开会的就不是同班的
A B C D E F
所以,A和D同班,B和F同班,C和E是同班。
解决逻辑推理问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
(1)已知△+□=24,△=□+□+□。求△的值。
可得□+□+□+□=24。
即4×□=24,所以□=6。
△=□+□+□=18。
1个△等于3个□的和。
把△+□=24中的△换成
□+□+□,这叫等量代换。
3
□
△
☆
、
、
○
、
、
◎
各代表一个数。
利用等量代换进行推理
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
已知○+☆=160,◎+☆=160,
根据等式的性质,等式两边都减去☆。
可以推出○=160-☆,◎=160-☆。
因为☆代表同一个数,所以○=◎。
等量代换与等式性质可以化难为易、化繁为简
3
□
△
☆
、
、
○
、
、
◎
各代表一个数。
两个等式里都有☆。
可以利用等式的性质。
利用等量代换进行推理
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
4
什么是平角?平角与直线有什么区别?
一条射线绕它的端点旋转半周,形成的角叫做平角。
1平角=180°
平角的两边在一条直线上。
把线段向两端无限延伸就得到一条直线。
解决简单的几何推理问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
4
如图,两条直线相交于点O。
O
1
2
3
4
(1)每相邻两个角可以组成一个平角,一共能组成几个平角?
∠1和∠2,∠2和∠3,∠3和∠4,∠4和∠1,一共能组成4个平角。
想:平角的两边在一条直线上。
(2)你能推出∠1=∠3吗?
把∠1和∠2,∠2和∠3的关系用等式表示出来。
想:∠1和∠2,∠2和∠3,都能组成平角。
解决简单的几何推理问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
根据第(1)题的结论,可以得到
∠1+∠2=180°,∠2+∠3=180°。
根据等式的性质,等式的两边都减去∠2,可以得到∠1=180°-∠2, ∠3=180°-∠2。
因为180°-∠2=180°-∠2,
所以∠1=∠3。
(2)你能推出∠1=∠3吗?
4
如图,两条直线相交于点O。
O
1
2
3
4
解决简单的几何推理问题
输入标题
课堂小结
布置作业
知识梳理
拓展练习
综合练习
1.观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
(2)第n幅图有多少个棋子?
(1)
(2)
(3)
(4)
……
答:第7幅图有49个棋子,第15幅图有225个棋子。
答:第n幅图有n2个棋子。
解决找规律问题
2.警察抓住了4个偷东西的嫌疑人,其中的一个人是主谋。审问谁是主谋时,甲说:我不是主谋。乙说:丁是主谋。丙说:我不是主谋。丁说:甲是主谋。已知他们4人中只有一个人说了真话。主谋是谁
输入标题
课堂小结
布置作业
知识梳理
拓展练习
综合练习
(2)真话确定是在甲和丁之中,就可推出乙和丙说的是假话,可知丙是主谋;
(3)那么丁说的是假话,推出甲说的是真话。
矛盾之中必有一真一假
双重否定等于肯定
(1)由于甲说的话与丁说的话互相矛盾,可推出两个人中一个说了真话,另一个说了假话;
解决逻辑推理问题
输入标题
课堂小结
布置作业
知识梳理
拓展练习
综合练习
3.○、□、△各代表一个数,根据下面的已知条件,求○、□、△的值。
(1)○+□=91 ①
△+□=63 ②
△+○=46 ③
○+□+△=100,
所以,△=9,
○=37,
□=54。
由①+②+③,得
(○+□+△)×2=200,
(2)□-○=8 ①
□+○=12 ②
△=□+□+○ ③
由①+② ,得
□×2=20,□=10,
所以,□-○=8,
○=10-8=2,
△=□+□+○,
△=10+10+2=22。
利用等量代换进行推理
输入标题
课堂小结
布置作业
知识梳理
拓展练习
综合练习
4.如图,把三角形ABC的边BC延长到点D。
(1)∠3和∠4拼成的是什么角?
(2)你能说明∠1+∠2=∠4吗?
∠3和∠4拼成的是平角。
因为∠1+∠2+∠3=180°,∠4 +∠3 =180°,
所以∠1+∠2+∠3=∠4 +∠3,
两边都减去∠3,
可以得到:∠1+∠2=∠4。
A
B
D
1
2
3
4
C
解决简单的几何推理问题
一级标题
输入标题
布置作业
知识梳理
拓展练习
课堂小结
综合练习
你有什么收获?
2.知道常用的数学思想和方法有:数形结合思想、分类思想、比较思想、假设思想、对应思想、类比思想、转化思想……
3.数学思想和方法可以帮助我们有条理地思考,简捷地解决问题。
1. 进一步掌握了找规律、列表推理、等量代换、等式性质和简单的几何证明等知识。
一级标题
输入标题
知识梳理
拓展练习
课堂小结
布置作业
综合练习
教材P103第4、5、6题
P104第7题
再见
数学思考
第六单元 整理和复习
输入标题
知识点导图
数学思考
数形结合找规律
列表推理
等量代换
简单的几何证明
由普通的前提推出特殊性结论
通过观察、实验、归纳、类比、特殊和一般等方法直接获得结论。
一级标题
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
在解决数学问题时常用的思想方法有哪些?
分类
比较
举例
画图
列表
符号
代入
对应
假设
转化
推理
……
回顾
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
学习《三角形》用到了分类与集合的思想
学习《小数的意义》用到了画图的方法
等腰三角形
等边三角形
三角形按边分
一般三角形
锐角三角形
直角三角形
钝角三角形
三角形按角分
回顾学过的知识用到了什么方法?
回顾
一级标题
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
四边形
平行四边形
长方形
正方形
梯形
等腰梯形
直角梯形
学习《四边形》用到了分类、集合、转化等思想
回顾学过的知识用到了什么方法?
回顾
一级标题
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
学习《植树问题》用到了画图、对应、分类……
回顾学过的知识用到了什么方法?
两端栽树
一端栽树
两端不栽
封闭图形栽树
回顾
一级标题
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
学习《鸡兔同笼》用到了列表、假设、画图等方法
兔(只) 鸡(只) 腿(条)
1 7 18
2 6 20
3 5 22
4 4 24
5 3 26
6 2 28
7 1 30
假设全鸡
换1多2
假设全兔
换1少2
回顾学过的知识用到了什么方法?
回顾
一级标题
输入标题
综合练习
知识梳理
拓展练习
课堂小结
布置作业
学习《数与形》用到了数形结合、极限等数学思想
回顾学过的知识用到了什么方法?
回顾
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
请你在纸上点上6个点(任意3点不能在同一条直线上)。
6个点可以连多少条线段?8个点呢?
1
将两点连成一条线段。
解决找规律问题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
6个点可以连多少条线段?8个点呢?
1
从2个点开始,逐渐增加点数来找规律。
解决找规律问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
点数
增加条数
总条数
5个点连成线段的条数:1+2+3+4=10(条)
8个点连成线段的条数:
2
3
4
5
2
3
4
1
6
10
3
…
…
…
1+2+3+4+5=15(条)
1+2+3+4+5+6+7=28(条)
2个点连成线段的条数:1(条)
3个点连成线段的条数:1+2=3(条)
4个点连成线段的条数:1+2+3=6(条)
填写表格,列式计算,发现了什么规律?
1
6个点连成线段的条数:
解决找规律问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
1+2+3+4+5+6+7+8+9+10+11
1+2+3+4+5+6+…+18+19
101个点最多能连成多少条线段?
1+2+3+4+5+6+7+…+100
=5050(条)
1+2+3+4+5+6+7+…+(n-1)
=n(n-1)÷2(条)
=(1+100)×100÷2
12个点呢?20个点呢?请写出算式。
1
n个点最多能连成多少条线段?
解决找规律问题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
5
×
(5-1)
÷2
=10
点数×(点数-1)÷2
n(n-1)÷2
如果用n表示点数,这个规律可以表示为:
还有什么规律?
1
A
E
D
C
B
考虑到重复的线段,会得到什么结论?
遇到复杂的规律,可以化繁为简来解决,由简单情况入手,根据已知的图形或数字,探索出其中的规律。
解决找规律问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
2
用列表的方法试一试!
用数字“1”表示到会,用数字“0”表示没到会。
解决逻辑推理问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
A B C D E F
第一次
第二次
第三次
1
1
1
0
0
0
0
1
0
1
1
0
1
0
0
0
1
1
A和谁同一个班?
A B C D E F
第一次到会的情况:
A只可能和D、E或F同班
第二次到会的情况:
A只可能和D或E同班
第三次到会的情况:
A只可能和D同班
×
×
×
×
解决逻辑推理问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
×
×
第一次到会的情况:
第二次到会的情况:
B只可能和E或F同班
B只可能和F同班
A B C D E F
第一次
第二次
第三次
1
1
1
0
0
0
0
1
0
1
1
0
1
0
0
0
1
1
A B C D E F
B和谁同一个班?
剩下的C和E一定同一个班
所以,A和D同班,B和F同班,C和E同班。
解决逻辑推理问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
同时去开会的就不是同班的
你还有什么方法?
A B C D E F
第一次
第二次
第三次
√
√
√
√
√
√
√
√
√
用“√”表示到会。
第一次到会的情况:
A不可能和B、C同班
第三次到会的情况:
A不可能和E、F同班
所以A和D同班。
A B C D E F
×
×
×
×
2
解决逻辑推理问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
第一次到会的情况:
B不可能和C同班
第二次到会的情况:
B不可能和E同班
×
×
剩下的C和E一定同一个班
你还有什么方法?
A B C D E F
第一次
第二次
第三次
√
√
√
√
√
√
√
√
√
用“√”表示到会。
2
同时去开会的就不是同班的
A B C D E F
所以,A和D同班,B和F同班,C和E是同班。
解决逻辑推理问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
(1)已知△+□=24,△=□+□+□。求△的值。
可得□+□+□+□=24。
即4×□=24,所以□=6。
△=□+□+□=18。
1个△等于3个□的和。
把△+□=24中的△换成
□+□+□,这叫等量代换。
3
□
△
☆
、
、
○
、
、
◎
各代表一个数。
利用等量代换进行推理
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
(2)已知○+☆=160,◎+☆=160。○是否等于◎?
已知○+☆=160,◎+☆=160,
根据等式的性质,等式两边都减去☆。
可以推出○=160-☆,◎=160-☆。
因为☆代表同一个数,所以○=◎。
等量代换与等式性质可以化难为易、化繁为简
3
□
△
☆
、
、
○
、
、
◎
各代表一个数。
两个等式里都有☆。
可以利用等式的性质。
利用等量代换进行推理
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
4
什么是平角?平角与直线有什么区别?
一条射线绕它的端点旋转半周,形成的角叫做平角。
1平角=180°
平角的两边在一条直线上。
把线段向两端无限延伸就得到一条直线。
解决简单的几何推理问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
4
如图,两条直线相交于点O。
O
1
2
3
4
(1)每相邻两个角可以组成一个平角,一共能组成几个平角?
∠1和∠2,∠2和∠3,∠3和∠4,∠4和∠1,一共能组成4个平角。
想:平角的两边在一条直线上。
(2)你能推出∠1=∠3吗?
把∠1和∠2,∠2和∠3的关系用等式表示出来。
想:∠1和∠2,∠2和∠3,都能组成平角。
解决简单的几何推理问题
输入标题
拓展练习
课堂小结
布置作业
知识梳理
综合练习
根据第(1)题的结论,可以得到
∠1+∠2=180°,∠2+∠3=180°。
根据等式的性质,等式的两边都减去∠2,可以得到∠1=180°-∠2, ∠3=180°-∠2。
因为180°-∠2=180°-∠2,
所以∠1=∠3。
(2)你能推出∠1=∠3吗?
4
如图,两条直线相交于点O。
O
1
2
3
4
解决简单的几何推理问题
输入标题
课堂小结
布置作业
知识梳理
拓展练习
综合练习
1.观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
(2)第n幅图有多少个棋子?
(1)
(2)
(3)
(4)
……
答:第7幅图有49个棋子,第15幅图有225个棋子。
答:第n幅图有n2个棋子。
解决找规律问题
2.警察抓住了4个偷东西的嫌疑人,其中的一个人是主谋。审问谁是主谋时,甲说:我不是主谋。乙说:丁是主谋。丙说:我不是主谋。丁说:甲是主谋。已知他们4人中只有一个人说了真话。主谋是谁
输入标题
课堂小结
布置作业
知识梳理
拓展练习
综合练习
(2)真话确定是在甲和丁之中,就可推出乙和丙说的是假话,可知丙是主谋;
(3)那么丁说的是假话,推出甲说的是真话。
矛盾之中必有一真一假
双重否定等于肯定
(1)由于甲说的话与丁说的话互相矛盾,可推出两个人中一个说了真话,另一个说了假话;
解决逻辑推理问题
输入标题
课堂小结
布置作业
知识梳理
拓展练习
综合练习
3.○、□、△各代表一个数,根据下面的已知条件,求○、□、△的值。
(1)○+□=91 ①
△+□=63 ②
△+○=46 ③
○+□+△=100,
所以,△=9,
○=37,
□=54。
由①+②+③,得
(○+□+△)×2=200,
(2)□-○=8 ①
□+○=12 ②
△=□+□+○ ③
由①+② ,得
□×2=20,□=10,
所以,□-○=8,
○=10-8=2,
△=□+□+○,
△=10+10+2=22。
利用等量代换进行推理
输入标题
课堂小结
布置作业
知识梳理
拓展练习
综合练习
4.如图,把三角形ABC的边BC延长到点D。
(1)∠3和∠4拼成的是什么角?
(2)你能说明∠1+∠2=∠4吗?
∠3和∠4拼成的是平角。
因为∠1+∠2+∠3=180°,∠4 +∠3 =180°,
所以∠1+∠2+∠3=∠4 +∠3,
两边都减去∠3,
可以得到:∠1+∠2=∠4。
A
B
D
1
2
3
4
C
解决简单的几何推理问题
一级标题
输入标题
布置作业
知识梳理
拓展练习
课堂小结
综合练习
你有什么收获?
2.知道常用的数学思想和方法有:数形结合思想、分类思想、比较思想、假设思想、对应思想、类比思想、转化思想……
3.数学思想和方法可以帮助我们有条理地思考,简捷地解决问题。
1. 进一步掌握了找规律、列表推理、等量代换、等式性质和简单的几何证明等知识。
一级标题
输入标题
知识梳理
拓展练习
课堂小结
布置作业
综合练习
教材P103第4、5、6题
P104第7题
再见
