5.2.2 平行线的判定 巩固练习(含答案)2022--2023学年人教版七年级数学下册
文档属性
| 名称 | 5.2.2 平行线的判定 巩固练习(含答案)2022--2023学年人教版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 152.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-17 00:00:00 | ||
图片预览



文档简介
5.2.2 平行线的判定 巩固练习
一、单选题
1.如图,在下列给出的条件下,不能判定AB∥DF的是( )
A.∠A+∠2=180° B.∠A=∠3
C.∠1=∠4 D.∠1=∠A
2.如图,下列条件中能判断直线 AD∥BC 的是( )
A.∠A=∠ABC B.∠ADB=∠CBD
C.∠A+∠ADC=180° D.∠A=∠C
3.同一平面内的四条直线,若满足a⊥b, b⊥c, c⊥d,则下列的式子成立的是 ( )
A.a//d B.b⊥d C.a⊥d D.b//c
4.下列说法正确的个数是.( )
(1)过直线外一点有且只有一条直线与已知直线平行.
(2)在同一个平面内,过一点有且只有一条直线与已知直线垂直.
(3)内错角相等
(4)平行于同一条直线的两直线平行
(5)同位角相等,两直线平行
A.2 B.3 C.4 D.5
5.如图,已知∠2=110°,要使a∥b,则须具备另一个条件( )
A.∠3=70° B.∠3=110° C.∠4=70° D.∠1=70°
6.如图,下列推理错误的是( )
A.∵∠1=∠3∴a∥b B.∵∠1=∠2∴a∥b
C.∵∠3=∠5∴c∥d D.∵∠2+∠4=180°∴c∥d
7.在△ABC中,点D与点E分别在边AB、AC上,下列比例式能判断DE∥BC的是( )
A.DE:BC=AD:BD B.DE:BC=AB:AD
C.AD:AE=AC:AB D.DB:EC=AB:AC
8.将如图中的说理过程补充完整.下列补充错误的是( )
如图,,直线与,分别相交于点,,平分,平分,对说明理由. 解:(已知), ∴①=∠CNE(两直线平行,同位角相等) 平分,平分已知, ,(②) (③),.
A.①表示
B.②表示角平分线的定义
C.③表示等量代换
D.④表示内错角相等,两直线平行
9.下列命题是假命题的( )
A.在同一平面内,若a∥b,b∥c,则a∥c
B.在同一平面内,若a⊥b,b∥c,则a⊥c
C.在同一平面内,若a⊥b,b⊥c,则a⊥c
D.在同一平面内,若a⊥b,b⊥c,则a∥c
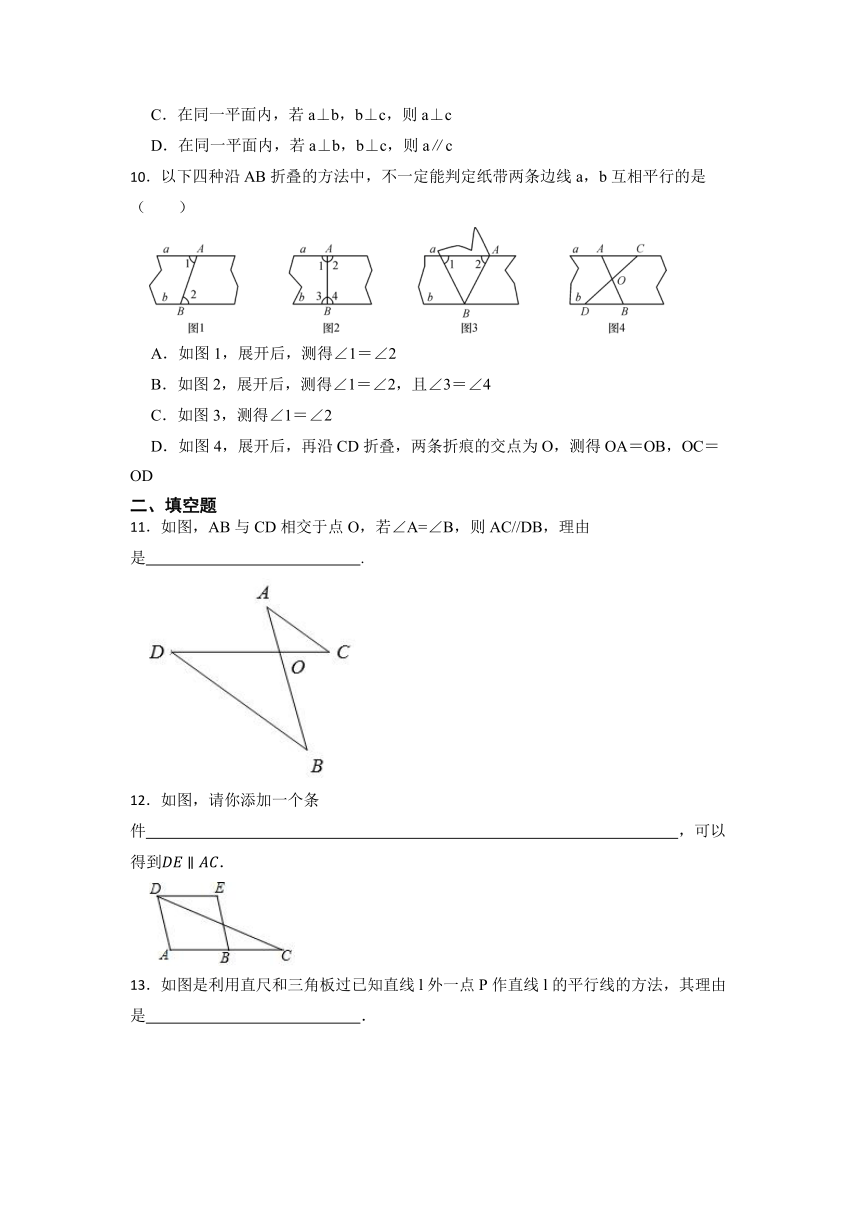
10.以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
A.如图1,展开后,测得∠1=∠2
B.如图2,展开后,测得∠1=∠2,且∠3=∠4
C.如图3,测得∠1=∠2
D.如图4,展开后,再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
二、填空题
11.如图,AB与CD相交于点O,若∠A=∠B,则AC//DB,理由是 .
12.如图,请你添加一个条
件 ,可以得到.
13.如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是 .
14.如图,写出能判定AB∥CD的一对角的数量关系: .
15.如图,过直线外一点D画已知直线AB的平行线.首先画直线AB,将三角尺的一边紧靠直线AB,将直尺紧靠三角尺的另一边;然后将三角尺沿直尺下移;最后当三角尺原紧靠直线AB的那一边经过点D时,画直线CD.这样就得到CD∥AB.这种画法的依据是 .
三、解答题
16.如图AB,CD为⊙O内两条相交的弦,交点为E,且AB=CD,求证:AD∥BC.
17.如图,已知,,.求证:.请你完成下列填空,把证明过程补充完整
证明:∵ ▲ , ▲
∴,( ),
∴,.
又∵,
∴( ),
∴( ).
18.如图所示,已知∠1是它的补角的3倍,∠2等于它的余角,那么AB//CD吗?为什么?
19.如图, 中, 是 的平分线, 交 于 , , ,求 的度数.
20.如图,已知∠1=∠2,AD=2BC,三角形ABC的面积为3,求△CAD的面积。
参考答案
1.D
2.B
3.C
4.C
5.A
6.A
7.D
8.D
9.C
10.C
11.内错角相等,两直线平行
12.答案不唯一,当添加条件∠EDC=∠C或∠E=∠EBC或∠E+∠EBA=180°或∠A+∠ADE=180°时,都可以得到DEAC.
13.同位角相等,两直线平行
14.∠BAC=∠ACD(或∠B+∠BCD=180°或∠D+∠BAD=180°)
15.同位角相等两直线平行
16.证明:∵AB=CD,
∴ =,
∴﹣=﹣,
即=,
∴∠A=∠B,
∴AD∥BC.
17.证明:∵,,
∴,(垂直的定义)
∴,,
又∵
∴(等角的余角相等),
∴(内错角相等,两直线平行).
18.解:AB∥CD.理由如下:
∵∠1=3(180°-∠1),∴∠1= 135°.
∵∠2=90°-∠2.∴∠2=45°,
∴∠1+∠2=135°+45°= 180°,
∴AB∥CD(同旁内角互补,两直线平行).
19.∵ , ,
∴ .
在 中, ,
∴ .
∵ 是 的平分线,
∴ .
∴
20.解:∵ ∠1=∠2,
∴ AD∥BC,
∴ △CAD和△ABC的高相等,
∵ AD=2BC,
∴S△CAD=2S△ABC=2×3=6.
一、单选题
1.如图,在下列给出的条件下,不能判定AB∥DF的是( )
A.∠A+∠2=180° B.∠A=∠3
C.∠1=∠4 D.∠1=∠A
2.如图,下列条件中能判断直线 AD∥BC 的是( )
A.∠A=∠ABC B.∠ADB=∠CBD
C.∠A+∠ADC=180° D.∠A=∠C
3.同一平面内的四条直线,若满足a⊥b, b⊥c, c⊥d,则下列的式子成立的是 ( )
A.a//d B.b⊥d C.a⊥d D.b//c
4.下列说法正确的个数是.( )
(1)过直线外一点有且只有一条直线与已知直线平行.
(2)在同一个平面内,过一点有且只有一条直线与已知直线垂直.
(3)内错角相等
(4)平行于同一条直线的两直线平行
(5)同位角相等,两直线平行
A.2 B.3 C.4 D.5
5.如图,已知∠2=110°,要使a∥b,则须具备另一个条件( )
A.∠3=70° B.∠3=110° C.∠4=70° D.∠1=70°
6.如图,下列推理错误的是( )
A.∵∠1=∠3∴a∥b B.∵∠1=∠2∴a∥b
C.∵∠3=∠5∴c∥d D.∵∠2+∠4=180°∴c∥d
7.在△ABC中,点D与点E分别在边AB、AC上,下列比例式能判断DE∥BC的是( )
A.DE:BC=AD:BD B.DE:BC=AB:AD
C.AD:AE=AC:AB D.DB:EC=AB:AC
8.将如图中的说理过程补充完整.下列补充错误的是( )
如图,,直线与,分别相交于点,,平分,平分,对说明理由. 解:(已知), ∴①=∠CNE(两直线平行,同位角相等) 平分,平分已知, ,(②) (③),.
A.①表示
B.②表示角平分线的定义
C.③表示等量代换
D.④表示内错角相等,两直线平行
9.下列命题是假命题的( )
A.在同一平面内,若a∥b,b∥c,则a∥c
B.在同一平面内,若a⊥b,b∥c,则a⊥c
C.在同一平面内,若a⊥b,b⊥c,则a⊥c
D.在同一平面内,若a⊥b,b⊥c,则a∥c
10.以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
A.如图1,展开后,测得∠1=∠2
B.如图2,展开后,测得∠1=∠2,且∠3=∠4
C.如图3,测得∠1=∠2
D.如图4,展开后,再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
二、填空题
11.如图,AB与CD相交于点O,若∠A=∠B,则AC//DB,理由是 .
12.如图,请你添加一个条
件 ,可以得到.
13.如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是 .
14.如图,写出能判定AB∥CD的一对角的数量关系: .
15.如图,过直线外一点D画已知直线AB的平行线.首先画直线AB,将三角尺的一边紧靠直线AB,将直尺紧靠三角尺的另一边;然后将三角尺沿直尺下移;最后当三角尺原紧靠直线AB的那一边经过点D时,画直线CD.这样就得到CD∥AB.这种画法的依据是 .
三、解答题
16.如图AB,CD为⊙O内两条相交的弦,交点为E,且AB=CD,求证:AD∥BC.
17.如图,已知,,.求证:.请你完成下列填空,把证明过程补充完整
证明:∵ ▲ , ▲
∴,( ),
∴,.
又∵,
∴( ),
∴( ).
18.如图所示,已知∠1是它的补角的3倍,∠2等于它的余角,那么AB//CD吗?为什么?
19.如图, 中, 是 的平分线, 交 于 , , ,求 的度数.
20.如图,已知∠1=∠2,AD=2BC,三角形ABC的面积为3,求△CAD的面积。
参考答案
1.D
2.B
3.C
4.C
5.A
6.A
7.D
8.D
9.C
10.C
11.内错角相等,两直线平行
12.答案不唯一,当添加条件∠EDC=∠C或∠E=∠EBC或∠E+∠EBA=180°或∠A+∠ADE=180°时,都可以得到DEAC.
13.同位角相等,两直线平行
14.∠BAC=∠ACD(或∠B+∠BCD=180°或∠D+∠BAD=180°)
15.同位角相等两直线平行
16.证明:∵AB=CD,
∴ =,
∴﹣=﹣,
即=,
∴∠A=∠B,
∴AD∥BC.
17.证明:∵,,
∴,(垂直的定义)
∴,,
又∵
∴(等角的余角相等),
∴(内错角相等,两直线平行).
18.解:AB∥CD.理由如下:
∵∠1=3(180°-∠1),∴∠1= 135°.
∵∠2=90°-∠2.∴∠2=45°,
∴∠1+∠2=135°+45°= 180°,
∴AB∥CD(同旁内角互补,两直线平行).
19.∵ , ,
∴ .
在 中, ,
∴ .
∵ 是 的平分线,
∴ .
∴
20.解:∵ ∠1=∠2,
∴ AD∥BC,
∴ △CAD和△ABC的高相等,
∵ AD=2BC,
∴S△CAD=2S△ABC=2×3=6.
