第六章 概率初步 达标检测 含答案 2022—2023学年北师大版数学七年级下册
文档属性
| 名称 | 第六章 概率初步 达标检测 含答案 2022—2023学年北师大版数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 347.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-18 07:36:54 | ||
图片预览


文档简介
七下-第六章 概率初步 达标检测
一、选择题(共12小题)
1. 下列事件中,是必然事件的是
A. 打开电视机,正在播放新闻
B. 父亲年龄比儿子年龄大
C. 通过长期努力学习,你会成为数学家
D. 下雨天,每个人都打着雨伞
2. 用扇形统计图反映地球上陆地面积与海洋面积所占比例时,陆地面积所对应的圆心角是 ,当宇宙中一块陨石落在地球上,则落在陆地上的概率是
A. B. C. D.
3. 下列说法正确的是
A. “明天的降水概率为 ”是指明天下雨的可能性是
B. 连续抛一枚硬币 次,出现正面朝上的次数一定是 次
C. 连续三次掷一颗骰子都出现了奇数,则第四次出现的数一定是偶数
D. 某地发行一种福利彩票,中奖概率为 ,买这种彩票 张一定会中奖
4. 四张卡片分别标有数学 ,,,,任意抽出一张,数字是偶数的概率为
A. B. C. D.
5. 小狗在如图所示的方砖上走来走去,最终停在黑色方砖上的概率为
A. B. C. D.
6. 小刚掷一枚硬币,一连 次都掷出正面朝上,当他再一次掷硬币时,出现正面朝上的概率是
A. B. C. D.
7. 为备战考试,同学们积极投入复习,李红书包里装有语文试卷 张、数学试卷 张、英语试卷 张、其他学科试卷 张,从中任意抽出一张试卷,恰好是数学试卷的概率是
A. B. C. D.
8. 从长度分别为 ,,, 的四条线段中任选三条作边,能构成三角形的概率为
A. B. C. D.
9. 小明和小亮做游戏,先是各自背着对方在纸上写一个正整数,然后都拿给对方看.他们约定,若两人所写的数都是奇数或都是偶数,则小明获胜;若两个人所写的数一个是奇数,另一个是偶数,则小亏获胜.这个游戏
A. 对小明有利 B. 对小亮有利
C. 公平 D. 无法确定对谁有利
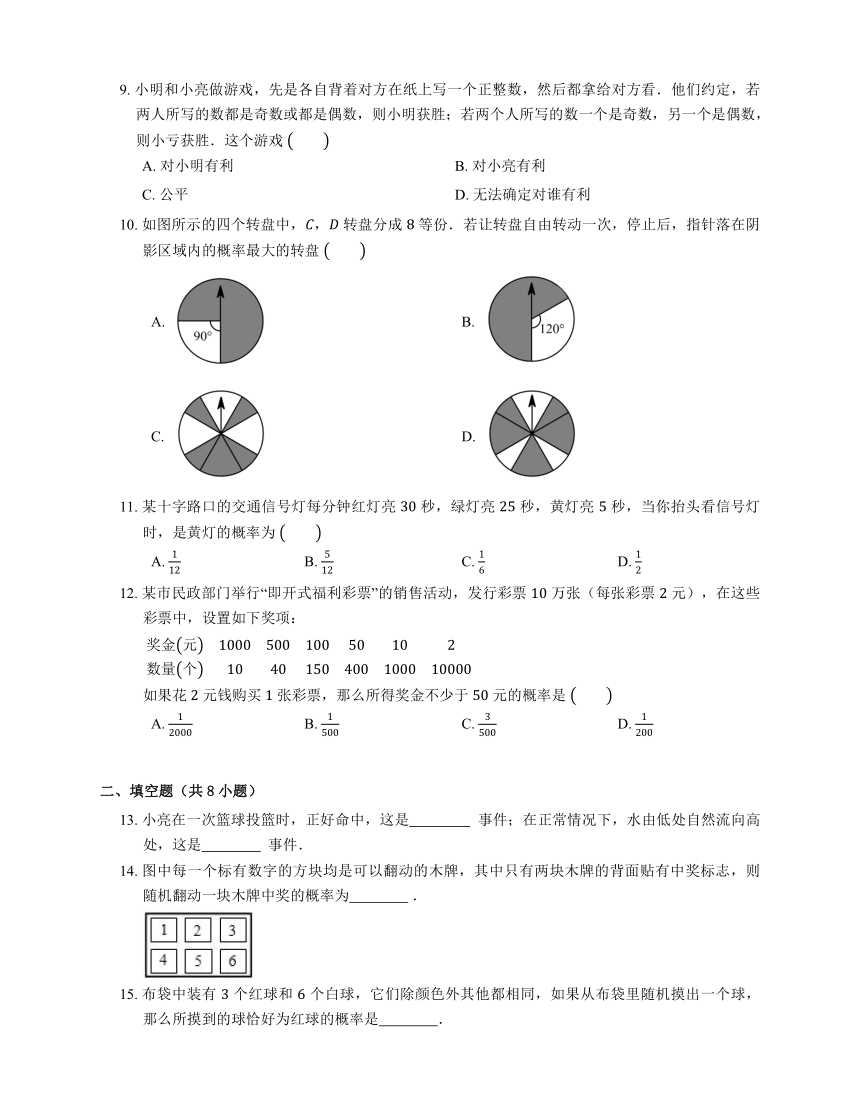
10. 如图所示的四个转盘中,, 转盘分成 等份.若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘
A. B.
C. D.
11. 某十字路口的交通信号灯每分钟红灯亮 秒,绿灯亮 秒,黄灯亮 秒,当你抬头看信号灯时,是黄灯的概率为
A. B. C. D.
12. 某市民政部门举行“即开式福利彩票”的销售活动,发行彩票 万张(每张彩票 元),在这些彩票中,设置如下奖项:
如果花 元钱购买 张彩票,那么所得奖金不少于 元的概率是
A. B. C. D.
二、填空题(共8小题)
13. 小亮在一次篮球投篮时,正好命中,这是 事件;在正常情况下,水由低处自然流向高处,这是 事件.
14. 图中每一个标有数字的方块均是可以翻动的木牌,其中只有两块木牌的背面贴有中奖标志,则随机翻动一块木牌中奖的概率为 .
15. 布袋中装有 个红球和 个白球,它们除颜色外其他都相同,如果从布袋里随机摸出一个球,那么所摸到的球恰好为红球的概率是 .
16. 有四张质地、大小、反面完全相同的不透明卡片,正面分别写着数字 ,,,,现把它们的正面向下,随机摆放在桌面上,从中任意抽出一张,则抽出的数字是奇数的概率是 .
17. 如图所示是一个被等分成 个扇形且可自由转动的转盘,转动转盘,当转盘停止后,指针指向红色区域的概率 .
18. 在数字 ,, 中任选两个组成一个两位数,则这个两位数能被 整除的概率是 .
19. 有大、小两个同心圆,它们的半径分别是 和 .随机掷一枚飞镖,飞镖钉在小圆中的概率是 .
20. 一个暗箱里放有 个除颜色外完全相同的球,这 个球中红球只有 个.若每次将球搅匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球试验后发现,摸到红球的频率稳定在 附近,那么可以推算出 的值大约是 .
三、解答题(共4小题)
21. 请将下列事件发生的概率标在下图中(标序号).
(1)十五的月亮就像一个弯弯细钩;
(2)正常情况下,气温低于零摄氏度,水会结冰;
(3)任意掷一枚六面分别写有 ,,,,, 的均匀骰子,标有数字 的一面朝上;
(4)从装有 个红球、 个白球、 个黄球的口袋中任取一个球,恰好是白球(这些球除颜色外完全相同).
22. 如图所示是芳芳设计的自由转动的转盘,上面写有 个数字,求转得下列各数的概率:
(1)转得正数;
(2)转得正整数;
(3)转得绝对值小于 的数;
(4)转得绝对值小于等于 的数.
23. 某商场设立了一个可以自由转动的转盘,并规定:顾客购物 元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据:
(1)计算并完成表格;
(2)请估计,当 很大时,频率将会接近多少
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少 (精确到 )
24. 在一只不透明的袋子中,装有 个白球和 个红球,这些球除颜色外都相同.
(1)小明认为,搅匀后从中任意摸出一个球,不是白球就是红球,因此摸出白球和摸出红球是等可能的.你同意他的说法吗 为什么
(2)搅匀后从中一把摸出两个球,请通过列举各种情况,求出两个球都是白球的概率.
(3)搅匀后从中任意摸出一个球,要使摸出红球的概率为 ,应如何添加红球
答案
1. B
2. B
【解析】根据“陆地”部分的圆心角占整个圆心角的比求出落在陆地上的概率.因为 ,所以宇宙中一块陨石落在陆地上的概率是 .
3. A
4. B
5. C
6. C
7. D
8. C
9. C
10. A
11. A
【解析】随机事件 的概率 ,
据此用黄灯亮的时间除以三种灯亮的总时间,可求出抬头看信号灯时,是黄灯的概率为 .
12. C
13. 不确定,不可能
14.
15.
16.
17.
18.
19.
20.
21. (1)
(2)
(3)
(4)
22. (1) 正数有 个数字
概率为 .
(2) 正整数有 个数字
概率为 .
(3) 绝对值小于 的数有 个数字.
概率为 .
(4) 绝对值小于等于 的数有 个数字.
概率为 .
23. (1)
(2) 当 很大时,频率将会接近 .
(3) 获得铅笔的概率约是 .
(4) 扇形的圆心角的度数为 .
24. (1) 不同意,因为白球跟红球的个数不同.
(2) 共有 种情况:(白 ,白 ),(白 ,红),(,红),其中两个都是白球的有 种,所以两个球都是白球的概率为 .
(3) 设添加红球 个,
可得 .
解得 .
添加 个红球.
一、选择题(共12小题)
1. 下列事件中,是必然事件的是
A. 打开电视机,正在播放新闻
B. 父亲年龄比儿子年龄大
C. 通过长期努力学习,你会成为数学家
D. 下雨天,每个人都打着雨伞
2. 用扇形统计图反映地球上陆地面积与海洋面积所占比例时,陆地面积所对应的圆心角是 ,当宇宙中一块陨石落在地球上,则落在陆地上的概率是
A. B. C. D.
3. 下列说法正确的是
A. “明天的降水概率为 ”是指明天下雨的可能性是
B. 连续抛一枚硬币 次,出现正面朝上的次数一定是 次
C. 连续三次掷一颗骰子都出现了奇数,则第四次出现的数一定是偶数
D. 某地发行一种福利彩票,中奖概率为 ,买这种彩票 张一定会中奖
4. 四张卡片分别标有数学 ,,,,任意抽出一张,数字是偶数的概率为
A. B. C. D.
5. 小狗在如图所示的方砖上走来走去,最终停在黑色方砖上的概率为
A. B. C. D.
6. 小刚掷一枚硬币,一连 次都掷出正面朝上,当他再一次掷硬币时,出现正面朝上的概率是
A. B. C. D.
7. 为备战考试,同学们积极投入复习,李红书包里装有语文试卷 张、数学试卷 张、英语试卷 张、其他学科试卷 张,从中任意抽出一张试卷,恰好是数学试卷的概率是
A. B. C. D.
8. 从长度分别为 ,,, 的四条线段中任选三条作边,能构成三角形的概率为
A. B. C. D.
9. 小明和小亮做游戏,先是各自背着对方在纸上写一个正整数,然后都拿给对方看.他们约定,若两人所写的数都是奇数或都是偶数,则小明获胜;若两个人所写的数一个是奇数,另一个是偶数,则小亏获胜.这个游戏
A. 对小明有利 B. 对小亮有利
C. 公平 D. 无法确定对谁有利
10. 如图所示的四个转盘中,, 转盘分成 等份.若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘
A. B.
C. D.
11. 某十字路口的交通信号灯每分钟红灯亮 秒,绿灯亮 秒,黄灯亮 秒,当你抬头看信号灯时,是黄灯的概率为
A. B. C. D.
12. 某市民政部门举行“即开式福利彩票”的销售活动,发行彩票 万张(每张彩票 元),在这些彩票中,设置如下奖项:
如果花 元钱购买 张彩票,那么所得奖金不少于 元的概率是
A. B. C. D.
二、填空题(共8小题)
13. 小亮在一次篮球投篮时,正好命中,这是 事件;在正常情况下,水由低处自然流向高处,这是 事件.
14. 图中每一个标有数字的方块均是可以翻动的木牌,其中只有两块木牌的背面贴有中奖标志,则随机翻动一块木牌中奖的概率为 .
15. 布袋中装有 个红球和 个白球,它们除颜色外其他都相同,如果从布袋里随机摸出一个球,那么所摸到的球恰好为红球的概率是 .
16. 有四张质地、大小、反面完全相同的不透明卡片,正面分别写着数字 ,,,,现把它们的正面向下,随机摆放在桌面上,从中任意抽出一张,则抽出的数字是奇数的概率是 .
17. 如图所示是一个被等分成 个扇形且可自由转动的转盘,转动转盘,当转盘停止后,指针指向红色区域的概率 .
18. 在数字 ,, 中任选两个组成一个两位数,则这个两位数能被 整除的概率是 .
19. 有大、小两个同心圆,它们的半径分别是 和 .随机掷一枚飞镖,飞镖钉在小圆中的概率是 .
20. 一个暗箱里放有 个除颜色外完全相同的球,这 个球中红球只有 个.若每次将球搅匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球试验后发现,摸到红球的频率稳定在 附近,那么可以推算出 的值大约是 .
三、解答题(共4小题)
21. 请将下列事件发生的概率标在下图中(标序号).
(1)十五的月亮就像一个弯弯细钩;
(2)正常情况下,气温低于零摄氏度,水会结冰;
(3)任意掷一枚六面分别写有 ,,,,, 的均匀骰子,标有数字 的一面朝上;
(4)从装有 个红球、 个白球、 个黄球的口袋中任取一个球,恰好是白球(这些球除颜色外完全相同).
22. 如图所示是芳芳设计的自由转动的转盘,上面写有 个数字,求转得下列各数的概率:
(1)转得正数;
(2)转得正整数;
(3)转得绝对值小于 的数;
(4)转得绝对值小于等于 的数.
23. 某商场设立了一个可以自由转动的转盘,并规定:顾客购物 元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据:
(1)计算并完成表格;
(2)请估计,当 很大时,频率将会接近多少
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少 (精确到 )
24. 在一只不透明的袋子中,装有 个白球和 个红球,这些球除颜色外都相同.
(1)小明认为,搅匀后从中任意摸出一个球,不是白球就是红球,因此摸出白球和摸出红球是等可能的.你同意他的说法吗 为什么
(2)搅匀后从中一把摸出两个球,请通过列举各种情况,求出两个球都是白球的概率.
(3)搅匀后从中任意摸出一个球,要使摸出红球的概率为 ,应如何添加红球
答案
1. B
2. B
【解析】根据“陆地”部分的圆心角占整个圆心角的比求出落在陆地上的概率.因为 ,所以宇宙中一块陨石落在陆地上的概率是 .
3. A
4. B
5. C
6. C
7. D
8. C
9. C
10. A
11. A
【解析】随机事件 的概率 ,
据此用黄灯亮的时间除以三种灯亮的总时间,可求出抬头看信号灯时,是黄灯的概率为 .
12. C
13. 不确定,不可能
14.
15.
16.
17.
18.
19.
20.
21. (1)
(2)
(3)
(4)
22. (1) 正数有 个数字
概率为 .
(2) 正整数有 个数字
概率为 .
(3) 绝对值小于 的数有 个数字.
概率为 .
(4) 绝对值小于等于 的数有 个数字.
概率为 .
23. (1)
(2) 当 很大时,频率将会接近 .
(3) 获得铅笔的概率约是 .
(4) 扇形的圆心角的度数为 .
24. (1) 不同意,因为白球跟红球的个数不同.
(2) 共有 种情况:(白 ,白 ),(白 ,红),(,红),其中两个都是白球的有 种,所以两个球都是白球的概率为 .
(3) 设添加红球 个,
可得 .
解得 .
添加 个红球.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
