第三章 圆 章末测试卷 含答案 2022—2023学年北师大版数学九年级下册
文档属性
| 名称 | 第三章 圆 章末测试卷 含答案 2022—2023学年北师大版数学九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-18 07:44:56 | ||
图片预览


文档简介
九下-第三章 圆 章末测试卷
一、选择题(共10小题)
1. 是 外一点,, 分别交 于 , 两点,已知 , 的度数分别为 ,,则 的度数为
A. B. C. D.
2. 下列说法正确的是
A. 三点确定一个圆
B. 一个三角形只有一个外接圆
C. 和半径垂直的直线是圆的切线
D. 三角形的内心到三角形三个顶点距离相等
3. 如图, 是圆 的直径,,, 是圆 的弦,且 ,则 等于
A. B. C. D.
4. 已知 的半径为 ,圆心到点 的距离为 ,且 , 分别是方程 的两根,则点 与 的位置关系是
A. 点 在 内部 B. 点 在 上
C. 点 在 外部 D. 点 不在 上
5. 在 中,,,, 的内心与顶点 的距离为
A. B. C. D.
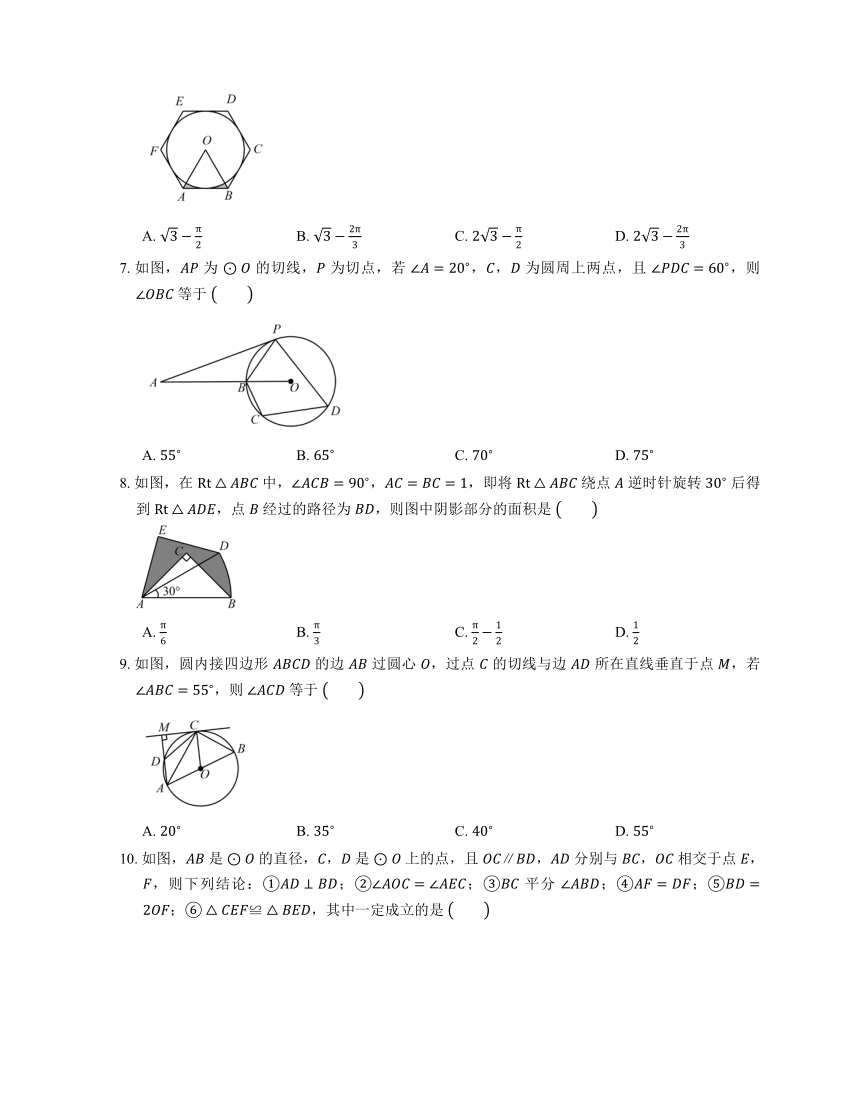
6. 如图, 的外切正六边形 的边长为 ,则图中阴影部分的面积为
A. B. C. D.
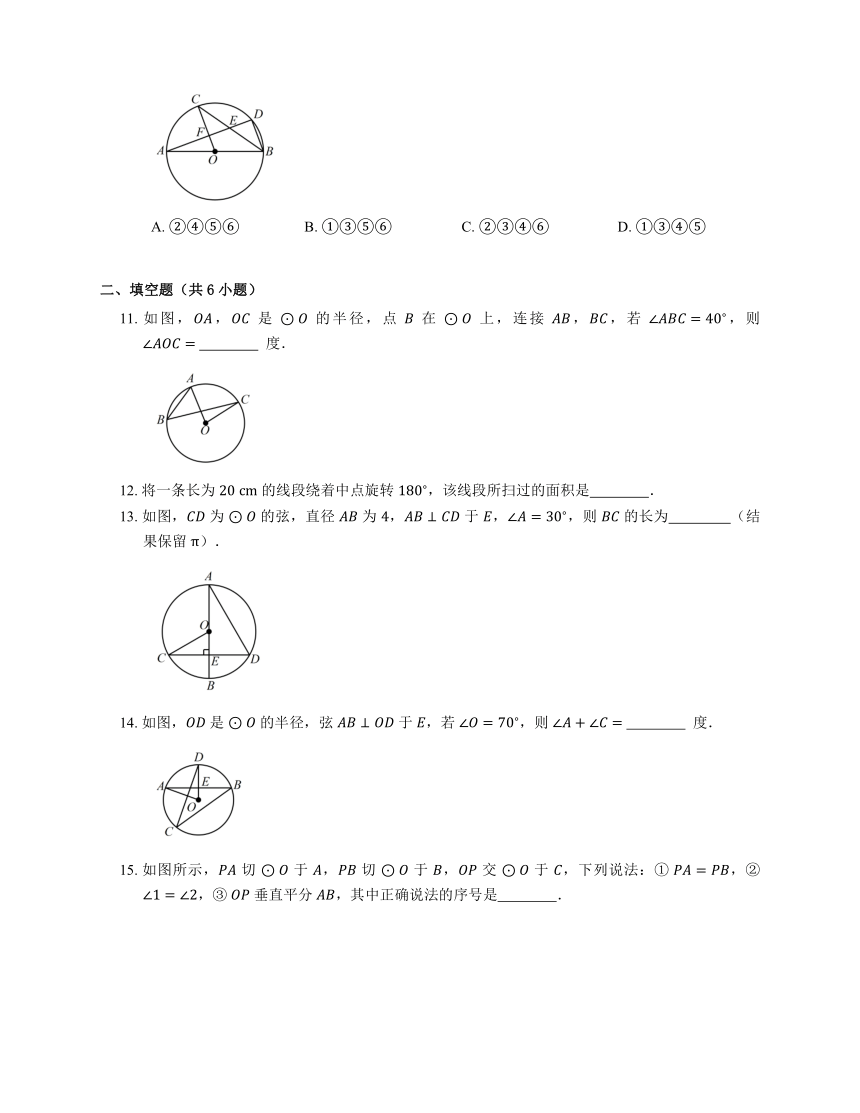
7. 如图, 为 的切线, 为切点,若 ,, 为圆周上两点,且 ,则 等于
A. B. C. D.
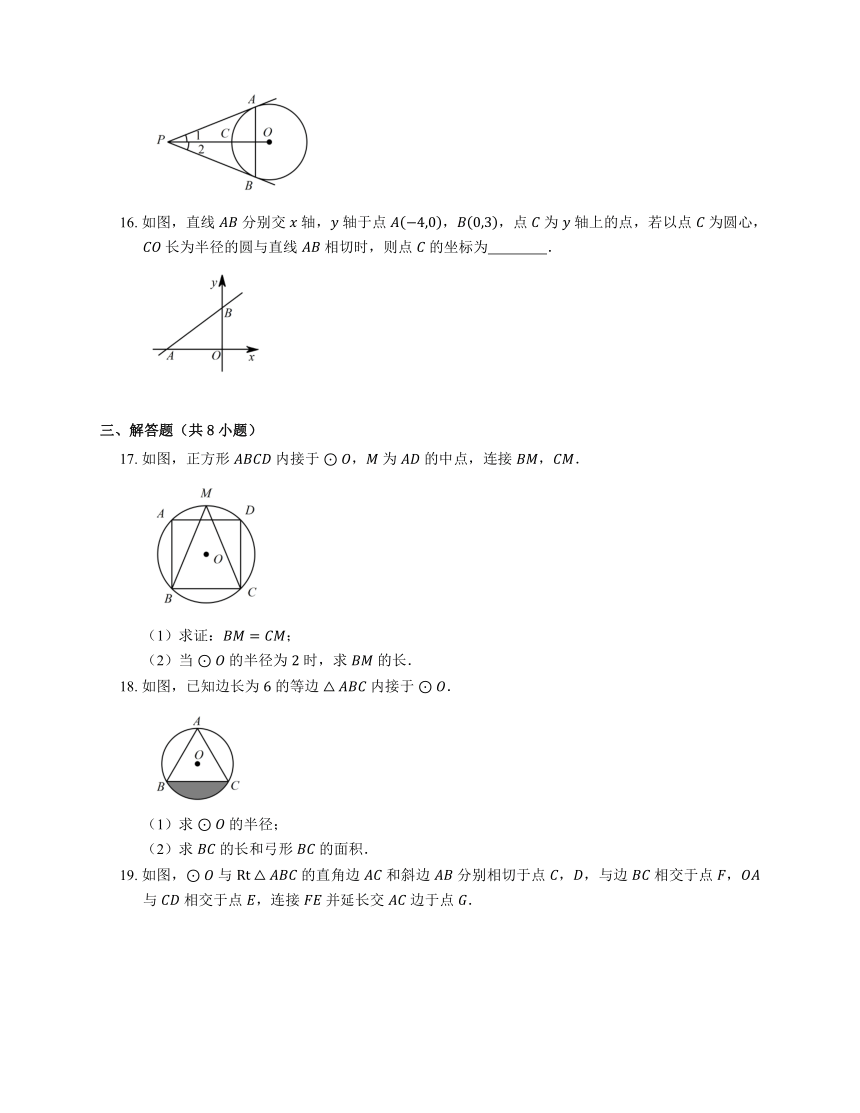
8. 如图,在 中,,,即将 绕点 逆时针旋转 后得到 ,点 经过的路径为 ,则图中阴影部分的面积是
A. B. C. D.
9. 如图,圆内接四边形 的边 过圆心 ,过点 的切线与边 所在直线垂直于点 ,若 ,则 等于
A. B. C. D.
10. 如图, 是 的直径,, 是 上的点,且 , 分别与 , 相交于点 ,,则下列结论:;; 平分 ;;;,其中一定成立的是
A. B. C. D.
二、填空题(共6小题)
11. 如图,, 是 的半径,点 在 上,连接 ,,若 ,则 度.
12. 将一条长为 的线段绕着中点旋转 ,该线段所扫过的面积是 .
13. 如图, 为 的弦,直径 为 , 于 ,,则 的长为 (结果保留 ).
14. 如图, 是 的半径,弦 于 ,若 ,则 度.
15. 如图所示, 切 于 , 切 于 , 交 于 ,下列说法:① ,② ,③ 垂直平分 ,其中正确说法的序号是 .
16. 如图,直线 分别交 轴, 轴于点 ,,点 为 轴上的点,若以点 为圆心, 长为半径的圆与直线 相切时,则点 的坐标为 .
三、解答题(共8小题)
17. 如图,正方形 内接于 , 为 的中点,连接 ,.
(1)求证:;
(2)当 的半径为 时,求 的长.
18. 如图,已知边长为 的等边 内接于 .
(1)求 的半径;
(2)求 的长和弓形 的面积.
19. 如图, 与 的直角边 和斜边 分别相切于点 ,,与边 相交于点 , 与 相交于点 ,连接 并延长交 边于点 .
(1)求证:;
(2)若 ,,求 的长.
20. 如图,在 中,,以 为直径作 交 于点 , 为 的中点,连接 并延长交 的延长线于点 .
(1)求证: 是 的切线;
(2)若 ,,求 直径的长.
21. 如图, 是 的直径,线段 过圆心 ,且 ,,连接 ,,,,且 , 分别交 于 ,.
(1)四边形 是何种特殊四边形 请证明你的结论;
(2)当 与 相切时,四边形 是正方形吗 请说明理由.
22. 如图,在半径为 的 中,直径 与弦 相交于点 , 交 的延长线于 ,连接 .
(1)若 的长为 ,求 的度数;
(2)若 ,,,求 的值.
23. 如图,点 为 外接圆上的一动点(点 不在 上,且不与点 , 重合),.
(1)求证: 是该外接圆的直径;
(2)连接 ,求证:;
(3)若 关于直线 的对称图形为 ,连接 ,试探究 ,, 三者之间满足的等量关系,并证明你的结论.
24. 如图,半圆 的直径 ,以长为 的弦 为直径,向点 方向作半圆 ,其中 点在 上且不与 点重合,但 点可与 点重合.(注:结果保留 ,,)
(1)发现: 的长与 的长之和为定值 ,求 .
(2)思考:点 与 的最大距离为 ,此时点 , 间的距离为 ;
点 与 的最小距离为 ,此时半圆 的弧与 所围成的封闭图形面积为 ;
(3)探究:当半圆 与 相切时,求 的长.
答案
1. B
2. B
3. C
4. D
5. B
6. A
7. B
8. A
9. A
10. D
11.
12.
13.
14.
15. ①②③
16. 或
17. (1) 四边形 是正方形,
,
.
为 的中点,
,
,
.
(2) 连接 ,,.
,
.
正方形 内接于 ,
,
.
由弧长公式得 的长
18. (1) 连接 ,,作 于 ,
因为 是等边三角形,
所以 ,
所以 .
因为 ,,
所以 ,
所以 ,
所以 半径 .
(2) 因为由()知 ,,
所以 ,
所以 的长为 .
弓形 的面积为 .
19. (1) 连接 .
与 相切于点 , 与 相切于点 ,
,
,
,
,
是直径,
,
,
.
(2) 过点 作 于 .
在 中,
,,
,
,
.
,
,
,,
,
,
.
,
,
,,,
,
.
20. (1) 如图,连接 ,,
为 的直径,
是直角三角形,
为 的中点,
,
,
,
,
,
,
,即 ,
是 的切线.
(2) 设 的半径为 ,
,
,即 ,
解得:,
的直径为 .
21. (1) 四边形 是矩形.
证明:
因为 是 的直径,
所以 .
因为 是 的直径,
所以 .
因为 ,
所以四边形 是平行四边形,
所以 ,
所以 ,
所以 ,
所以四边形 是矩形.
(2) 四边形 是正方形,
理由:
因为 是 的切线, 是直径,
所以 .
在 中,,,,
所以 ,则 ,,
所以 ,
所以矩形 是正方形.
22. (1) 连接 ,
因为 的长为 , 的周长 ,
所以 ,
所以 .
(2) 连接 ,
因为 ,
所以 .
因为 ,
所以 ,
所以 .
因为 ,
所以设 ,,
所以 ,
所以 .
因为 是 的直径,
所以 ,
因为 ,
所以 .
因为 ,
所以 ,
所以 ,即 ,
所以 ,(不合题意,舍去),
所以 ,
所以 .
23. (1) ,
.
,
.
.
是该外接圆的直径.
(2) 如图所示作 ,延长 交 于点 .
,,
为等腰直角三角形.
.
由勾股定理,得 ,
.
由(1)可知 为等腰直角三角形,
,.
,
.
.
在 和 中,
.
.
.
(3) .
延长 交圆于点 ,连接 ,.
,
在 中,,.
.
,
.
,
,即 .
.
为直径,
.
在 中,,
.
24. (1) 如图 ,连接 ,.
,
.
,
是等边三角形,
,
的长为 .
半圆 的长为 ,
,
.
(2) ;
【解析】如图 ,过点 作 于点 ,连接 .
,,
由勾股定理可知 .
当 与 重合时, 与 的距离最大,最大值为 .
连接 ,此时,,
.
,
是等边三角形,
.
如图 ,当 与 重合时,设此时半圆 与 交于点 ,.连接 .
,
,此时, 与 的距离最小,最小值为 .
,
是等边三角形,
,
扇形 的面积为 .
的面积为 ,
半圆 的弧与 所围成的封闭图形面积为 .
(3) 当半圆 与 相切时,此时 .
如图 ,
当点 在线段 上时,在 中,由勾股定理可求得 ,
,
.
,
,
的长为 .
当点 在线段 上时,
此时 .
,
.
的长为 .
综上所述,当半圆 与 相切时, 的长为 或 .
一、选择题(共10小题)
1. 是 外一点,, 分别交 于 , 两点,已知 , 的度数分别为 ,,则 的度数为
A. B. C. D.
2. 下列说法正确的是
A. 三点确定一个圆
B. 一个三角形只有一个外接圆
C. 和半径垂直的直线是圆的切线
D. 三角形的内心到三角形三个顶点距离相等
3. 如图, 是圆 的直径,,, 是圆 的弦,且 ,则 等于
A. B. C. D.
4. 已知 的半径为 ,圆心到点 的距离为 ,且 , 分别是方程 的两根,则点 与 的位置关系是
A. 点 在 内部 B. 点 在 上
C. 点 在 外部 D. 点 不在 上
5. 在 中,,,, 的内心与顶点 的距离为
A. B. C. D.
6. 如图, 的外切正六边形 的边长为 ,则图中阴影部分的面积为
A. B. C. D.
7. 如图, 为 的切线, 为切点,若 ,, 为圆周上两点,且 ,则 等于
A. B. C. D.
8. 如图,在 中,,,即将 绕点 逆时针旋转 后得到 ,点 经过的路径为 ,则图中阴影部分的面积是
A. B. C. D.
9. 如图,圆内接四边形 的边 过圆心 ,过点 的切线与边 所在直线垂直于点 ,若 ,则 等于
A. B. C. D.
10. 如图, 是 的直径,, 是 上的点,且 , 分别与 , 相交于点 ,,则下列结论:;; 平分 ;;;,其中一定成立的是
A. B. C. D.
二、填空题(共6小题)
11. 如图,, 是 的半径,点 在 上,连接 ,,若 ,则 度.
12. 将一条长为 的线段绕着中点旋转 ,该线段所扫过的面积是 .
13. 如图, 为 的弦,直径 为 , 于 ,,则 的长为 (结果保留 ).
14. 如图, 是 的半径,弦 于 ,若 ,则 度.
15. 如图所示, 切 于 , 切 于 , 交 于 ,下列说法:① ,② ,③ 垂直平分 ,其中正确说法的序号是 .
16. 如图,直线 分别交 轴, 轴于点 ,,点 为 轴上的点,若以点 为圆心, 长为半径的圆与直线 相切时,则点 的坐标为 .
三、解答题(共8小题)
17. 如图,正方形 内接于 , 为 的中点,连接 ,.
(1)求证:;
(2)当 的半径为 时,求 的长.
18. 如图,已知边长为 的等边 内接于 .
(1)求 的半径;
(2)求 的长和弓形 的面积.
19. 如图, 与 的直角边 和斜边 分别相切于点 ,,与边 相交于点 , 与 相交于点 ,连接 并延长交 边于点 .
(1)求证:;
(2)若 ,,求 的长.
20. 如图,在 中,,以 为直径作 交 于点 , 为 的中点,连接 并延长交 的延长线于点 .
(1)求证: 是 的切线;
(2)若 ,,求 直径的长.
21. 如图, 是 的直径,线段 过圆心 ,且 ,,连接 ,,,,且 , 分别交 于 ,.
(1)四边形 是何种特殊四边形 请证明你的结论;
(2)当 与 相切时,四边形 是正方形吗 请说明理由.
22. 如图,在半径为 的 中,直径 与弦 相交于点 , 交 的延长线于 ,连接 .
(1)若 的长为 ,求 的度数;
(2)若 ,,,求 的值.
23. 如图,点 为 外接圆上的一动点(点 不在 上,且不与点 , 重合),.
(1)求证: 是该外接圆的直径;
(2)连接 ,求证:;
(3)若 关于直线 的对称图形为 ,连接 ,试探究 ,, 三者之间满足的等量关系,并证明你的结论.
24. 如图,半圆 的直径 ,以长为 的弦 为直径,向点 方向作半圆 ,其中 点在 上且不与 点重合,但 点可与 点重合.(注:结果保留 ,,)
(1)发现: 的长与 的长之和为定值 ,求 .
(2)思考:点 与 的最大距离为 ,此时点 , 间的距离为 ;
点 与 的最小距离为 ,此时半圆 的弧与 所围成的封闭图形面积为 ;
(3)探究:当半圆 与 相切时,求 的长.
答案
1. B
2. B
3. C
4. D
5. B
6. A
7. B
8. A
9. A
10. D
11.
12.
13.
14.
15. ①②③
16. 或
17. (1) 四边形 是正方形,
,
.
为 的中点,
,
,
.
(2) 连接 ,,.
,
.
正方形 内接于 ,
,
.
由弧长公式得 的长
18. (1) 连接 ,,作 于 ,
因为 是等边三角形,
所以 ,
所以 .
因为 ,,
所以 ,
所以 ,
所以 半径 .
(2) 因为由()知 ,,
所以 ,
所以 的长为 .
弓形 的面积为 .
19. (1) 连接 .
与 相切于点 , 与 相切于点 ,
,
,
,
,
是直径,
,
,
.
(2) 过点 作 于 .
在 中,
,,
,
,
.
,
,
,,
,
,
.
,
,
,,,
,
.
20. (1) 如图,连接 ,,
为 的直径,
是直角三角形,
为 的中点,
,
,
,
,
,
,
,即 ,
是 的切线.
(2) 设 的半径为 ,
,
,即 ,
解得:,
的直径为 .
21. (1) 四边形 是矩形.
证明:
因为 是 的直径,
所以 .
因为 是 的直径,
所以 .
因为 ,
所以四边形 是平行四边形,
所以 ,
所以 ,
所以 ,
所以四边形 是矩形.
(2) 四边形 是正方形,
理由:
因为 是 的切线, 是直径,
所以 .
在 中,,,,
所以 ,则 ,,
所以 ,
所以矩形 是正方形.
22. (1) 连接 ,
因为 的长为 , 的周长 ,
所以 ,
所以 .
(2) 连接 ,
因为 ,
所以 .
因为 ,
所以 ,
所以 .
因为 ,
所以设 ,,
所以 ,
所以 .
因为 是 的直径,
所以 ,
因为 ,
所以 .
因为 ,
所以 ,
所以 ,即 ,
所以 ,(不合题意,舍去),
所以 ,
所以 .
23. (1) ,
.
,
.
.
是该外接圆的直径.
(2) 如图所示作 ,延长 交 于点 .
,,
为等腰直角三角形.
.
由勾股定理,得 ,
.
由(1)可知 为等腰直角三角形,
,.
,
.
.
在 和 中,
.
.
.
(3) .
延长 交圆于点 ,连接 ,.
,
在 中,,.
.
,
.
,
,即 .
.
为直径,
.
在 中,,
.
24. (1) 如图 ,连接 ,.
,
.
,
是等边三角形,
,
的长为 .
半圆 的长为 ,
,
.
(2) ;
【解析】如图 ,过点 作 于点 ,连接 .
,,
由勾股定理可知 .
当 与 重合时, 与 的距离最大,最大值为 .
连接 ,此时,,
.
,
是等边三角形,
.
如图 ,当 与 重合时,设此时半圆 与 交于点 ,.连接 .
,
,此时, 与 的距离最小,最小值为 .
,
是等边三角形,
,
扇形 的面积为 .
的面积为 ,
半圆 的弧与 所围成的封闭图形面积为 .
(3) 当半圆 与 相切时,此时 .
如图 ,
当点 在线段 上时,在 中,由勾股定理可求得 ,
,
.
,
,
的长为 .
当点 在线段 上时,
此时 .
,
.
的长为 .
综上所述,当半圆 与 相切时, 的长为 或 .
