2022—2023学年湘教版数学七年级下册第1章二元一次方程组巩固练习(含答案)
文档属性
| 名称 | 2022—2023学年湘教版数学七年级下册第1章二元一次方程组巩固练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 261.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-18 07:46:25 | ||
图片预览


文档简介
第1章 二元一次方程组巩固练习
一、单选题
1.下列方程中,是二元一次方程的是( )
A. B. C. D.
2.下列方程组中,表示二元一次方程组的是( )
A. B. C. D.
3.二元一次方程组 的解是( )
A. B.
C. D.
4.小敏计划购买一批规格相同的花盆来养花,在商店里选购时,她先将个花盆叠在一起量得其高度是,再将个花盆叠在一起量得其高度是(如图所示).若把个相同规格的花盆叠在一起,则其高度是( )
A. B. C. D.
5.下列说法中正确的是( )
A.是方程3x-4y=1的一组解
B.方程3x-4y=1有无数组解,即x、y可以取任何数值
C.方程3x-4y=1只有两组解,两组解分别是: 、
D.方程3x-4y=1可能无解
6.若二元一次联立方程式的解为,,则之值为何?( )
A. B. C.5 D.25
7.已知是方程的一个解,则的值为( )
A. B. C. D.
8.当a、b都是整数时,我们称(a,b)为一个有序整数对,如(-2,2)和(2,-2)是两个不同的有序整数对,则满足|a-b|+|ab|=1的有序整数对有( )
A.2个 B.3个 C.4个 D.6个
9.已知是二元一次方程组的解,则的值为( ).
A.5 B.4 C.8 D.6
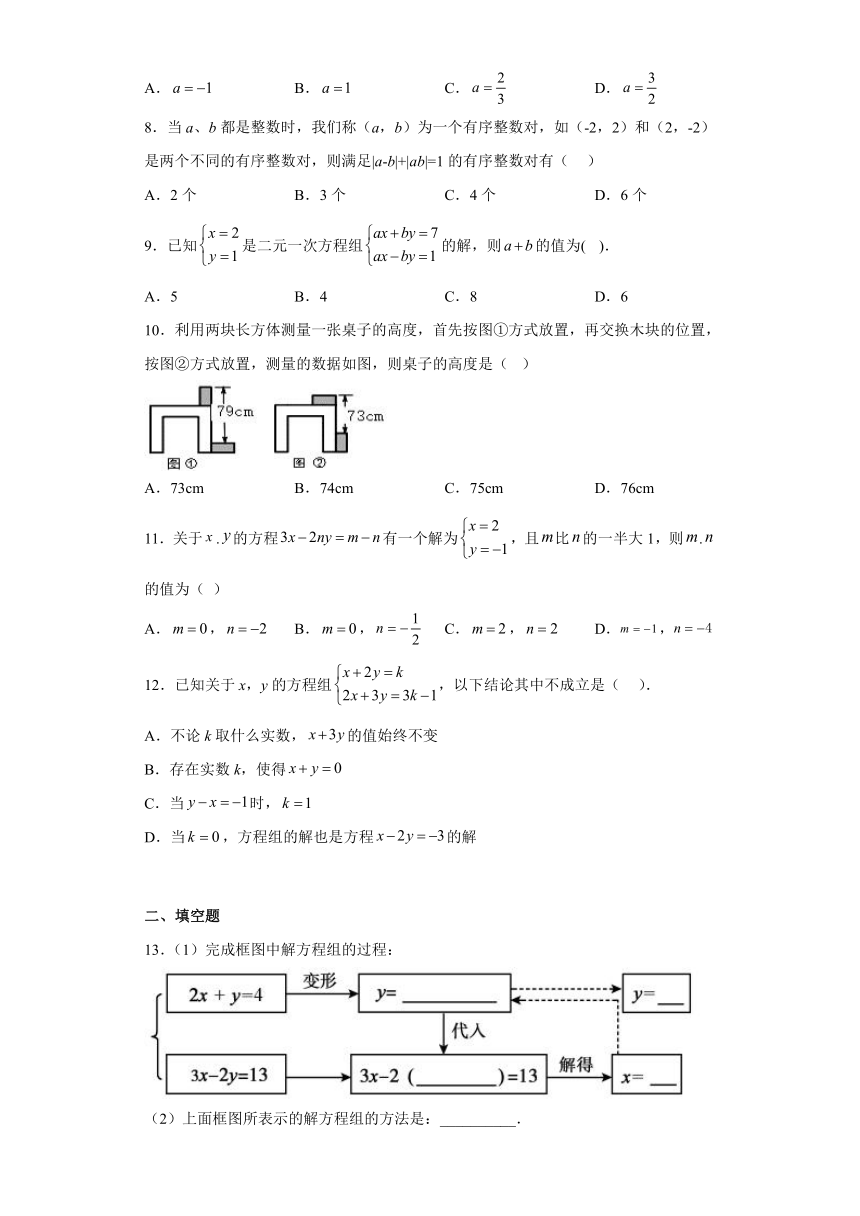
10.利用两块长方体测量一张桌子的高度,首先按图①方式放置,再交换木块的位置,按图②方式放置,测量的数据如图,则桌子的高度是( )
A.73cm B.74cm C.75cm D.76cm
11.关于.的方程有一个解为,且比的一半大1,则.的值为( )
A., B., C., D.,
12.已知关于x,y的方程组,以下结论其中不成立是( ).
A.不论k取什么实数,的值始终不变
B.存在实数k,使得
C.当时,
D.当,方程组的解也是方程的解
二、填空题
13.(1)完成框图中解方程组的过程:
(2)上面框图所表示的解方程组的方法是:__________.
14.请你写出一个二元一次方程组,使它的解为,这个方程组是____(答案不唯一).
15.已知是方程的解,则的值是___.
16.由方程组可得x与y之间的关系式是______(用含x的代数式表示y).
17.若关于x,y的方程组的解满足,则m的值是______.
18.对于实数x,y定义新运算其中a,b,c为常数,若,且有一个非零常数d,使得对于任意的x,恒有,则d的值是____.
三、解答题
19.疫情期间,学校为了学生在班级将生活垃圾和废弃口罩分类丢弃,准备购买A,B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需270元,购买2个A型垃圾箱比购买3个B型垃圾箱少用80元.求每个A型垃圾箱和B型垃圾箱各多少元?学校购买A型垃圾桶8个,B型垃圾桶16个,共花费多少元?
20.某校组织“大手拉小手,义卖献爱心”活动,计划从批发市场花4500元购买了黑白两种颜色的文化衫200件,组织人员手绘设计后出售,并将所获利润全部捐给山区困难孩子.每件文化衫的批发价及手绘后的零售价如表:
批发价(元) 零售价(元)
黑色文化衫 30 50
白色文化衫 20 45
(1)学校购进黑、白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.
21.列方程组,解应用题.“阅读与人文滋养内心”,某校开展阅读经典活动.小明天里阅读的总页数比小颖天里阅读的总页数少页,小颖平均每天阅读的页数比小明平均每天分别阅读的页数的倍少页,求小明和小颖平均每天阅读的天数.
22.在二元一次方程中,若x,y互为相反数,求x与y的值.
23.自农村义务教育学日营养改蓉计划开新以来.某校七年拨(d)班某天早上分到牛奶、面包共7件,每件牛奶24元,每件面包16元,共14元,该班分到牛奶、面包各多少件?
24.冬季来临,某网店准备在厂家购进A、B两种暖手宝共100个用于销售,若购买A种暖手宝8个,B种暖手宝3个,需要950元,若购买A种暖手宝5个,B种暖手宝6个,则需要800元.
(1)购买A,B两种暖手宝每个各需多少元?
(2)①由于资金限制,用于购买这两种暖手宝的资金不能超过7650元,设购买A种暖手宝m个,求m的取值范围;
②在①的条件下,购进A种暖手宝不能少于50个,则有哪几种购买方案?
(3)购买后,若一个A种暖手宝运费为5元,一个B种暖手宝运费为4元,在第(2)各种购买方案中,购买100个暖手宝,哪一种购买方案所付的运费最少?最少运费多少元?
参考答案
1.C
2.D
3.B
4.A
5.A
6.D
7.B
8.D
9.A
10.D
11.A
12.D
13.解:(1)填写如下:
(2)框图所表示的解方程组的方法是:代入消元法,
故答案为:代入消元法.
14.等,(答案不唯一).
15.-2
16.
17.
18.4
19解:设A型垃圾箱每个x元,B型垃圾箱每个y元,依题意列方程组得:
,
解之得:,
故A型垃圾桶每个50元,B型垃圾桶每个60元;
学校购买A型垃圾桶8个,B型垃圾桶16个,共花费8×50+16×60=1360元.
20.(1)解:设学校购进黑文化衫x件,白文化衫y件.
根据题意,得,解得.
答:学校购进黑文化衫50件,白文化衫150件.
(2)(元)
答:该校这次义卖活动共获得4750元利润.
21.解:设小明平均每天阅读页,小颖平均每天阅读页.
根据题意,得,
得.
答:小明平均每天阅读8页,小颖平均每天阅读6页.
22.解:根据题意得:
∴5x-3y+(x+y)×3,得.
∴.
把代入②,得.
∴,.
23.设该班分到牛场z件,面包y件,由题意,得
,
解得,
答:该班分到牛奶4件,面包3件.
24.解:(1)设购买A种暖手宝每个需x元,购买B种暖手宝每个需y元,由题意得:
解得:.
故购买A种暖手宝每个需100元,购买B种暖手宝每个需50元.
(2)①设购买A种暖手宝m个,则购买B种暖手宝(100﹣m)个,由题意得:
100m+50(100﹣m)≤7650
解得:m≤53,
∵m≥0
故m的取值范围为:0≤m≤53
②∵购进A种暖手宝不能少于50个
∴50≤m≤53
故有四种购买方案,分别为:
A种购买50个,B种购买50个;A种购买51个,B种购买49个;
A种购买52个,B种购买48个;A种购买53个,B种购买47个.
(3)令两种暖手宝的运费为w,则w=5m+4(100﹣m)
即w=m+400(50≤m≤53)
由一次函数的性质可知w随m的增大而增大,
因此当m=50时,函数取最小值,即w=50+400=450.
故当A种购买50个,B种购买50个时运费最少,为450元.
一、单选题
1.下列方程中,是二元一次方程的是( )
A. B. C. D.
2.下列方程组中,表示二元一次方程组的是( )
A. B. C. D.
3.二元一次方程组 的解是( )
A. B.
C. D.
4.小敏计划购买一批规格相同的花盆来养花,在商店里选购时,她先将个花盆叠在一起量得其高度是,再将个花盆叠在一起量得其高度是(如图所示).若把个相同规格的花盆叠在一起,则其高度是( )
A. B. C. D.
5.下列说法中正确的是( )
A.是方程3x-4y=1的一组解
B.方程3x-4y=1有无数组解,即x、y可以取任何数值
C.方程3x-4y=1只有两组解,两组解分别是: 、
D.方程3x-4y=1可能无解
6.若二元一次联立方程式的解为,,则之值为何?( )
A. B. C.5 D.25
7.已知是方程的一个解,则的值为( )
A. B. C. D.
8.当a、b都是整数时,我们称(a,b)为一个有序整数对,如(-2,2)和(2,-2)是两个不同的有序整数对,则满足|a-b|+|ab|=1的有序整数对有( )
A.2个 B.3个 C.4个 D.6个
9.已知是二元一次方程组的解,则的值为( ).
A.5 B.4 C.8 D.6
10.利用两块长方体测量一张桌子的高度,首先按图①方式放置,再交换木块的位置,按图②方式放置,测量的数据如图,则桌子的高度是( )
A.73cm B.74cm C.75cm D.76cm
11.关于.的方程有一个解为,且比的一半大1,则.的值为( )
A., B., C., D.,
12.已知关于x,y的方程组,以下结论其中不成立是( ).
A.不论k取什么实数,的值始终不变
B.存在实数k,使得
C.当时,
D.当,方程组的解也是方程的解
二、填空题
13.(1)完成框图中解方程组的过程:
(2)上面框图所表示的解方程组的方法是:__________.
14.请你写出一个二元一次方程组,使它的解为,这个方程组是____(答案不唯一).
15.已知是方程的解,则的值是___.
16.由方程组可得x与y之间的关系式是______(用含x的代数式表示y).
17.若关于x,y的方程组的解满足,则m的值是______.
18.对于实数x,y定义新运算其中a,b,c为常数,若,且有一个非零常数d,使得对于任意的x,恒有,则d的值是____.
三、解答题
19.疫情期间,学校为了学生在班级将生活垃圾和废弃口罩分类丢弃,准备购买A,B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需270元,购买2个A型垃圾箱比购买3个B型垃圾箱少用80元.求每个A型垃圾箱和B型垃圾箱各多少元?学校购买A型垃圾桶8个,B型垃圾桶16个,共花费多少元?
20.某校组织“大手拉小手,义卖献爱心”活动,计划从批发市场花4500元购买了黑白两种颜色的文化衫200件,组织人员手绘设计后出售,并将所获利润全部捐给山区困难孩子.每件文化衫的批发价及手绘后的零售价如表:
批发价(元) 零售价(元)
黑色文化衫 30 50
白色文化衫 20 45
(1)学校购进黑、白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.
21.列方程组,解应用题.“阅读与人文滋养内心”,某校开展阅读经典活动.小明天里阅读的总页数比小颖天里阅读的总页数少页,小颖平均每天阅读的页数比小明平均每天分别阅读的页数的倍少页,求小明和小颖平均每天阅读的天数.
22.在二元一次方程中,若x,y互为相反数,求x与y的值.
23.自农村义务教育学日营养改蓉计划开新以来.某校七年拨(d)班某天早上分到牛奶、面包共7件,每件牛奶24元,每件面包16元,共14元,该班分到牛奶、面包各多少件?
24.冬季来临,某网店准备在厂家购进A、B两种暖手宝共100个用于销售,若购买A种暖手宝8个,B种暖手宝3个,需要950元,若购买A种暖手宝5个,B种暖手宝6个,则需要800元.
(1)购买A,B两种暖手宝每个各需多少元?
(2)①由于资金限制,用于购买这两种暖手宝的资金不能超过7650元,设购买A种暖手宝m个,求m的取值范围;
②在①的条件下,购进A种暖手宝不能少于50个,则有哪几种购买方案?
(3)购买后,若一个A种暖手宝运费为5元,一个B种暖手宝运费为4元,在第(2)各种购买方案中,购买100个暖手宝,哪一种购买方案所付的运费最少?最少运费多少元?
参考答案
1.C
2.D
3.B
4.A
5.A
6.D
7.B
8.D
9.A
10.D
11.A
12.D
13.解:(1)填写如下:
(2)框图所表示的解方程组的方法是:代入消元法,
故答案为:代入消元法.
14.等,(答案不唯一).
15.-2
16.
17.
18.4
19解:设A型垃圾箱每个x元,B型垃圾箱每个y元,依题意列方程组得:
,
解之得:,
故A型垃圾桶每个50元,B型垃圾桶每个60元;
学校购买A型垃圾桶8个,B型垃圾桶16个,共花费8×50+16×60=1360元.
20.(1)解:设学校购进黑文化衫x件,白文化衫y件.
根据题意,得,解得.
答:学校购进黑文化衫50件,白文化衫150件.
(2)(元)
答:该校这次义卖活动共获得4750元利润.
21.解:设小明平均每天阅读页,小颖平均每天阅读页.
根据题意,得,
得.
答:小明平均每天阅读8页,小颖平均每天阅读6页.
22.解:根据题意得:
∴5x-3y+(x+y)×3,得.
∴.
把代入②,得.
∴,.
23.设该班分到牛场z件,面包y件,由题意,得
,
解得,
答:该班分到牛奶4件,面包3件.
24.解:(1)设购买A种暖手宝每个需x元,购买B种暖手宝每个需y元,由题意得:
解得:.
故购买A种暖手宝每个需100元,购买B种暖手宝每个需50元.
(2)①设购买A种暖手宝m个,则购买B种暖手宝(100﹣m)个,由题意得:
100m+50(100﹣m)≤7650
解得:m≤53,
∵m≥0
故m的取值范围为:0≤m≤53
②∵购进A种暖手宝不能少于50个
∴50≤m≤53
故有四种购买方案,分别为:
A种购买50个,B种购买50个;A种购买51个,B种购买49个;
A种购买52个,B种购买48个;A种购买53个,B种购买47个.
(3)令两种暖手宝的运费为w,则w=5m+4(100﹣m)
即w=m+400(50≤m≤53)
由一次函数的性质可知w随m的增大而增大,
因此当m=50时,函数取最小值,即w=50+400=450.
故当A种购买50个,B种购买50个时运费最少,为450元.
