2022—2023学年北师大版数学七年级下册 4.3探索三角形全等的条件同步练习(无答案)
文档属性
| 名称 | 2022—2023学年北师大版数学七年级下册 4.3探索三角形全等的条件同步练习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 299.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-18 00:00:00 | ||
图片预览


文档简介
4.3 探索三角形全等的条件
一、单选题
1.如图,已知△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为( )
A.2 B.3 C.2或3 D.1或5
2.如图,已知中,,,分别是边的中点,,边上的动点,的最小值为( )
A.7.5 B.6 C.4 D.不能确定
3.如图,点、分别在、上,、相交于点,若,则再添加一个条件,仍不能证明≌的是( )
A. B.
C. D.
4.用尺规作图法作已知角的平分线的步骤如下:①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;②分别以点D,E为圆心,以大于的长为半径作弧,两弧在的内部相交于点C;③作射线OC. 则射线OC为的平分线,由上述作法可得的依据是( )
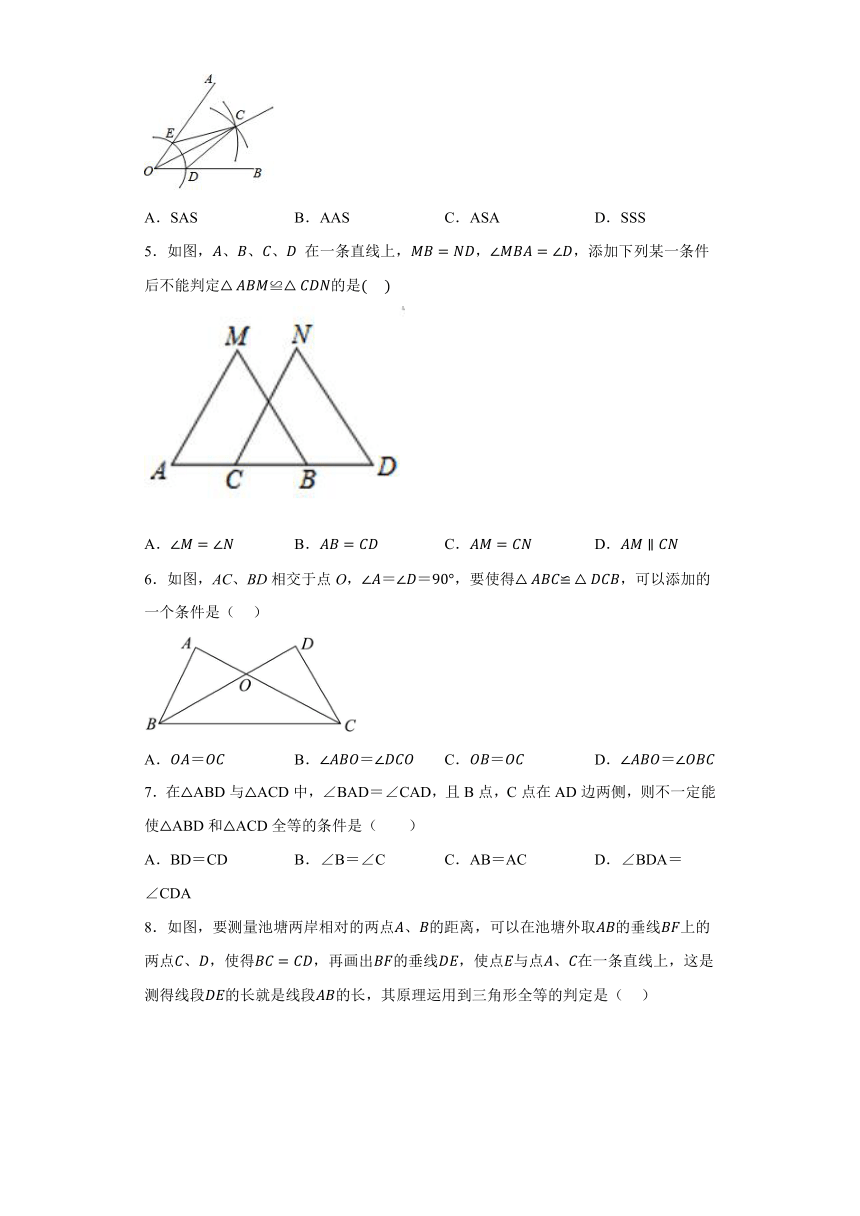
A.SAS B.AAS C.ASA D.SSS
5.如图,、、、 在一条直线上,,,添加下列某一条件后不能判定≌的是( )
A. B. C. D.
6.如图,AC、BD相交于点O,,要使得,可以添加的一个条件是( )
A. B. C. D.
7.在△ABD与△ACD中,∠BAD=∠CAD,且B点,C点在AD边两侧,则不一定能使△ABD和△ACD全等的条件是( )
A.BD=CD B.∠B=∠C C.AB=AC D.∠BDA=∠CDA
8.如图,要测量池塘两岸相对的两点、的距离,可以在池塘外取的垂线上的两点、,使得,再画出的垂线,使点与点、在一条直线上,这是测得线段的长就是线段的长,其原理运用到三角形全等的判定是( )
A. B. C. D.
9.如图,已知,添加下列条件后不能使的是( )
A. B. C. D.
10.如图,已知AB=DC,AC=DB,能直接判断△ABC≌△DCB的方法是( )
A.SAS B.AAS C.SSS D.ASA
二、填空题
11.如图,在△ABC中,∠A=90°,BD平分∠ABC,AD=2cm,DE⊥BC,则DE为___cm.
12.如图,已知的面积为14,BP平分,且于点P,则的面积是___________.
13.如图,AB与CD交于点O,AO=BO,CO=DO,若AC=3,CO=2,则BD=______.
14.如图,在中,,平分,于点,连接,若的面积为,则的面积为____.
15.如图,点,,,在同一直线上,,,如果直接依据“ASA”来判定,那么需要补充的条件是_______.
三、解答题
16.如图,已知在△ABC 和△ABD 中,AD = BC,∠DAB = ∠CBA,求证:∠C = ∠D.
17.已知:如图,点A,F,C,D在同一直线上,,,,
求证:.
18.如图 1,在平面直角坐标系中,A,B,D 三点的坐标是(0,2),(-2,0),(1,0),点C 是 x 轴下方一点,且 CD⊥AD,∠BAD+∠BCD=180°,AD=CD
(1)求证:BD 平分∠ABC
(2)求四边形 ABCD 的面积
(3)如图 2,BE 是∠ABO 的邻补角的平分线,连接 AE,OE 交 AB 于点 F,若∠AEO=45°,求证:AF=AO.
19.已知△ABC和△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点D等腰直角三角形ABC斜边AB所在直线上一点(不与点B重合).
(1)如图1,当点D在线段AB上时,直接写出DA2,DB2,DE2三者之间的数量关系:________;
(2)如图2,当点D在线段AB的延长线上时,(1)中的结论仍然成立,请你利用图2给出证明过程.
20.如图,∠ABC=∠DCB,BD、CA分别平分∠ABC、∠DCB.求证:AC=DB.
21.已知:如图,AB∥CD,AB=CD.求证:AD∥BC.
证明:∵ AB∥CD,
∴ ∠______=∠______ ( )
在△______和△______中,
∴ Δ______≌Δ______ ( ).
∴ ∠_____=∠____ ( )
∴ ______∥______ ( )
一、单选题
1.如图,已知△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为( )
A.2 B.3 C.2或3 D.1或5
2.如图,已知中,,,分别是边的中点,,边上的动点,的最小值为( )
A.7.5 B.6 C.4 D.不能确定
3.如图,点、分别在、上,、相交于点,若,则再添加一个条件,仍不能证明≌的是( )
A. B.
C. D.
4.用尺规作图法作已知角的平分线的步骤如下:①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;②分别以点D,E为圆心,以大于的长为半径作弧,两弧在的内部相交于点C;③作射线OC. 则射线OC为的平分线,由上述作法可得的依据是( )
A.SAS B.AAS C.ASA D.SSS
5.如图,、、、 在一条直线上,,,添加下列某一条件后不能判定≌的是( )
A. B. C. D.
6.如图,AC、BD相交于点O,,要使得,可以添加的一个条件是( )
A. B. C. D.
7.在△ABD与△ACD中,∠BAD=∠CAD,且B点,C点在AD边两侧,则不一定能使△ABD和△ACD全等的条件是( )
A.BD=CD B.∠B=∠C C.AB=AC D.∠BDA=∠CDA
8.如图,要测量池塘两岸相对的两点、的距离,可以在池塘外取的垂线上的两点、,使得,再画出的垂线,使点与点、在一条直线上,这是测得线段的长就是线段的长,其原理运用到三角形全等的判定是( )
A. B. C. D.
9.如图,已知,添加下列条件后不能使的是( )
A. B. C. D.
10.如图,已知AB=DC,AC=DB,能直接判断△ABC≌△DCB的方法是( )
A.SAS B.AAS C.SSS D.ASA
二、填空题
11.如图,在△ABC中,∠A=90°,BD平分∠ABC,AD=2cm,DE⊥BC,则DE为___cm.
12.如图,已知的面积为14,BP平分,且于点P,则的面积是___________.
13.如图,AB与CD交于点O,AO=BO,CO=DO,若AC=3,CO=2,则BD=______.
14.如图,在中,,平分,于点,连接,若的面积为,则的面积为____.
15.如图,点,,,在同一直线上,,,如果直接依据“ASA”来判定,那么需要补充的条件是_______.
三、解答题
16.如图,已知在△ABC 和△ABD 中,AD = BC,∠DAB = ∠CBA,求证:∠C = ∠D.
17.已知:如图,点A,F,C,D在同一直线上,,,,
求证:.
18.如图 1,在平面直角坐标系中,A,B,D 三点的坐标是(0,2),(-2,0),(1,0),点C 是 x 轴下方一点,且 CD⊥AD,∠BAD+∠BCD=180°,AD=CD
(1)求证:BD 平分∠ABC
(2)求四边形 ABCD 的面积
(3)如图 2,BE 是∠ABO 的邻补角的平分线,连接 AE,OE 交 AB 于点 F,若∠AEO=45°,求证:AF=AO.
19.已知△ABC和△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,点D等腰直角三角形ABC斜边AB所在直线上一点(不与点B重合).
(1)如图1,当点D在线段AB上时,直接写出DA2,DB2,DE2三者之间的数量关系:________;
(2)如图2,当点D在线段AB的延长线上时,(1)中的结论仍然成立,请你利用图2给出证明过程.
20.如图,∠ABC=∠DCB,BD、CA分别平分∠ABC、∠DCB.求证:AC=DB.
21.已知:如图,AB∥CD,AB=CD.求证:AD∥BC.
证明:∵ AB∥CD,
∴ ∠______=∠______ ( )
在△______和△______中,
∴ Δ______≌Δ______ ( ).
∴ ∠_____=∠____ ( )
∴ ______∥______ ( )
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
