人教版九年级数学上册第二十三章旋转单元检测(含解析)
文档属性
| 名称 | 人教版九年级数学上册第二十三章旋转单元检测(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1020.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-18 13:06:04 | ||
图片预览

文档简介
人教版 第二十三章 旋转 单元检测
一、选择题(共13小题)
1. 下列图形中,既是中心对称图形,又是轴对称图形的是
A. B.
C. D.
2. 下列运动形式属于旋转的是
A. 在空中上升的氢气球 B. 飞驰的火车
C. 时钟上钟摆的摆动 D. 运动员掷出的标枪
3. 下列图形中,是轴对称图形,但不是中心对称图形的是
A. B.
C. D.
4. 下列运动属于旋转的是
A. 火箭升空的运动 B. 足球在草地上滚动
C. 大风车运动的过程 D. 传输带上物体运输的过程
5. 在如图所示的方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,该小正方形的序号是
A. ① B. ② C. ③ D. ④
6. 如果某图形绕它的中心旋转 后能与自身重合,则该图形
A. 是中心对称图形,但不是旋转对称图形
B. 是旋转对称图形,但不一定是中心对称图形
C. 既是中心对称图形,又是旋转对称图形
D. 既不是中心对称图形,也不是旋转对称图形
7. 如图,在 的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是
A. 点 B. 点 C. 点 D. 点
8. 如图,将 绕点 顺时针旋转 得到 ,则点 的坐标是
A. B. C. D.
9. 下列图形中是旋转对称图形,但不是中心对称图形的有
A. 个 B. 个 C. 个 D. 个
10. 年冬季奥运会将在北京和张家口举行,如图所示的滑雪人经过旋转不能得到的是
A. B.
C. D.
11. 如图,在平行四边形 中, 于点 ,将 绕点 顺时针旋转,得到 ,点 在 边上,连接 .如果 ,,那么 的大小为
A. B. C. D.
12. 如图,在等边三角形 中,在 边上取两点 ,,使 .若 ,,,则以 ,, 为边长的三角形的形状为
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 随 ,, 的值而定
13. 如图,在平行四边形 中,对角线 和 相交于点 .下列结论:① ;② ;③ ;④平行四边形既是轴对称图形又是中心对称图形,其中一定正确的个数是
A. B. C. D.
二、填空题(共6小题)
14. 图形运动指图形的 、 、 三种运动.图形经过这三种基本运动,位置发生变化,但是形状、大小保持 .反之,形状、大小相同的图形经过图形的运动一定能够 .
15. 在平面内,图形绕着 按照 ,这样的运动叫做 ,这个定点叫做 ,转动的角度叫做 .
16. 观察下列图形,将其中的旋转对称图形和中心对称图形所对应的编号填入相应的横线里.
()旋转对称图形 .
()中心对称图形 .
17. 下列图中是中心对称图形的有 .
18. 如图,在正方形网格中,线段 可以看作是线段 经过若干次图形的变化(平移、旋转、轴对称)得到的,写出一种由线段 得到线段 的过程: .
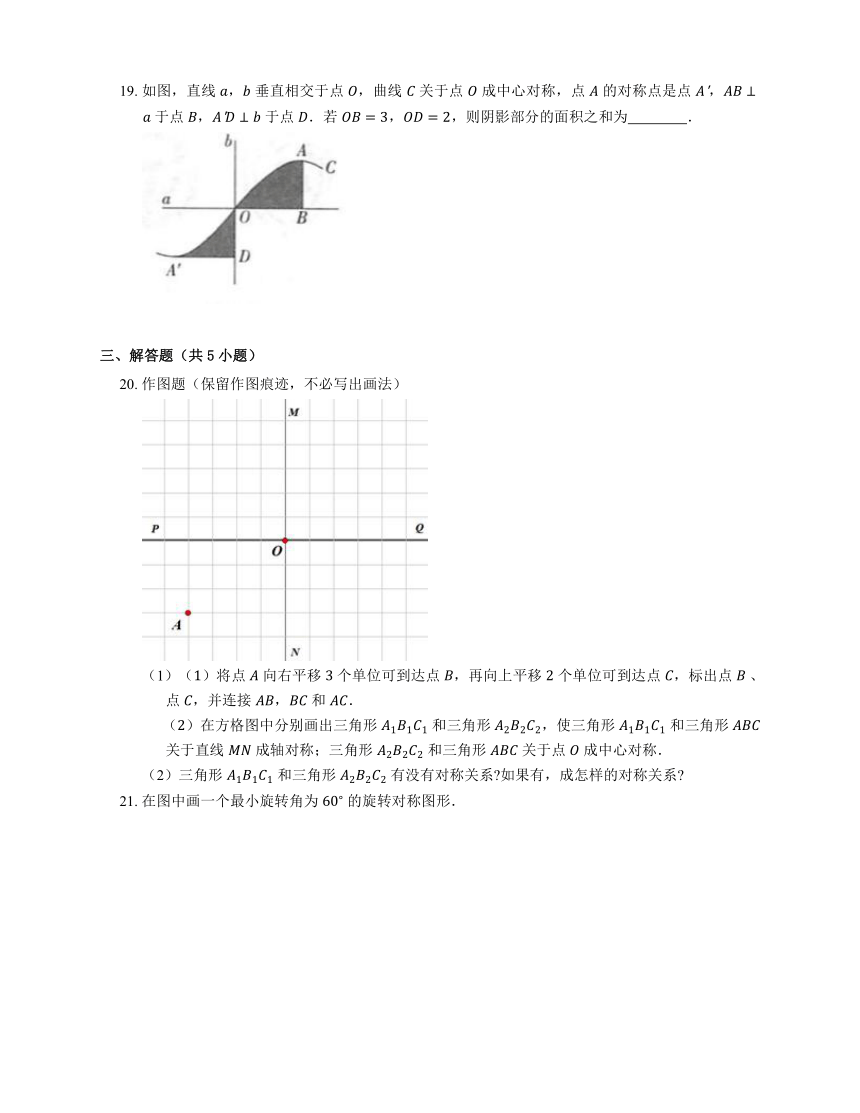
19. 如图,直线 , 垂直相交于点 ,曲线 关于点 成中心对称,点 的对称点是点 , 于点 , 于点 .若 ,,则阴影部分的面积之和为 .
三、解答题(共5小题)
20. 作图题(保留作图痕迹,不必写出画法)
(1)()将点 向右平移 个单位可到达点 ,再向上平移 个单位可到达点 ,标出点 、点 ,并连接 , 和 .
()在方格图中分别画出三角形 和三角形 ,使三角形 和三角形 关于直线 成轴对称;三角形 和三角形 关于点 成中心对称.
(2)三角形 和三角形 有没有对称关系 如果有,成怎样的对称关系
21. 在图中画一个最小旋转角为 的旋转对称图形.
22. 如图,,,将 绕点 旋转至 ,使得点 恰好落在直线 上,在下图中画出旋转后的图形.
23. 如图,在等腰 中,,,且 .
(1)把 绕点 逆时针旋转 ,请画出旋转后的 的位置;
(2) 与 全等吗
(3)判断 是什么类型的三角形.
24. 用 块如图①所示正方形瓷砖,拼成一个新的正方形,请你在图②、图③、图④中各画一种拼法.要求:其中一个图形既是轴对称图形,又是中心对称图形;一个图形是轴对称图形,但不是中心对称图形;一个图形是中心对称图形,但不是轴对称图形.
答案
1. C
2. C
【解析】根据旋转的概念判断.
3. A
【解析】选项A,是轴对称图形,不是中心对称图形;选项B,只是中心对称图形;选项C,既是轴对称图形,又是中心对称图形;选项D,既不是轴对称图形,又不是中心对称图形.
4. C
【解析】根据旋转的定义可知,大风车运动的过程是旋转.
5. B
6. C
7. B
8. B
9. C
10. C
【解析】选项A、B、D中滑雪人都可以通过题图旋转得到,而选项C中滑雪人是题图通过翻折到的.
11. A
12. C
【解析】将 绕点 顺时针旋转 得到 .连接 .
是等边三角形,
,
,
,
,
,
,,
,
,
,,
,
,, 为边长的三角形 是钝角三角形,
故选:C.
13. B
【解析】根据平行四边形的性质可知,平行四边形的对角线互相平分,即 ,故①中的结论正确;
平行四边形的对角相等,即 ,故②中的结论正确;
平行四边形的对角线互相平分,不一定互相垂直,故③中的结论错误;
平行四边形是中心对称图形,但不一定是轴对称图形,故④中的结论错误.
14. 平移,旋转,翻折,不变,重合
15. 一个定点,某个方向转动一定大小的角 ,图形的旋转,旋转中心,旋转角
16. A,B,C,D,E,C,D
17. (1),(3)
18. 将线段 绕点 逆时针旋转 ,再向左平移 个单位长度
19.
【解析】由题意可知,阴影部分的面积之和为 .
20. (1) 略.
(2) 有.
三角形 和三角形 关于直线 成轴对称.
21. 略
22. 略
23. (1) 图略.
(2) 全等.
因为 ,
所以 ,,
因为 ,,
所以 ,
所以 ,
即 ,
可证 .
(3) 直角三角形.
24. 如图:
一、选择题(共13小题)
1. 下列图形中,既是中心对称图形,又是轴对称图形的是
A. B.
C. D.
2. 下列运动形式属于旋转的是
A. 在空中上升的氢气球 B. 飞驰的火车
C. 时钟上钟摆的摆动 D. 运动员掷出的标枪
3. 下列图形中,是轴对称图形,但不是中心对称图形的是
A. B.
C. D.
4. 下列运动属于旋转的是
A. 火箭升空的运动 B. 足球在草地上滚动
C. 大风车运动的过程 D. 传输带上物体运输的过程
5. 在如图所示的方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,该小正方形的序号是
A. ① B. ② C. ③ D. ④
6. 如果某图形绕它的中心旋转 后能与自身重合,则该图形
A. 是中心对称图形,但不是旋转对称图形
B. 是旋转对称图形,但不一定是中心对称图形
C. 既是中心对称图形,又是旋转对称图形
D. 既不是中心对称图形,也不是旋转对称图形
7. 如图,在 的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是
A. 点 B. 点 C. 点 D. 点
8. 如图,将 绕点 顺时针旋转 得到 ,则点 的坐标是
A. B. C. D.
9. 下列图形中是旋转对称图形,但不是中心对称图形的有
A. 个 B. 个 C. 个 D. 个
10. 年冬季奥运会将在北京和张家口举行,如图所示的滑雪人经过旋转不能得到的是
A. B.
C. D.
11. 如图,在平行四边形 中, 于点 ,将 绕点 顺时针旋转,得到 ,点 在 边上,连接 .如果 ,,那么 的大小为
A. B. C. D.
12. 如图,在等边三角形 中,在 边上取两点 ,,使 .若 ,,,则以 ,, 为边长的三角形的形状为
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 随 ,, 的值而定
13. 如图,在平行四边形 中,对角线 和 相交于点 .下列结论:① ;② ;③ ;④平行四边形既是轴对称图形又是中心对称图形,其中一定正确的个数是
A. B. C. D.
二、填空题(共6小题)
14. 图形运动指图形的 、 、 三种运动.图形经过这三种基本运动,位置发生变化,但是形状、大小保持 .反之,形状、大小相同的图形经过图形的运动一定能够 .
15. 在平面内,图形绕着 按照 ,这样的运动叫做 ,这个定点叫做 ,转动的角度叫做 .
16. 观察下列图形,将其中的旋转对称图形和中心对称图形所对应的编号填入相应的横线里.
()旋转对称图形 .
()中心对称图形 .
17. 下列图中是中心对称图形的有 .
18. 如图,在正方形网格中,线段 可以看作是线段 经过若干次图形的变化(平移、旋转、轴对称)得到的,写出一种由线段 得到线段 的过程: .
19. 如图,直线 , 垂直相交于点 ,曲线 关于点 成中心对称,点 的对称点是点 , 于点 , 于点 .若 ,,则阴影部分的面积之和为 .
三、解答题(共5小题)
20. 作图题(保留作图痕迹,不必写出画法)
(1)()将点 向右平移 个单位可到达点 ,再向上平移 个单位可到达点 ,标出点 、点 ,并连接 , 和 .
()在方格图中分别画出三角形 和三角形 ,使三角形 和三角形 关于直线 成轴对称;三角形 和三角形 关于点 成中心对称.
(2)三角形 和三角形 有没有对称关系 如果有,成怎样的对称关系
21. 在图中画一个最小旋转角为 的旋转对称图形.
22. 如图,,,将 绕点 旋转至 ,使得点 恰好落在直线 上,在下图中画出旋转后的图形.
23. 如图,在等腰 中,,,且 .
(1)把 绕点 逆时针旋转 ,请画出旋转后的 的位置;
(2) 与 全等吗
(3)判断 是什么类型的三角形.
24. 用 块如图①所示正方形瓷砖,拼成一个新的正方形,请你在图②、图③、图④中各画一种拼法.要求:其中一个图形既是轴对称图形,又是中心对称图形;一个图形是轴对称图形,但不是中心对称图形;一个图形是中心对称图形,但不是轴对称图形.
答案
1. C
2. C
【解析】根据旋转的概念判断.
3. A
【解析】选项A,是轴对称图形,不是中心对称图形;选项B,只是中心对称图形;选项C,既是轴对称图形,又是中心对称图形;选项D,既不是轴对称图形,又不是中心对称图形.
4. C
【解析】根据旋转的定义可知,大风车运动的过程是旋转.
5. B
6. C
7. B
8. B
9. C
10. C
【解析】选项A、B、D中滑雪人都可以通过题图旋转得到,而选项C中滑雪人是题图通过翻折到的.
11. A
12. C
【解析】将 绕点 顺时针旋转 得到 .连接 .
是等边三角形,
,
,
,
,
,
,,
,
,
,,
,
,, 为边长的三角形 是钝角三角形,
故选:C.
13. B
【解析】根据平行四边形的性质可知,平行四边形的对角线互相平分,即 ,故①中的结论正确;
平行四边形的对角相等,即 ,故②中的结论正确;
平行四边形的对角线互相平分,不一定互相垂直,故③中的结论错误;
平行四边形是中心对称图形,但不一定是轴对称图形,故④中的结论错误.
14. 平移,旋转,翻折,不变,重合
15. 一个定点,某个方向转动一定大小的角 ,图形的旋转,旋转中心,旋转角
16. A,B,C,D,E,C,D
17. (1),(3)
18. 将线段 绕点 逆时针旋转 ,再向左平移 个单位长度
19.
【解析】由题意可知,阴影部分的面积之和为 .
20. (1) 略.
(2) 有.
三角形 和三角形 关于直线 成轴对称.
21. 略
22. 略
23. (1) 图略.
(2) 全等.
因为 ,
所以 ,,
因为 ,,
所以 ,
所以 ,
即 ,
可证 .
(3) 直角三角形.
24. 如图:
同课章节目录
